中国库兹涅茨曲线的拐点何时出现？——基于基尼系数的预测

李绍东

(辽宁大学 工商管理学院，辽宁 沈阳 110036)

一、问题的提出

基尼系数(Gini coefficient)是用于判断一个国家或地区分配平等程度的指标，表示占人口总数一定百分比的社会成员所拥有的收入额在全部居民收入总额中所占的比重。基尼系数越低，说明分配平均程度越高，贫富差距越小；反之说明贫富差距越大。国际上通常把0.4作为收入分配贫富差距的“警戒线”，在0.4～0.5之间表示收入差距较大，在0.6以上表示收入差距悬殊。

中国自改革开放以来，随着收入渠道多元化、收入格局多样化以及改革的过程中对利益格局的重新调整，居民收入差距不断拉大。中国的基尼系数从世界银行2005年所估计的0.47上升到了2006年的0.496，2008年已经超过0.5，由此有人得出一个结论：中国的贫富分化状况已经踏越“警戒线”。中国的收入不平等会不会呈现库兹涅茨假说中先增大后减小的趋势？基尼系数开始下降的拐点在什么时间出现？成为我国当前社会经济领域的焦点问题。本文对中国1978年以来的收入不平等程度(基尼系数)与经济发展水平之间的关系进行了研究，以期验证库兹涅茨曲线的“倒U”假说，并预测其拐点出现的时间。

二、文献回顾

Kuznets(1955)最早提出，在经济发展的早期，由于只有少数具有技能或资本的人能够进入新的工业部门，收入不平等将会逐渐扩大；而在经济发展的后期，由于更多的人进入工业部门，农业工人稀缺性不断加剧，整个社会的收入不平等会逐渐缩小。

Kuznets的假说推动了大量经济学者对“倒U”型曲线进行统计检验。Acemoglu和Robinson(2002)通过对大量经济发达国家和发展中国家经济发展轨迹的考察，指出至少在两种情况下“倒U”型假说是不成立的：(1)始终保持低水平收入不平等和高速经济增长；(2)低的社会流动性导致高水平收入不平等和低速经济增长。李子奈等(1994)最早运用中国17个省份1991年的横截面数据对我国的人均GNP和基尼系数进行了拟合，验证了“倒U”形关系成立，但拟合效果较差，反映“倒U”形关系较弱。刘荣添等(2006)运用省际面板数据得出，全国及中西部地区的城乡收入差异与对数人均GDP存在“倒U”型关系,而东部地区为“正U”型关系。张世伟等(2007)应用两部门经济模型,模拟了中国经济发展过程中收入不平等的变动趋势，模拟结果显示:如果中国经济能够保持近年来的平均增长速度并且城乡内部收入不平等能够维持现有水平,则收入不平等水平将于2017—2020年间到达最大，即“倒U”型曲线拐点。

由于库兹涅茨仅仅通过一些数字的例子来阐述他的思想，一些经济学者尝试应用数理模型对“倒U”型假说进行形式化分析。Robinson (1976)率先对“倒U”型假说进行了形式化分析，他仅仅假设经济被分成两个不同收入水平的部门(传统部门和现代部门)，且随着时间的推移现代部门的人口比重单调递增。分析结果表明：“倒U”型假说能否成立仅仅取决于两部门收入水平的差异。但罗宾逊的分析局限在一个绝对不平等指标——收入对数方差，没有说明相对不平等指标(如基尼系数或泰尔指数等)随经济发展如何变动。针对罗宾逊模型，王检贵(2000)提出在两部门收入差距比较小的情况下“倒U”型假说不成立，但他的分析只具有数学意义而无经济意义，因为人口迁移的根本动力是现代部门和传统部门之间存在一定的收入差距。

三、理论分析与假设

库兹涅茨“倒U”曲线表明：在前工业文明向工业文明过渡的经济增长的早期阶段，尤其是在国民人均收入从最低上升到中等水平时，收入分配状况先趋于恶化，继而随着经济发展逐步改善，最后达到比较公平的收入分配状况，即长期变动轨迹呈倒“U”形状。该曲线揭示了人均收入与社会收入分配之间内在的基本规律，也显示了人均收入给社会分配机制带来的内在冲击与影响。

该曲线所表明的收入分配变化状况所依据的经验数据不多，有大量推测因素，故也被称为库兹涅茨“倒U假说”。库兹涅茨认为，收入差距变化是由当时一系列经济、政治、社会和人口条件造成的。在经济发展中存在着使收入不平等扩大的因素：一是储蓄和积累在少数高收入阶层的集中；二是工业化和城市化所引起的收入分配恶化，即农村与城市收入分配差距拉大。同时，还会出现一些抑制收入不平等因素，使收入分配不平等趋势逐步缓和，主要有：法律和行政干预、人口变动因素、产业结构调整因素以及“涓滴效应”。几十年来，库兹涅茨的“倒U曲线”假说经过许多经济学家的发展与完善，尽管没有被完全证实，但已经成为多数经济学家用来分析经济增长与收入分配二者之间关系及预测发展趋势的一种理论依据。

中国改革开放以来的经济发展历程基本上符合库兹涅茨的“倒U”曲线假说：随着我国工业化程度的提高以及更多的人进入工业部门和农业工人稀缺性的不断加剧，收入的不平等程度会逐渐缩小。而且中国目前的基尼系数已经接近0.5，远远高于警戒线，在未来不长时间段内，中国的库兹涅茨曲线应该会出现拐点，基尼系数出现下降趋势。所以本文提出两个假说来进行验证：

第一，拟合得到的中国的库兹涅茨曲线基本呈现出“倒U”的性质；

第二，中国的库兹涅茨曲线的拐点将在未来五年内出现。

四、模型构建与检验结果

(一)选择变量和模型的关系形式

1.确定模型的变量

本文试图运用中国的基尼系数和人均GDP的数据来检验库兹涅茨曲线的“倒U”性质，通过估计方程预测中国库兹涅茨曲线的拐点，所以模型以基尼系数作为被解释变量(GINI)，以人均GDP作为解释变量(PGDP)来估计方程。

2.确定模型的数学形式和参数范围

由于库兹涅茨曲线的“倒U”性质，结合我国基尼系数与人均GDP 的散点图与X-Y曲线图(见图1和图2)，本文对库兹涅茨曲线的拟合使用一元二次方程的形式：

模型中，为保证基尼系数存在最大值，故要求β2<0；ut为随机误差项，描述变量之外的因素对模型的干扰。

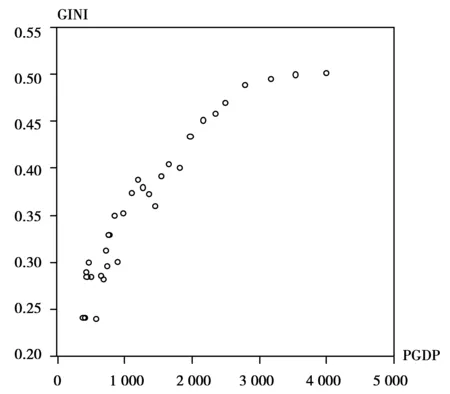
图1 我国1978—2008年与人均GDP散点图基尼系数

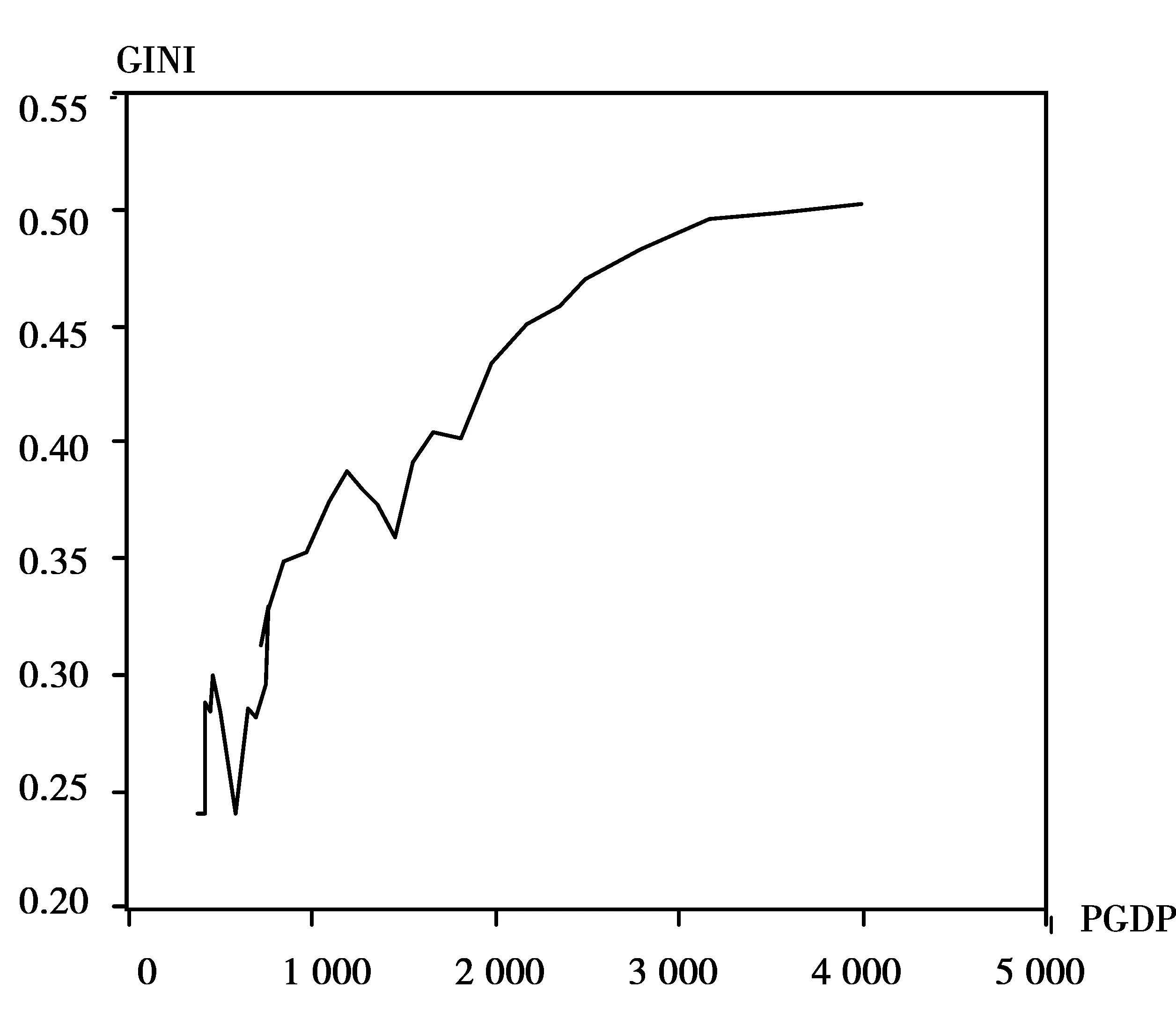
图2 我国1978—2008年基尼系数与人均GDP的X-Y曲线图

(二)样本数据收集

本文所用的1978—2007年的人均GDP数据来源于《中国统计年鉴2008》，2008年的人均GDP数据根据国家统计局公布的数据计算得到，所有人均GDP数据都以1978年为基期进行了价格指数调整。

国外经济理论文献中对基尼系数的估算一般遵循两种途径：一是利用分户数据直接估计收入分配的密度函数从而估算基尼系数,二是利用分组数据估计洛伦兹曲线,然后再估算基尼系数。由于我国统计部门的城乡收入分配调查的分户数据不对外公开,而许多学者计算基尼系数所采用的公式和分组数据不同，导致目前对中国基尼系数的计算及预测结果差别较大。在参考了世界银行的基尼系数数据及各方学者的观点之后，本文1978—2004年的基尼系数来源于尹成远(2008)；2005—2007年的数据来源于世界银行的《人类发展报告》及中国社会科学院《中国社会发展年度报告》；2008年的基尼系数来源于张焕波、王铮(2007)的预测数据(见表1)。

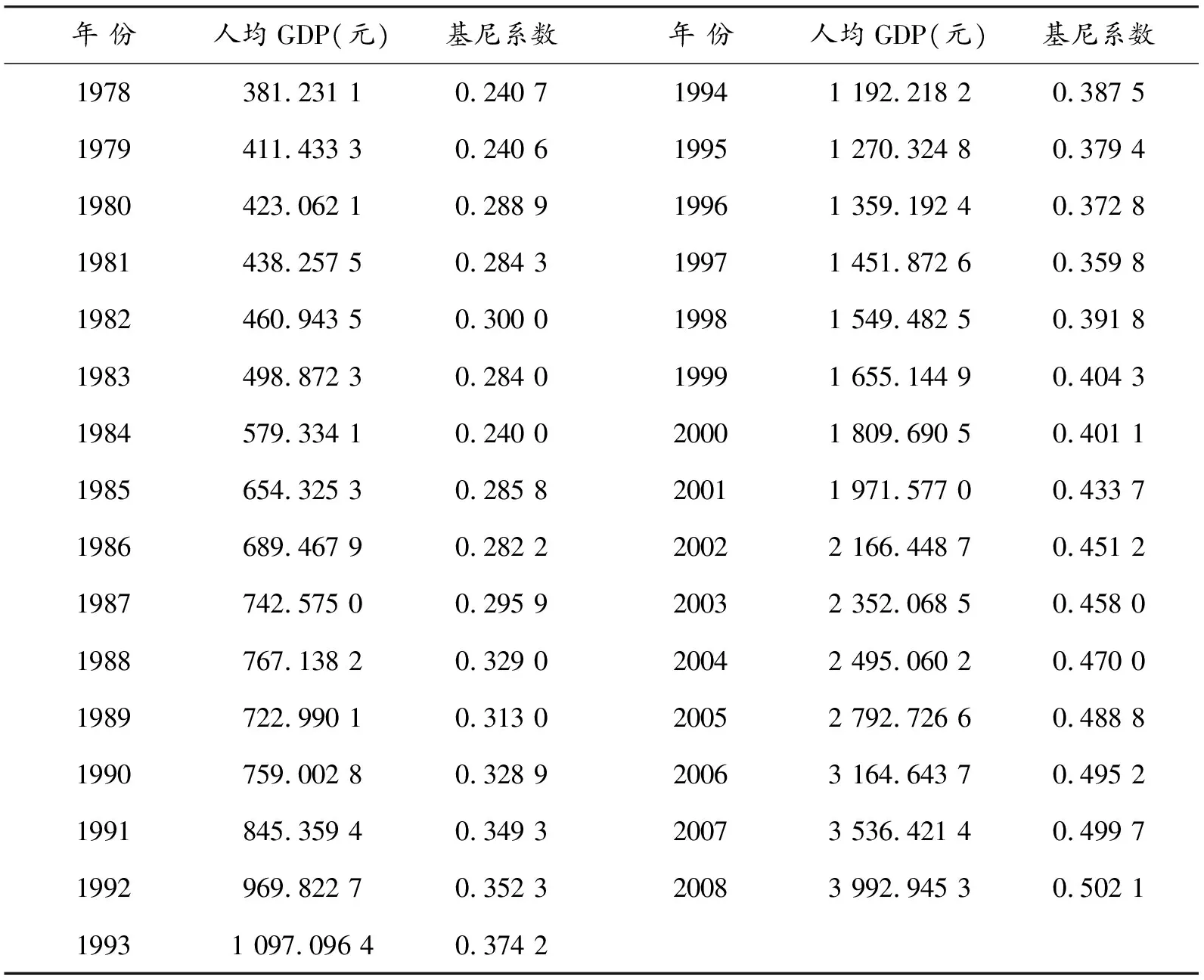
表1 中国基尼系数与调整后的人均GDP数据表(1978—2008)

(三)参数估计与检验

用OLS方法估计，得到如下回归方程：

GINI=0.205+1.57×10-4PGDP-2.07×10-8

PGDP2

(20.04) (11.61) (-6.08)

R2=0.95 DW=1.12 F=269.1

1.经济意义检验

由回归结果可以看出，二次方项的系数为负，拟合曲线呈现出良好的库兹涅茨“倒U”曲线的性质。

2.拟合优度检验

由R2=0.95及调整后的R2=0.947，说明模型对样本数据有很高的拟合优度。

3.方程显著性检验

变量数k=2，样本容量n=31，给定显著水平α=0.01，查F分布表中自由度为28、α=0.01的临界值，得到F0.01(2,28)=5.39。F=269.1>F0.01(2,28)=5.39，因此模型中被解释变量基尼系数与人均GDP、人均GDP二次方的线性关系在99%水平下显著成立。

4.变量显著性检验

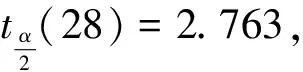
5.序列相关检验

根据显著性水平5%，样本容量31和解释变量数k=2，查D.W.分布表，得到dl=1.30,du=1.57。计算得到的D.W.值为1.12，0

下面采用LM统计量进行二阶滞后序列相关检验(p=2)，得到结果如下：

F-statistic2.984 329Prob. F(2,26)0.068 1Obs∗R-squared5.6753 91Prob. Chi-Square(2)0.058 6

LM统计量显示，在5%的显著性水平下接受原假设，回归方程的残差序列不存在二阶滞后序列相关。

本文采用AR(1)来修正回归方程残差序列的自相关性：

回归估计的结果如下：

由一阶差分模型的回归结果可以看出，虽然D.W.值稍有增大，但差分方程系数的t统计量很小，在95%的水平上显著等于0，未通过变量显著性检验。AR(1)模型对修正方程随机误差项的序列相关不起作用，所以本文对库兹涅茨曲线的拟合仍采用原回归结果。

本文通过其他方法来改善回归方程中随机误差项的序列相关问题，但效果都不明显，主要原因是方程本身忽略了影响基尼系数的其他变量。人均GDP只是影响作为衡量收入平等程度指标的基尼系数的一个变量。李宏毅,邹恒甫(1998)认为决定收入分配不平等的因素主要是教育水平、财富分配、金融发展和民主自由的程度。王小鲁,樊纲(2005)也指出经济增长、收入再分配、社会保障、公共产品、基础设施和制度对中国的收入差距有重要的作用。所以本文中出现的序列相关难以修正的问题可以理解为是由于省略了显著的解释变量而引起的虚假序列相关。但就本文仅仅试图拟合基尼系数与经济发展水平的库兹涅茨曲线来说，回归结果已经能够满足要求。

6.库兹涅茨曲线的拐点预测

由样本数据拟合的库兹涅茨曲线为：

通过求解基尼系数最大化的一阶条件可以求出，当人均GDP达到3 792.27元的时候，基尼系数达到最大值，为0.503。结合表1的基尼系数与调整后的人均GDP数据，并考虑到本文中基尼系数的准确性以及由于忽略变量导致的虚假序列相关的误差，可以预测，中国库兹涅茨曲线的拐点大致会在2010—2015年这个时间段内出现。

五、结论与启示

(一)主要结论

通过对中国库兹涅茨曲线的拟合结果可以看出，中国的库兹涅茨曲线很好地呈现出了“倒U”曲线的性质，衡量收入不平等程度的基尼系数呈现先上升后下降的趋势。这与大多数学者通过时间序列数据和横截面数据得到的结论基本一致。根据本文拟合的库兹涅茨曲线计算，并考虑回归模型的虚假序列相关的问题以及基尼系数的误差，得出中国基尼系数下降的拐点在2010年—2015年这个时间段内出现。这与某些学者提出的中国库兹涅茨曲线的拐点不会在2015年之前出现而大致出现于2020年的结论有所差异。

(二)启示

中国基尼系数的计算受收入统计资料的限制，除货币收入外各项实物收入难以统计，特别是农民用于自给自足的实物难以统计，导致各种对基尼系数的计算结果产生较大偏差，所以依据基尼系数进行的收入不平等的研究结论只能作为一定程度上参考的依据。

反映一个国家或一个地区经济发展水平的变量除了人均GDP还有很多其他的变量，而忽略这些变量会对库兹涅茨曲线的拟合产生偏差。所以本文仅以基尼系数和人均GDP数据对库兹涅茨曲线的拟合的准确性还有待提高，但计算出的拐点还是具有一定的参考价值。

中国的特殊经济发展背景和阶段使我们对基尼系数理论在中国的适用性产生质疑,是不是可以根据基尼系数大于0.4这个国际公认的警戒线来评价中国的收入不平等状况?中国对于收入不平等程度的承受能力到底有多大?要准确回答这些问题,需要对基尼系数理论背后隐藏的内容进行分析,并结合中国的现实作出正确判断。

[参考文献]

[1] Kuznets S. Economic Growth and Income Inequality[J]. American Economic Review, 1955, 45: 1-28.

[2] Acemoglu D, Robinson J. The Political Economy of the Kuznets Curve[J]. Review of Development Economics, 2002(6): 183-203.

[3] 李子奈,田一奔,羊健.居民收入差距与经济发展水平之间的关系分析[J].清华大学学报(哲学社会科学版),1995(1):35-41.

[4] 刘荣添,叶民强.中国城乡收入差异的库兹涅茨曲线研究——基于各省份面板数据(1978—2004年)的实证分析[J].经济问题探索,2006(6):9-13.

[5] 张世伟,吕世斌,赵亮.库兹涅茨“倒U”型假说:基于基尼系数的分析途径[J].经济评论, 2007,(4):40-45.

[6] Robinson S. A Note on the U Hypothesis Relating Income Inequality and Economic Development [J]. American Economic Review, 1976, 66: 437-440.

[7] 王检贵.“倒U”现象是不是一条经济法则?——对罗宾逊经典结论的质疑[J].经济研究,2000(7):63-67.

[8] 尹成远，赵桂玲,周稳海.中国人身保险保费收入的实证分析与预测研究[J],保险研究，2008(1):48-52.

[9] 王小鲁,樊纲.中国收入差距的走势和影响因素分析[J].经济研究,2005，40(10):12-18.

[10] Li H, Zou H F.Income Inequality is not Harmful for Growth:Theory and evidence[J]. Review of Development Economics, 1998, 2(3): 318-334.