材料的各向异性对渗流场的影响分析
胡 瑞 曾 胜
(湖南五凌电力工程有限公司,长沙 415000)
在土石坝的设计中,材料渗透参数的选取是坝体的防渗设计的重要部分,它对坝的渗透稳定起着至关重要的作用[1].同时,在水利工程建设中,各向异性渗流问题愈来愈受到关注,如在各向异性材料的土坝内会带来坝体内水头压力、浸润线抬高、在坝下游的出渗坡降增大等现象,相对于各向同性渗流场而言其危害性更大[2-4].利用数值模拟方法计算堤坝工程的非饱和区渗流,并在材料各向异性的基础上进一步研究非饱和区渗流作用下堤坝自由面变化情况,为堤坝非饱和区渗流在工程上的应用提供参考.
1 非饱和土的渗流方程
在饱和土壤中,引起水分转移的力是重力和水的压力,在非饱和土中,支配着土壤水在液态下整体转移的是重力和水的表面张力,Richards等曾在1931年就证明非饱和土中的渗流与饱和土一样符合达西定律和连续方程.若将达西定律代入连续方程(忽略渗透过程中总应力的改变和土颗粒骨架的变形)并以总水头h作为未知量,当渗透的主方向与坐标轴一致时,非饱和土渗流的二维微分方程就可表示为

式中,kx,ky分别为x和y方向上的渗透系数;θw为体积含水率;h为总水头;t为时间.
令y为位置水头,则h=uw/γw+y.
若mw为土水特征曲线的斜率,则 ∂θw=mw∂uw=mwγw∂(h-y),式(1)就可以写为
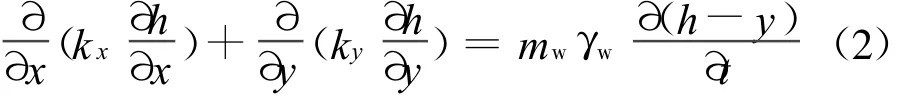
由于y是常数,式(2)简化为
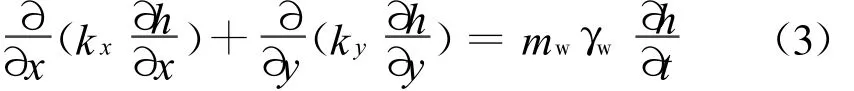

从式(4)也可以看出非饱和土中的渗透系数k不再是常数,而是含水量的一个函数,此函数被称为非饱和土的渗透系数函数.
因此,要进行渗流分析“需具备以下基本条件: (1)材料的渗透系数函数;(2)确定边界条件.当上述条件已知时,就可以对以上方程进行求解,从而得到非饱和土渗流场.
2 土坝饱和-非饱和渗流分析
2.1 计算模型[5]
某均质土坝,坝高50 m,顶宽10 m,上游坝坡为1∶2.5,下游坝坡为1∶2,上游水位为45 m,下游水位为5m,渗透系数为0.29m/d,孔隙率为0.464.大坝的模型如图1所示,分2091个节点,2000个四边形单元.
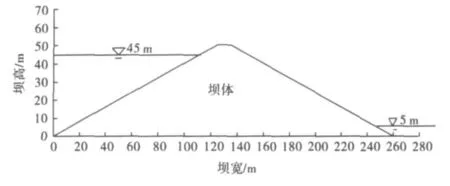
图1 土坝计算模型图
2.2 计算工况的选取
考虑非饱和区材料渗透系数各向异性,分别以不同的水库水位下降速度来进行渗流计算分析,其工况组合见表1~2.

表1 工况计算表
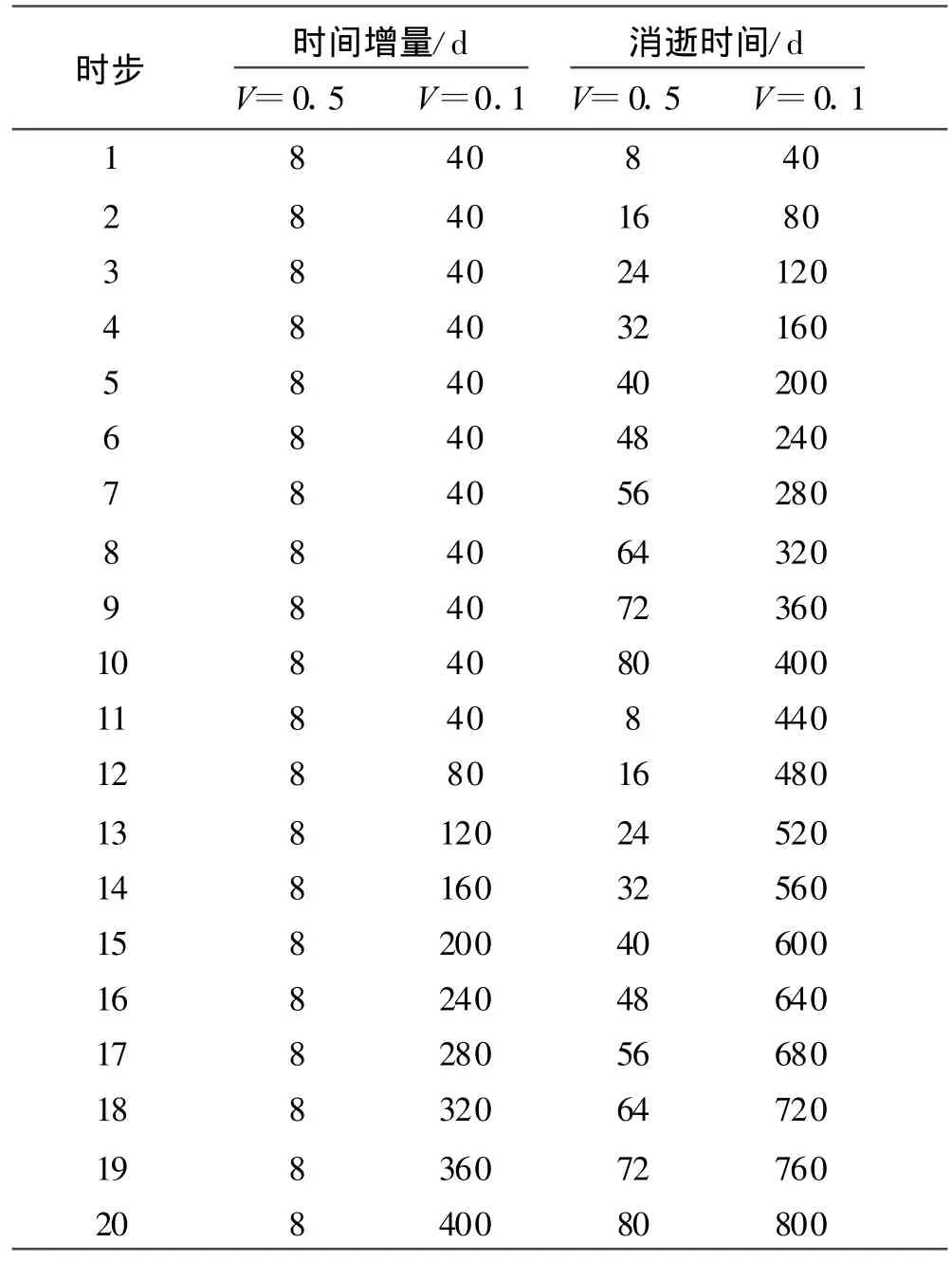
表2 非稳定渗流计算时步表
2.2.1 稳定渗流计算结果分析
由于非饱和区的存在,浸润线附近的饱和区的渗流水会穿过浸润线而进入非饱和区;增加水平方向的渗透系数,更多的水流向下游,负压区逐渐减小,等势线向下游推移,如图2~4所示.
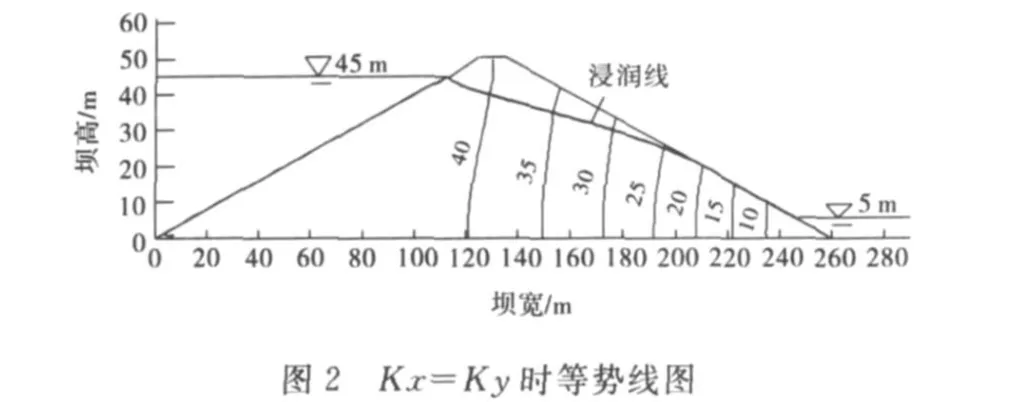
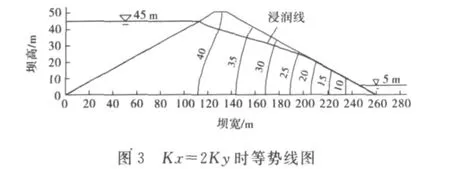
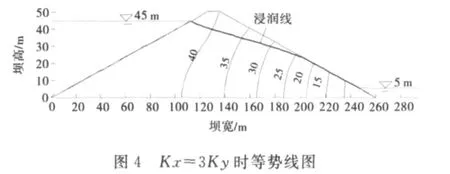
从表3可以看出,随着水平渗透系数的增加,更多的水向下游渗流,逸出点略有抬升,意味着浸润线抬升,渗流量明显增大,说明材料的各向异性对其影响较大.

表3 稳定渗流计算结果对照表
2.2.2 非稳定渗流计算结果
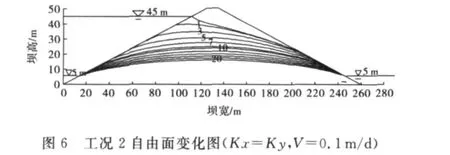
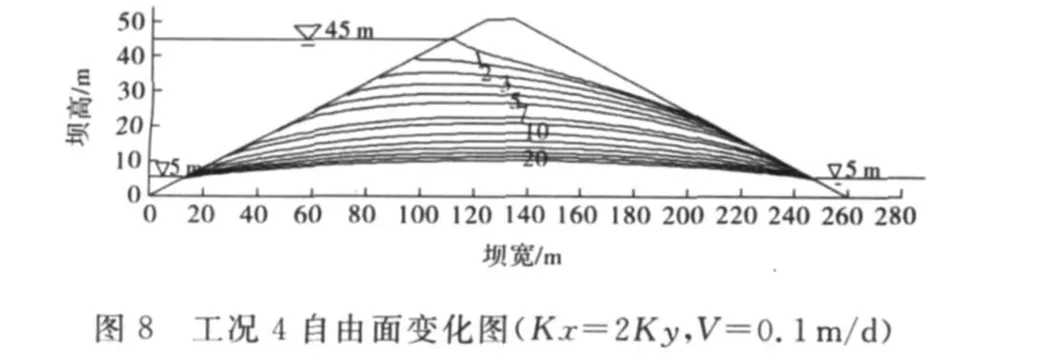
图5~10可以看出(图中的数字为时步数),库水位下降浸润线也下降,当不考虑材料的各向异性时,水位迅速下降,坝内的孔隙水压力来不急消散,自由面的形状较陡,同时在坝的上游面形成严重的“倒流”现象,这将影响上游坝坡稳定(如图5所示).在同一下降速度时,随着水平渗透系数的增加,自由面的形状由陡逐渐趋于平缓,变化较为显著,说明坝内的孔隙水压力消散迅速,下降形成的水“倒流”现象不严重.尤其是工况5和工况6时,由于水平渗透系数较大,在水库下降速度较快(V=0.5m/d)时,其坝内自由面变价也较为平缓,对上游坝坡的稳定性影响不大,说明材料的各向异性对渗流场的影响较为显著.




3 结 语
由于非饱和区的存在,流水会穿过浸润线而进入非饱和区,坝内非饱和区域也存在渗流.在渗透参数的各向异性的条件下,随着水平渗透系数的增加,渗透坡降变化不大,而单宽流量增大较明显;在非稳定渗流中,即使水库水位快速下降,坝内的孔隙水压力也能迅速消散,自由面变化也较显著,其对上游坝坡稳定产生的影响比不考虑材料各向异性时的要小,说明渗透参数的各向异性对其影响较大.单宽流量的增大,在保证渗透稳定的条件下可根据兴利的要求来选取排水设施,但它也会给下游坝坡带来影响;水库降落时,孔隙水压力的消散迅速,它同时也给上游坝坡带来安全隐患,对坝体的渗透稳定也同样存在着影响,故都应做好防渗排水措施.而实际工程中,存在着土体非饱和性、不均匀性、材料各向异性的特点,所以对材料渗透参数的各向异性在非饱和条件下来进行渗流分析较为合理、更为贴近工程实际.
[1] 韩 瑜,李松德.土石坝心墙内浸润线的逸出高度[J].西安理工大学学报,2000(2):204-206.
[2] 毛昶熙.渗流计算分析与计算[M].北京:水利电力出版社,1990:62-68.
[3] 张家发.土坝饱和与非饱和稳定渗流场的有限元分析[J].长江科学院院报,1994(9):41-45.
[4] 刘晓庆.高土石坝稳定-非稳定渗流有限元分析[J].三峡大学学报:自然科学版,2008,30(3):30-33.
[5] 王晓章.非稳定渗流及其作用下的边坡稳定数值模拟[D].西安:西安理工大学,2004:62-68.

