基于数字图像的水果分形维数特征

温芝元

（湖南农业大学 理学院，湖南 长沙 410128）

橘、橙和苹果等水果虽外形都呈仿球形，但量化的形状特征值有所不同，即使是同一种水果，这种差异同样存在，描述这种差异对品种的自动识别与同品种的等级规格判定十分重要．人们很早就发现许多不规则图形的面积与周长间存在某种对应关系[1-6]．曹乐平等[7-9]以分形维数为指标，对柑橘形状与光滑度进行机器视觉分级，效果较好；以周长、面积和分形维数为柑橘品种的特征值，利用小波神经网络识别宫川温州蜜柑、脐橙朋娜和泸溪无核椪柑，正确识别率分别为 95%、95%、97.5%，总正确识别率为95.83%；将柑橘色调进行分区，提取各区域色调分形维数，以BP神经网络为映射器，无损检测宫川温州蜜柑糖度及有效酸度，在±1.5°Brix内，糖度的正确识别率为66.617 5%，在±0.5°Brix内，有效酸度的正确识别率为73.927 5%．笔者对橘、橙和苹果的数字图像进行分析与处理，计算其侧面与花萼面的分形维数，研究这3种仿球形水果的自相似性，旨在为水果品种的识别及外形质量等级分级提供理论依据．

1 材料与方法

1.1 材 料

温州蜜柑20个，麻阳冰糖橙17个，红富士苹果18个，均购自长沙红星水果市场．

1.2 机器视觉系统与数据分析软件

机器视觉系统：光箱（500 mm×500 mm×500 mm，白色背景）、光源（在光箱顶部，关于相机镜头对称，安装 4盏 11 W 节能灯）、相机（Olympus C-5000Z，500万有效像素，分辨率TIFF2560×1 920，镜头 7.8～23.4 mm，焦距 0.5 m～∞，快门速度1/1000～16 s，光圈F/2.8～F/4.8，镜头距光箱底距离468 mm）、计算机（Lenovo P Ⅳ 2 . 13 G，内存512 M，Windows Xp操作系统）．

数据分析软件为Matlab 7.1．

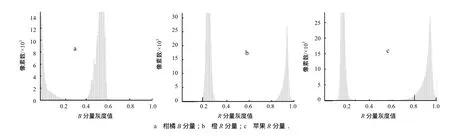
图1 颜色分量直方图Fig.1 Colour component histogram

1.3 方 法

1.3.1 图像处理

将水果依次置于光箱中．每果采集花萼面和侧面图像各1幅．

（1） 图像裁切．一幅M×N的RGB图像可以用M×N×3的矩阵描述．图像中的每一个像素点对应于红（R）、绿（G）、蓝（B）3个分量组成的3元组．定义图像裁切窗口：

（2） 图像二值化．将水果的 RGB图像转换为double类型，分别作柑橘图像蓝色（B）分量直方图（图 1-a），橙和苹果红色（R）分量直方图（图 1-b、图1-c）．由图1可见，3个直方图均呈明显的双峰分布，分别对应水果区域和背景．

由图2确定3种水果颜色分量阈值T，并对柑图像作如下变换：

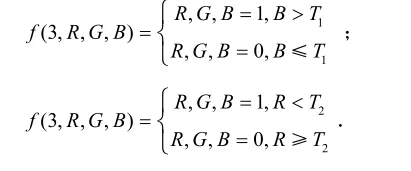
式中，1T为柑橘图像的颜色分量阈值，2T为橙和苹果图像的颜色分量阈值．通过以上变换，图像中，水果区域R、G、B均为1，水果区域外R、G、B均为0，图像转化成黑、白两级灰度图像．设置0与1间的任意阈值，将灰度图像转化成黑、白二值化图像（图2-d）．与迭代法二值化图像（图2-b）和Otsu法二值化图像（图2-c）相比，用这种方法得到图像的边界清晰、精确，水果区域内不存在孔眼，去背景彻底．

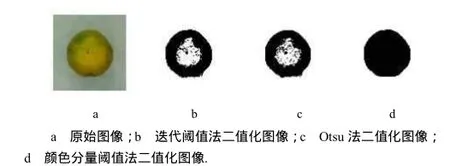
图2 二值化图像Fig.2 Binary image comparison

通过四连通法边界跟踪，将二值化后的水果图像形成封闭的水果轮廓边界，但多像素的边界线影响图像中水果区域周长的计算，所以，再将边界线细化为单像素，并保持原边界的连通性，从而提高周长计量的精度．

（3） 编写 3种水果分形维数 Matlab计算程序．图3为柑橘分形维数计算程序框图，橙和苹果的分形维数计算程序框图与之类似．

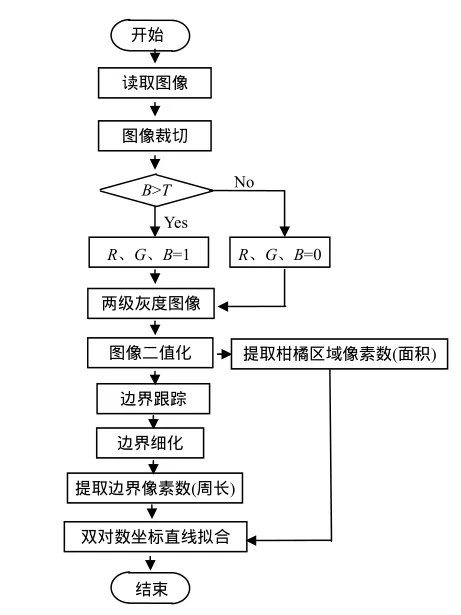
图3 柑橘分形维数计算程序框图Fig. 3 Citrus block diagram of fractal dimension calculation

1.3.2 分形维数的计算

对于自然界中岛屿等非规则图形，Hentschel等[10]证明了其周长P与面积A的关系：0.5D PA∝ ．式中，D为分形维数．对于水果数字图像，

2 结果与分析

2.1 同一种水果的分形维数（以柑橘为例）

根据式（2），计算出3种水果2个方向的分形维数如表1．

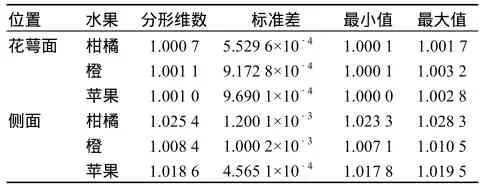
表1 3种水果花萼面和侧面的分形维数Table 1 Fractal dimensions of calyx and profile of 3 kinds of fruits

从表1可知，柑橘花萼面分形维数的标准差小，说明柑橘花萼面分形维数差异不明显；图4中柑橘花萼面周长-面积双对数坐标拟合直线的拟合度较高，这主要是因为柑橘花萼面图像都呈准圆形．

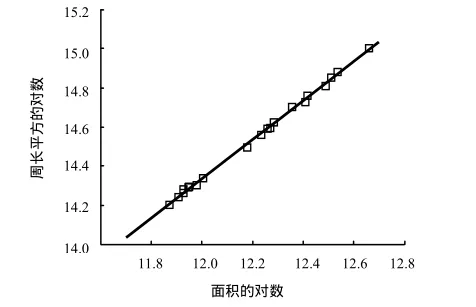
图4 柑橘花萼面周长-面积双对数拟合直线Fig.4 Citrus calyx fitting line based on perimeter-area logarithm

从表1可知，柑橘侧面分形维数的标准差较大；由图5可知，柑橘侧面周长-面积双对数拟合直线的拟合度较低，说明柑橘侧面分形维数差异明显．

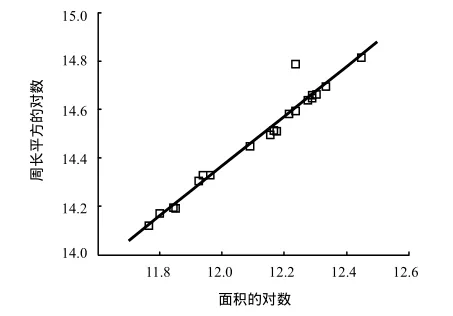
图5 柑橘侧面周长-面积双对数坐标拟合直线Fig.5 Citrus profile fitting line based on perimeter-area logarithm

比较柑橘花萼面和侧面2个方向的分形维数，花萼面的分形维数比侧面的分形维数小．

橙和苹果的情况与柑橘类似．

2.2 同一种水果分形维数的方差分析（以橙为例）

橙的花萼面和侧面2个方向分形维数的3种方差列于表2．表2中，F值远大于临界值，表明橙在2个方向的分形维数差异明显，不能用一个方向的分形维数代替另一个方向的分形维数，评判仿球形水果分形维数至少要从含侧面在内的2个方向度量．

柑橘和苹果的情况与橙类似．

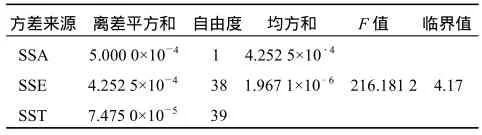
表2 橙花萼面和侧面分形维数的方差分析Table 2 Anova of calyx/profile fractal dimension of orange

2.3 3种水果分形维数的方差分析

由表3可见，3种水果花萼面分形维数的F值小于临界值，侧面分形维数的F值远大于临界值；由图6 可知，图6-a数据点拟合度较高，图6-b数据点拟合度较低，这表明柑橘、橙及苹果花萼面的分形维数差异不明显，但侧面分形维数差异明显，故可用其中任一种水果花萼面的分形维数近似代替另外2种水果在该方向上的分形维数；用其中某一种水果侧面的分形维数代替另外2种水果该方向上的分形维数，则是一种粗略的估计，因此，水果侧面的分形维数是识别仿球形水果种类的关键，也是判定同一种水果表面轮廓是否圆整、光滑等外形质量等级的重要参数．这一点有别于王艳平等[11]对番茄生理病害果的识别．

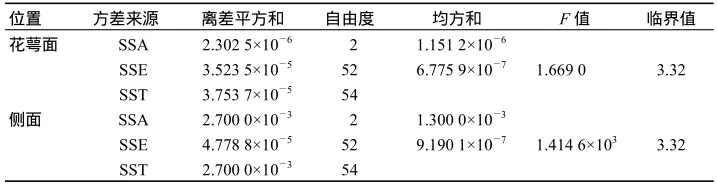
表3 3种水果分形维数的方差分析Table 3 Anova of fractal dimension of 3 kinds of fruits

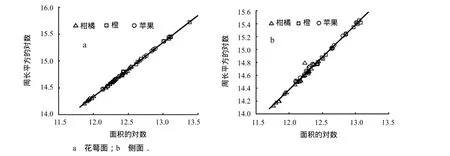
图6 3种水果周长-面积双对数拟合直线Fig.6 Fitting line of 3 kinds of fruits based on perimeter-area logarithm

3 结论与讨论

用本研究中设计的程序进行仿球形水果图像分析与处理，不仅水果轮廓清晰，无孔眼，而且用周长-面积法计算出的水果的分形维数精度较高．大小不一的同种水果，其同一方向的分形维数差异较小，一方面表明水果具有明显的自相似性，可以通过计算机来模拟其生长过程．利用水果花萼面与侧面2个方向分形维数的差异，以水果花萼面与侧面2个方向的分形维数为参数，可对水果外形、质量等级等进行机器分级．因本试验以色泽鲜艳的成熟水果为对象，在特定的光箱中进行图像采集，光箱背景与水果色差明显，用基于颜色分量的阈值方法，去除图像背景后提取的水果区域轮廓清晰、光滑，但生长中水果色泽与树叶接近，通过颜色分量去背景会存在误检与漏检，所以，所提取的分形维数误差大．以自然场景中的挂果为对象，找出生长过程中水果的分形维数特征分布，将是后续研究的重点．

[1] Attila R Imre．Artificial fractal dimension obtained by using perimeter–area relationship on digitalized images [J]．Applied Mathematics and Computation，2006，173：902-915．

[2] Andreas Krein，Ellen Petticrew，Thomas Udelhoven．The use of fine sediment fractal dimensions and colour to determine sediment sources in a small watershed [J]．Catena，2003，53：165-179．

[3] Jin-Ju Park，Su-Il Pyun．Pit formation and growth of alloy 600 in Cl-ion-containing thiosulphate solution at temperatures 298～573 K using fractal geometry [J]．Corrosion Science，2003，45：995-1010．

[4] Gyoung-Ja Lee，Su-Il Pyun，Chang-Kyu Rhee．A study on electrophoretic deposition of Ni nanoparticles on pitted Ni alloy 600 with surface fractality[J]．Journal of Colloid and Interface Science，2007，308：413-420．

[5] Seung-Bok Lee，Su-Il Pyun．Determination of the morphology of surface groups formed and PVDF-binder materials dispersed on graphite composite electrodes in terms of fractal geometry[J]．Journal of Electroanalytical Chemistry，2003，556：75-82．

[6] Su-Il Pyun，Chang-Kyu Rhee．An investigation of fractal characteristics of mesoporous carbon electrodes with various pore structures[J]．Electrochimica Acta，2004，49：4171-4180．

[7] 曹乐平，温芝元，陈理渊．基于分形维数的柑橘形状与光滑度的机器视觉分级[J]．测试技术学报， 2009，23（5）：407-411．

[8] 曹乐平．基于周长面积分形维数的柑橘品种机器识别[J]．农业工程学报，2010，26（2）：351-355．

[9] 曹乐平，温芝元，沈陆民．基于色调分形维数的柑橘糖度和有效酸度检测[J]．农业机械学报，2010，41（3）：143-148．

[10] H G E Hentschel，Itamar Procaccia．The infinite number of generalized dimensions of fractals and strange attractors[J]． Nonlinear Phenomena： Physica D，1983，8（3）：435-444．

[11] 王艳平，戴小鹏，黄璜．基于数学形态学和神经网络对番茄生理病害果的识别[J]．湖南农业大学学报：自然科学版，2006，32（3）：344-346．

英文编辑：罗文翠