舰船燃气涡轮叶片三维热流固耦合应力应变分析及寿命预测

朱江江 杨自春

海军工程大学船舶与动力学院，湖北武汉 430033

舰船燃气涡轮叶片三维热流固耦合应力应变分析及寿命预测

朱江江 杨自春

海军工程大学船舶与动力学院，湖北武汉 430033

为提高燃气轮机的可靠性、可用性以及可维护性而进行的寿命预估与减损控制研究，需要对燃气轮机的关键零部件进行结构特性分析。对舰船燃气轮机涡轮叶片在紧急升工况载荷谱下的应力应变状态进行了三维热流固耦合有限元分析，针对典型载荷谱计算了涡轮叶片应力应变的变化规律，对涡轮叶片材料进行了控制应变试验，为叶片寿命预测提供了必要的参数。根据应力应变分析结果利用Basquin公式和Manson－Coffin公式计算了2个危险点处的疲劳裂纹起始寿命。并根据分析结果对涡轮叶片进行了寿命预测，预测结果可以作为燃气轮机使用维修的参考依据。

燃气涡轮叶片；热流固耦合；应变试验；疲劳寿命；裂纹

1 引言

为了提高燃气轮机的可靠性、可用性以及可维护性而进行的寿命预估与减损控制研究，需要对燃气轮机的关键零部件进行结构特性分析［1］。燃气轮机涡轮叶片是燃气轮机的关键部件之一，承担着把燃气工质热能转化为机械能的重要任务。涡轮叶片在运行中不仅承受着离心力、热应力及稳定气流力的共同作用，还受到高温环境和腐蚀介质的影响。据不完全统计，我国航空燃气轮机以往发生各类断裂失效中转动部件的失效高达80%［2］以上。涡轮叶片失效通常可以分为两类：低周疲劳失效［3］和蠕变断裂［4］。 本文对某型舰船燃气轮机涡轮叶片在紧急升工况载荷谱下的应力应变状态进行了三维热流固耦合有限元分析，并根据分析结果对涡轮叶片进行了寿命预测，预测结果可以作为燃气轮机使用维修的参考依据。

2 典型载荷谱

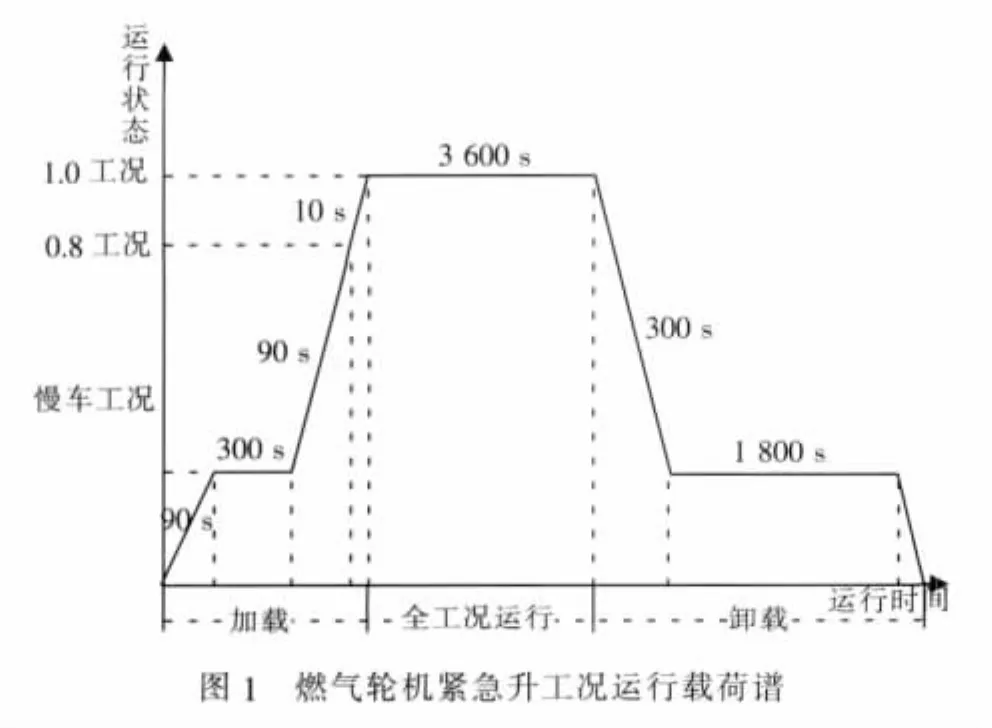
本文以燃气轮机紧急升工况运行载荷谱为有限元分析的边界条件。因为紧急升工况载荷谱是对燃气轮机损耗最大的载荷谱，所以在该载荷谱下得到的预测寿命结果是实际使用寿命的下限。根据燃气轮机工作程序要求，由冷态至0.8名义工况紧急发出功率时间应不少于9.5 min。3 min发动机启动，首先接通起动电机，90 s燃烧室燃油点火，180 s发动机进入慢车；5 min在慢车工况暖机，由慢车到名义工况正常发出功率的时间应少于5 min，即慢车到名义工况的时间在1.5～5 min之间；由名义工况降到慢车的正常时间不少于5 min。为了冷却燃气轮机，在慢车工况下，转动30 min时间。另假设燃气轮机进入0.8工况后迅速上升到全工况运行用时10 s，然后在全工况状态下运行1 h。图1所示为燃气轮机紧急升工况运行载荷谱。

3 燃气涡轮叶片热弹塑性应力应变分析

由于涡轮叶片运行过程中的应变问题属于小变形问题，叶片变形对周围的流场、温度场的影响较小，所以本文采用单向热—流—固方法对燃气涡轮叶片进行三维应力应变分析。

3.1 燃气涡轮叶片流场CFD分析

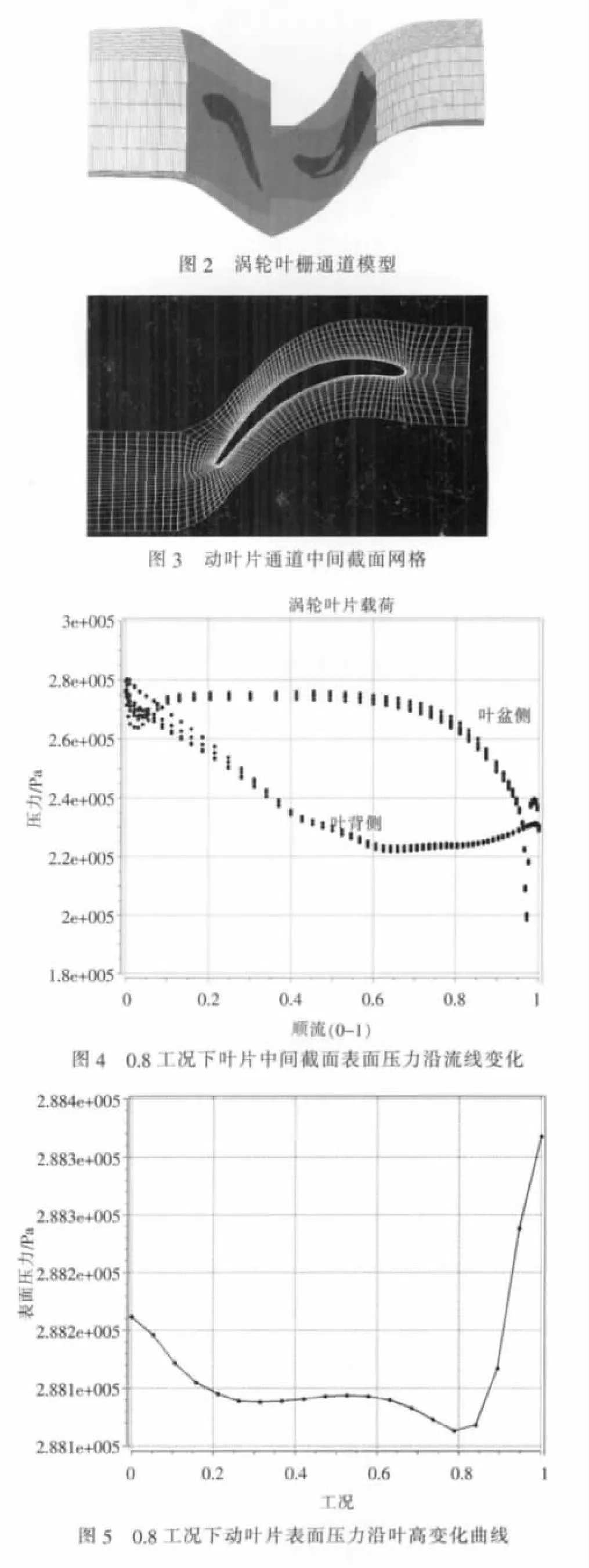
本文使用大型有限元软件中的ANSYS－CFX模块对燃气涡轮导向叶片与动叶片的实体及叶栅通道进行全尺寸建模，整个流场区域模型如图2所示。流体区域采用有限体积法进行区域离散，采用H－J－O混合网格进行网格划分，如图3所示。模型的边界条件为入口设置总压和总温，出口设置静压，压力值采用绝对压力。湍流模型采用 kε模型。图4、图5所示为0.8工况下动叶片表面压力计算结果。从图中可以看出叶片进气边的压力最大为2.8e＋5 Pa，叶盆侧与叶背侧压力变化曲线形式不同对叶片形成气流力，造成承受叶片由叶盆侧向叶背侧的弯曲应力。而压力沿叶高方向变化不大，图中叶顶处压力升高的原因是叶片与机匣存在间隙。

3.2 涡轮叶片瞬态温度场分析

当燃气轮机变工况工作时，涡轮盘片系统的温度也会发生变化。温度的变化会导致叶片产生3种不同类型的损伤：温度变化滞后性产生的热应力；高温时材料物性参数降低导致局部高应力区域发生塑性变形；温度超过材料0.5倍熔点时材料发生永久蠕变变形。

在ANSYS结构分析模块中建立涡轮盘片系统有限元模型如图6所示，温度单元采用可以进行热结构转换的SOLID70三维8节点热单元。热边界条件为对流换热，叶片与轮盘之间为接触传热按图1.1所示载荷谱进行加载分析。图7、图8所示为温度场计算结果。从图中可以看出危险点14924与11045（危险点的确定见图9）相比温度有滞后性。

3.3 涡轮盘片系统瞬态应力应变分析

涡轮叶片在恶劣的运行条件下经受离心力、热应力和气流力的综合作用，所经历复杂的应力和应变直接决定其运行寿命。本节综合前两节流场分析与温度分析的结果得到涡轮叶片复杂环境下的瞬态应力应变。

涡轮盘片系统结构分析的几何模型与温度分析时相同，只需把单元类型从温度单元SOLID70转换为结构单元SOLID183，同时建立涡轮叶片轮盘结构单元接触表面。离心力载荷通过设置旋转角速度加载，温度载荷作为体载荷加载到单元中，压力载荷作为面载荷加载到涡轮叶片叶身表面。限制有限元模型的刚体位移，叶片与轮盘接触表面设置为非线性摩擦接触，同时限制叶根沿榫槽方向的位移。叶片材料塑性变形与蠕变交互作用的模拟采用双线性随动强化模型与时间硬化蠕变本构模型组合。按图1所示紧急升工况载荷谱加载，图9～图13为应力应变计算结果。

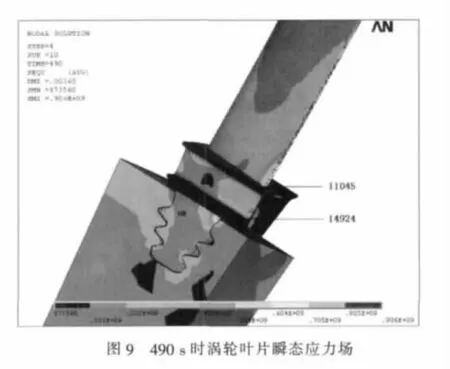
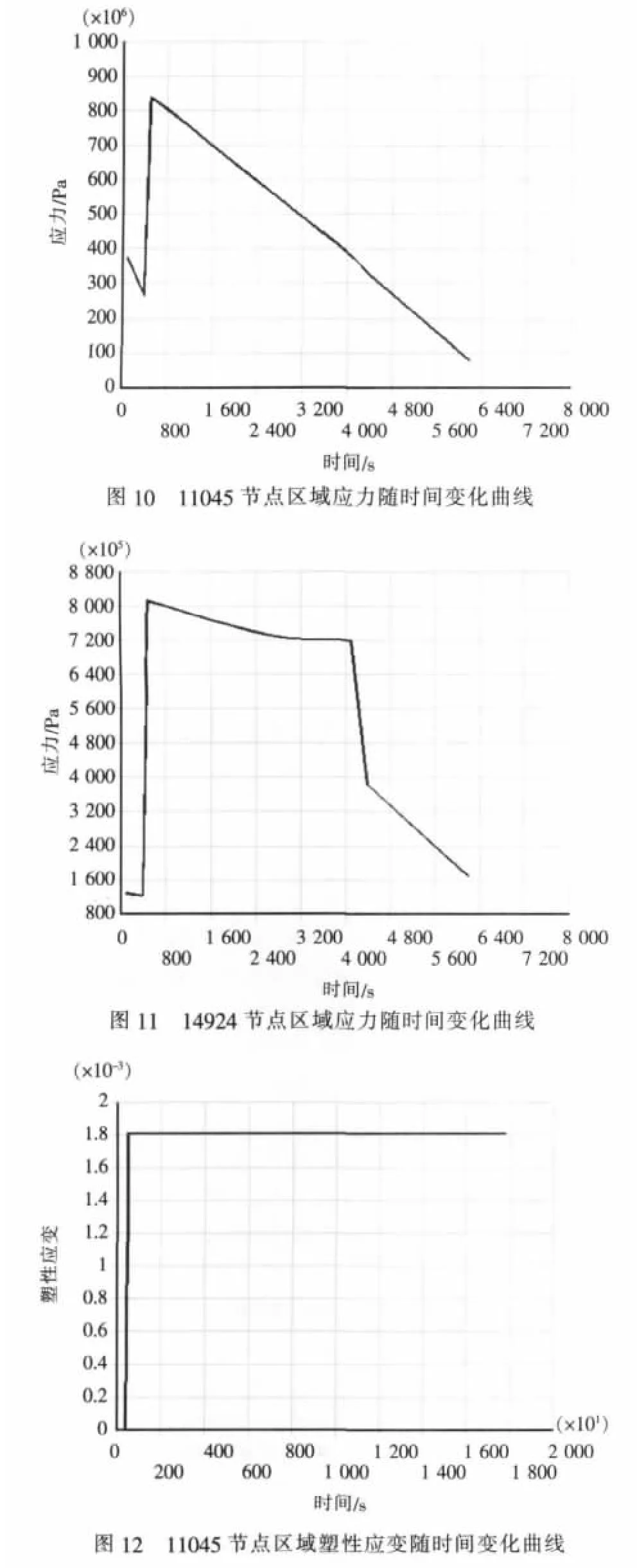
由图9可以看出涡轮叶片上存在两个危险区域11045号节点区域和14924号节点区域。图10和图11分别是11045号节点区域和14924号节点区域的应力随时间变化曲线。比较两节点处应力曲线的变化过程可以看出：11045号节点区域所受应力主要是温度变化引起的热应力，最大值达到820 MPa，该处复杂的结构以及直接与燃气接触是导致其高热应力的原因，而该处所受离心力引起的机械应力很小几乎可以忽略不计；14924号节点区域为离心力最大的区域，该处的应力为热应力与机械应力综合作用，两者之和在490 s时达到最大，随后热应力逐渐减小，在3200秒时热应力消失，此时的应力全部为机械应力，大小为720 MPa。图12和图13所示分别为三个循环下11045号节点区域和14924号节点区域的塑性应变随时间变化曲线。比较可以看出：11045号节点区域的塑性应变不随循环变化，即在燃气轮机卸载时此处无反向热应力；而14924号节点区域的塑性应变是循环变化的。因此可以认为11045号节点区域的疲劳失效属于应力疲劳，14924号节点区域的疲劳失效属于应变疲劳。另外涡轮叶片的蠕变应变只有1e－6量级，可以忽略不计。

4 涡轮叶片疲劳寿命研究

通常把零部件的疲劳寿命划分为疲劳裂纹起始寿命和疲劳裂纹扩展寿命，燃气轮机涡轮叶片的大部分寿命都消耗在疲劳裂纹起始上，叶片一旦出现宏观扩展裂纹，其疲劳裂纹扩展寿命相对于裂纹起始寿命来说较短，把这部分寿命计算到叶片的总疲劳寿命里，对涡轮叶片这样重要的零部件是不安全的，所以研究中一般都把裂纹起始寿命定义为涡轮叶片的疲劳寿命。

4.1 疲劳寿命预测公式

针对疲劳寿命的预测，国内外学者进行了很多的研究，提出了大量的疲劳寿命预测模型。目前较为通用的应力寿命预测模型为Basquin公式，由于Basquin公式没有考虑平均应力的影响，Kwofie［5］从疲劳强度系数的函数关系式出发，对Basquin公式进行了相应的修正，得到如下关系式：

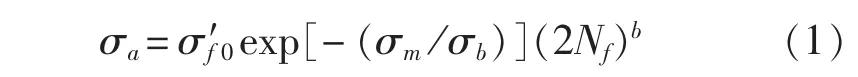
Manson－Coffin公式是目前应用最为广泛的应变疲劳寿命预测公式，其基本关系式如下：

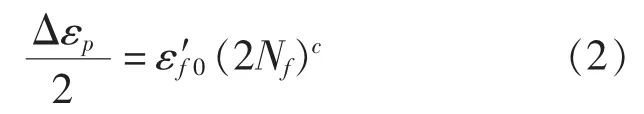
上式对短寿命区的寿命预测是适用的，对于长寿命区，塑性应变范围较小，考虑弹性应变范围以及平均应力对疲劳寿命的影响，将上式改写为：

4.2 涡轮叶片材料的疲劳特性参数试验测试

拟合材料疲劳试验结果，并得出疲劳寿命公式，是进一步分析涡轮叶片裂纹形成寿命的主要依据［6］。为了得出涡轮材料的应变－寿命曲线，本文参照GB6399－86进行了控制应变试验。

由图14可得涡轮叶片材料在平均工作温度下的 4 个基本参数为：σ′f0＝2 598 MPa，b＝－0.151，ε′f0＝ 0.108，c＝ － 0.712，σb＝ 1 008 MPa。 于是涡轮叶片材料的应变—寿命公式为：

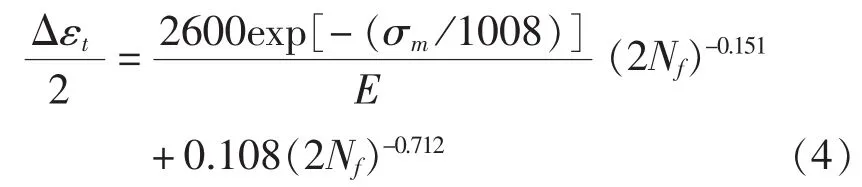
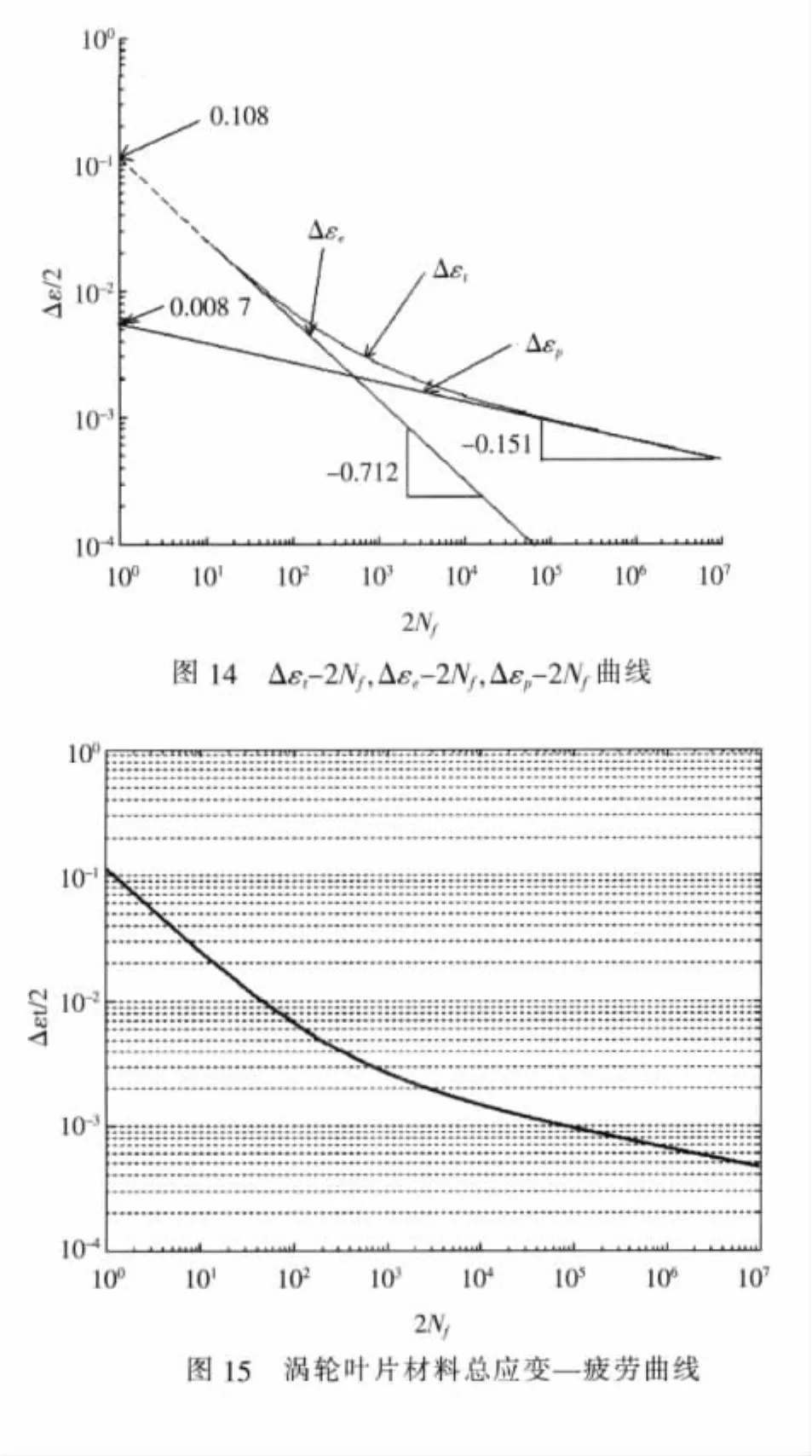
根据式（4）生成的应变—疲劳曲线如图15所示。

4.3 涡轮叶片寿命预测

由前文燃气涡轮叶片应力应变分析结果可知：11045号节点区域的失效模式为应力疲劳应采用Basquin公式计算其裂纹起始寿命，其最大应力为820 MPa，平均应力为410 MPa，代入式（1）计算得到11045区域相应的疲劳寿命为2965个循环。14924号节点区域的失效模式为应变疲劳应采用Manson－Coffin公式，其弹性应变范围为Δεe＝ 4.14 ×10－3，塑性应变范围为 Δεp＝ 0.3 × 10－3，平均应力为400 MPa，代入式（4）计算得到14924区域相应的疲劳寿命为2287个循环。

5 结 论

本文有以下5点结论：

1）燃气涡轮叶片受离心力、热应力和气流力的共同作用，采用单向热流固耦合法可以精确地计算燃气涡轮叶片的应力应变随时间的变化规律。

2）燃气涡轮叶片上有两处危险点分别是11045号节点区域和14924号节点区域。

3）11045号节点区域的失效模式是应力疲劳失效，14924号节点区域的失效模式为应变疲劳失效。

4）涡轮叶片疲劳特性试验为叶片寿命分析提供了必要的材料参数。

5）11045号节点区域的疲劳裂纹起始寿命为2965个循环，14924号节点区域的疲劳裂纹起始寿命为2287个循环。

［1］魏鹏飞，吴建军，陈启智.液体火箭发动机涡轮叶片结构特性的有限元分析［J］.国防科技大学学报，2005，27（2）：29－31.

［2］陶春虎，钟培道，王仁智.航空发动机转动部件的失效与预防［M］.北京：国防工业出版社，2001.

［3］REDDY TSR，et al.A review of recent aeroelstic analysis methods for propulsion at NASA Lewis research centre［R］.NASA Technical Paper 3406，1993.

［4］PERSSON C，PERSSON P O.Evaluation of service－induced damage and restoration of cast turbine blades［J］.Journal of Materials Engineering and Performance 1993，2（4）：5－9.

［5］KWOFIE S.An exponential stress function for predicting fatigue strength and life due to mean stresses ［J］.International Journal of Fatigue，2001，23：829－836.

［6］徐灏.疲劳强度［M］.北京：高等教育出版社，1988.

Analysis and Life Cycle Prediction of Marine Gas Turbine Blades Based on Thermal-Fluid-Structure Interaction

Zhu Jiang－jiang Yang Zi－chun
College of Naval Architecture and Power， Naval University of engineering， Wuhan 430033， China

Investigating the damage reduction control and the life cycle prediction of blade for purpose of improving the reliability，usability and maintainability of marine gas turbine need to analyze the structure performance of key components.Finite Element Method was used to carry out the three－dimensional analysis of thermal－fluid－structure interaction with regard to different stress and strain under emergent loading conditions.Experiment was performed to control the material strain of turbine blade， which would make inputs available for life cycle prediction，followed by stress and strain computation in typical loading spectrum.The results were used for computing the life cycle of fatigue cracks at two hazardous points by Basquin Equation and Manson－Coffin Equation.Analysis results can be utilized to predict the blades＇life cycle and thus provide reference for the operation and maintenance of gas turbine.

gas turbine blade； thermal－fluid－structure interaction； strain test； fatigue life； crack

TP202＋.1

A

1673－3185（2010）05－64－05

10.3969/j.issn.1673-3185.2010.05.013

2009－10-15

××装备预研基金项目（9140A27050106JB11）

朱江江（1982－），男，博士研究生。研究方向：热力系统的可靠性与故障诊断。E-mail：hanjiangxue12＠163.com

杨自春（1968－），男，教授，博士生导师。研究方向：热力系统的可靠性与故障诊断