数值模拟现代水面舰船带自由面的湍流绕流场

熊耀宇 段 宏 姜治芳 陈 立

中国舰船研究设计中心，湖北武汉 430064

数值模拟现代水面舰船带自由面的湍流绕流场

熊耀宇 段 宏 姜治芳 陈 立

中国舰船研究设计中心，湖北武汉 430064

为了研究带自由面的船舶湍流绕流场，选择了一艘ITTC推荐的公开船模作为模拟对象，数值求解RANS方程。此模型为带声呐导流罩和方形尾封板的复杂水面舰船。采用Ogrid块拓扑算法生成质量较高的纯六面体多块结构化网格，计算中采用RNG k－ε湍流模式和标准壁面函数，并使用VOF算法来捕捉自由面。空间离散采用QUICK格式，压力－速度解耦采用PISO算法。将阻力和波形的数值结果与实验数据相比较，总阻力系数误差约2%，船侧波形、船首自由面吻合良好，显示了CFD方法在船舶水动力学中预测带自由面湍流绕流场的有效性。

船舶阻力；自由面；波形；CFD；Ogird；湍流；水面舰船

1 引言

由于存在着不断增加的设计目标，现代水面舰船在设计过程中遇到了越来越多的困难［1］，比如舰首型线不仅要考虑减小阻力，还需降低噪声，而且要有用于声呐设备安装的空间构型。

当前，在船舶水动力学中，CFD已经成为了不可或缺的工具，不仅作为学术研究的手段，还可用做常规的设计工具［2］。其重要性不断增加，而带自由面的船舶湍流绕流场的数值模拟是其中的一个重要领域。

在船舶水动力学的数值计算中，CFD主要以如下几种方式得到应用：忽略粘性的流场计算［3］，在船模［4］或者实船［5］尺度下的粘性流场模拟以及无粘／有粘混合的分区计算方法［6］。无粘假设至今还被经常使用，不过RANS、DES和LES正在船舶粘性流场计算中发挥越来越大的作用。

本文选择了公开的DTMB 5415舰船模型用于CFD方法验证，此模型是ITTC推荐的舰船类型中的唯一公共数值模拟平台［7］。模型带有方形尾封板和用作声呐导流罩的球首。三家研究机构的船模实验数据得到了ITTC的认可和采用，分别是 ：DTMB 5415，IIHR 5512 和 INSEAN 2340。DTMB 5415 是缩尺比为 1／24.8 的模型，INSEAN 2340的几何构型与其完全相同，而IIHR 5512的缩尺比为 1／46.6。ISEAN 2340 模型的示意见图 1，几何尺寸见表1。

表1 舰船模型的主尺度

INSEAN与IIHR合作出具了一份公开的官方技术报告［8］，本文选其实验数据用作CFD结果验证。

本文中生成的多块结构化纯六面体网格具有良好的正交性，用其求解瞬态RANS方程来模拟船模绕流场，并与实验数据进行比较，主要关注点为阻力、船侧波形和首部自由面。

2 理论模型

2.1 控制方程

普适的连续性方程和N－S方程的张量形式［9］如下：

在船舶水动力学中，为了简化上述方程，采用不可压缩流体近似，并假设流体物性参数均匀且不变（密度、粘性系数等）。再假定船舶绕流场满足各态遍历假设，使用雷诺分解。在笛卡尔坐标系下，式（1）、式（2）简化为：

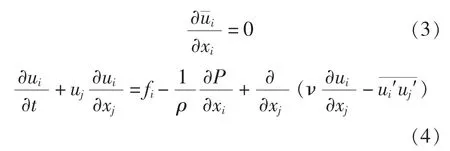
式中，ui，ui′分别为时均速度和脉动速度的i方向分量（i＝ 1，2，3）；为雷诺应力张量；下标满足爱因斯坦求和约定。

2.2 湍流模式

式（4）引入的雷诺应力张量有6个新的未知量，数值求解中必须加以封闭。最常用的封闭模式是Boussinesq的湍流涡粘假设［10］，忽略雷诺应力张量的历史效应，将其与速度导数张量的关系近似描述为：

方程中的经验常数取值见表2。

表2 RNG k－ε湍流模式的经验常数取值

方程中各项的详细物理意义和表达式参看文献［11-12］。

2.3VOF 方法

为解决流场计算中的自由边界问题，Hirt和Nichols提出了VOF方法［13］。船舶绕流场的自由面是典型的两相流态自由边界。当流体增多一相时，网格的每一个控制体积就会增加一个变量用于描述此相流体的体积分数。用αn表示第n相的体积分数，对于网格内的任意控制体积，可能存在以下3种情况：

αn＝0：控制体积内没有第n相的流体。

0＜αn＜1：控制体积内包含第n相流体与其他相流体的分界面。

αn＝1：控制体积内充满第n相的流体。

当流域中各网格内的相体积分数确定后，对位于两相交界面的控制体采用插值算法来确定自由面。

3 数值模拟

3.1 流域

建立笛卡尔坐标系如下：以基平面、中站面、中线面的交点作为原点O，X轴指向船尾为正，Y轴指向右舷为正，Z轴指向上方为正。

忽略尾流中可能存在的不对称涡街，假设船舶绕流场以中纵剖面为镜面对称。将中纵剖面作为流域的一个边界，以此减少流域体积和网格数量。

流域尺寸的设置参考文献［14］，并适当延长出流面和增高顶面以扩大计算流域。长方体流域的边界位置参看图2和表3。

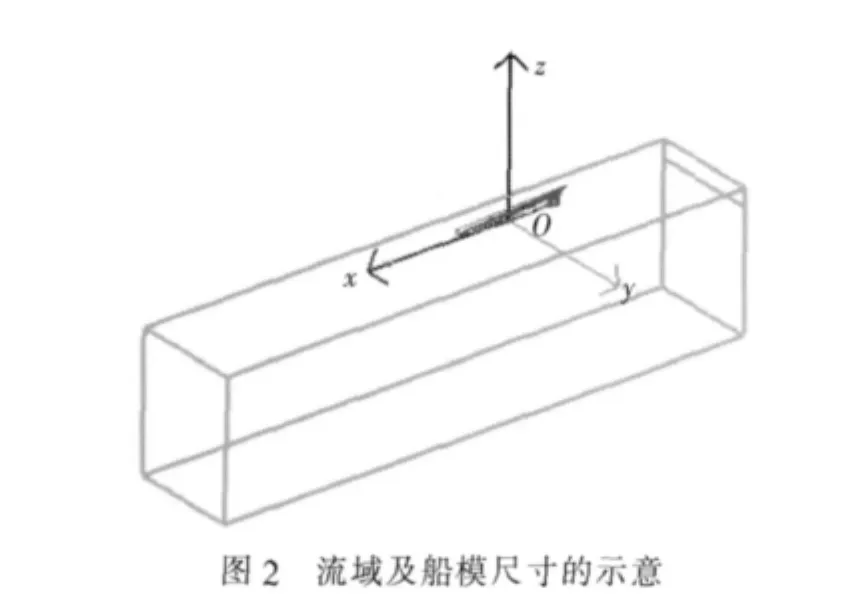
表3 流域边界的位置

3.2 网格

ITTC阻力委员会的最新报告中推荐使用纯六面体的结构化网络［2］，对上述流域使用专业网格软件ICEM CFD［12］生成多块结构化网格，得到的纯六面体网格包含了大约64.8万个有限控制体和67.8万个节点。

使用自上而下的剖分方法，将一个单块剖分为大约100个分块。在船表曲面形状复杂的地方使用Ogrid算法以提高网格质量，Ogrid拓扑分为内Ogrid和外Ogrid两种，其主要思想都是在一个块的四周创造数个环绕的块拓扑结构，详细的拓扑理论参看文献［15］。

在船表面所有地方，沿法线创造外Ogrid块作为边界层网格。对于首部导流罩区域，由于曲率过大，需要反复尝试调整节点位置和外Ogrid的形状以获得较好的网格质量，见图3。

在尾封板区域和上甲板前部区域，使用内Ogrid算法处理曲率过大的曲线，网格见图4和图5。

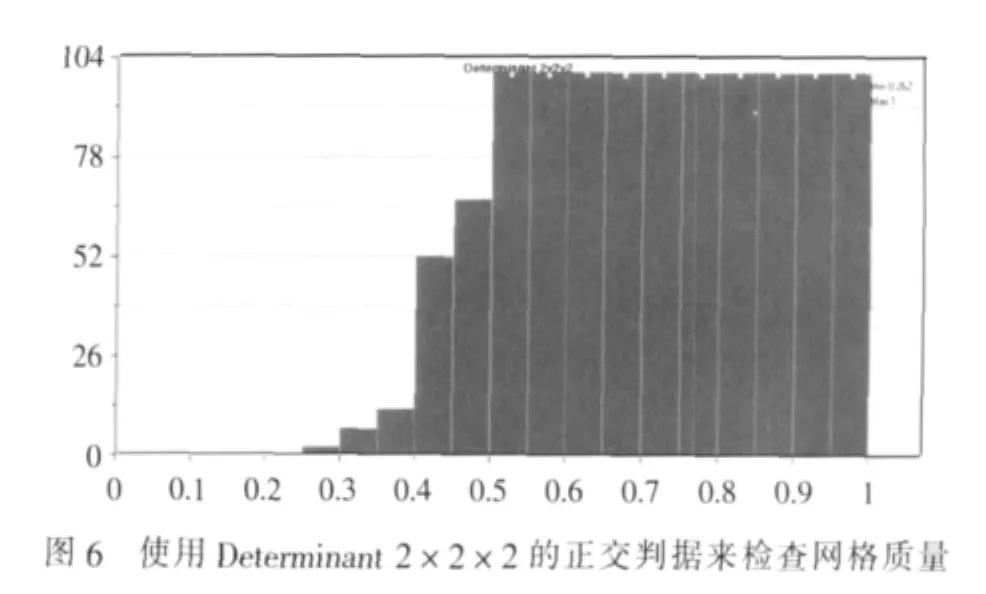
使用正交性算法 Determinant 2×2 ×2［14］检查网格质量，以此作为网格调整优劣的参考。参看图6，全部网格控制体的正交因子中，最小为0.262，大于 0.2，适合求解器使用［15］。 正交因子小于 0.5的网格控制体总数大约为100个，约占总数（64.8万）的 0.02%，其余 99.98%的网格控制体的正交因子大于0.5，显示了良好的网格质量。

由于在边界层内使用壁面函数法，边界层网格内首层节点需要布置在对数律层。本文先采用平板湍流边界层近似，求出首层网格节点的量级范围，约为mm级。在流场计算结束后，再检查船表面各处y＋的值，若不符合壁面函数法要求，就重新调整网格。边界层网格首层节点的法向高度取1.5 mm，并以1.1的等比因子递增15层。边界层网格的示意可以参看图3和图4，其合理性需要以流场的计算结果作为判据，参看下一节。

3.3 数值格式

使用PISO算法来处理压力—速度解耦；使用基于节点的格林高斯方法来处理梯度项；使用QUICK格式进行空间离散；使用二阶隐式格式进行时间离散。详细的数学机理参看文献［11，16］。

3.4 边界条件

在入流面，使用速度入口边界条件给定来流速度和湍流参数，布置两相流体积分数的分布。在出流面，使用压力出口边界条件编写UDF来描述静压贯穿两相并随高度变化的性质。在顶部面、底部面和右侧面，使用运动壁面边界条件给定其平移速度为来流速度。在中纵面，给定对称边界条件假定所有的物理量在此面为零通量。

3.5 初始条件

按照来流速度初始化整个流域，以水线面为界限给定两相流体积分数的分布并分区赋值湍流参数。

由于对时间项采用隐式算法，时间步长的给定并没有严格的判据。本文以柯朗数等于1为参照并经过多次试算，给出合适的时间步长。在迭代计算的初始阶段，Δt＝ 0.005 s， 待流场稳定后，再适当增加时间步长以节约计算的硬件资源。

4 计算结果及分析

4.1 计算的实验工况

选取的用于CFD验证的实验工况［8］见表3，此工况下，INSEAN重复做过10次测试，实验值为10次重复所取的平均值。

表3 选取的实验工况

4.2 阻力系数的数值结果

使用 Fluent软件［16］，数值求解非稳态 RANS方程，在数值时间约600 s后，总阻力系数平稳收敛，适当增加时间步长，继续计算至1 100 s。采用八核并行计算，单核主频2.6 GHz，耗费的计算资源约为500 CPU hours。得到的总阻力系数收敛曲线见图7。

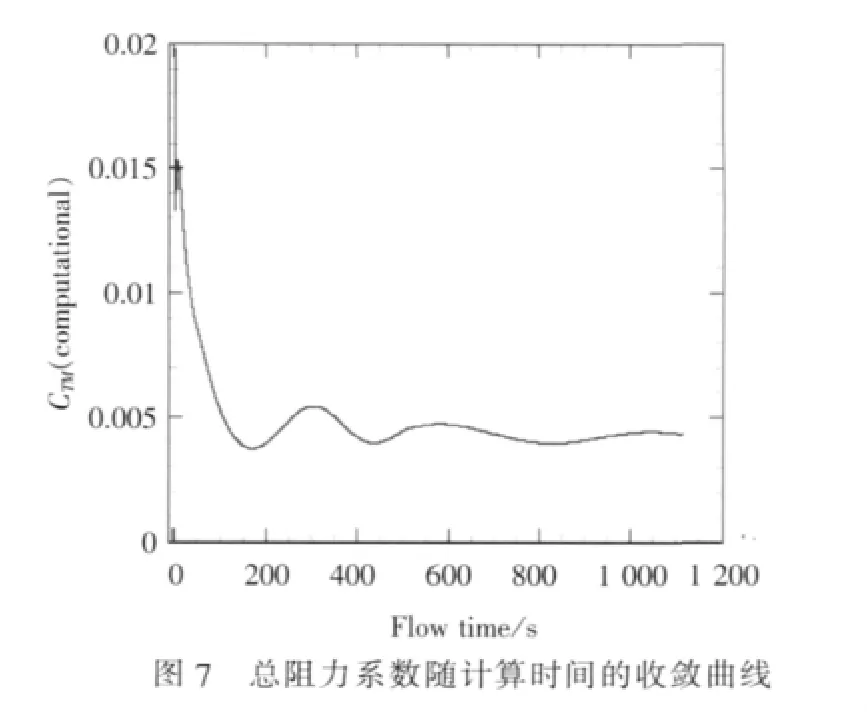
求解瞬态RANSE时，由于自由面的存在，总阻力系数呈现周期性的振荡，并逐渐收敛到稳定值。

计算得到的阻力系数与实验数据比较见表4。

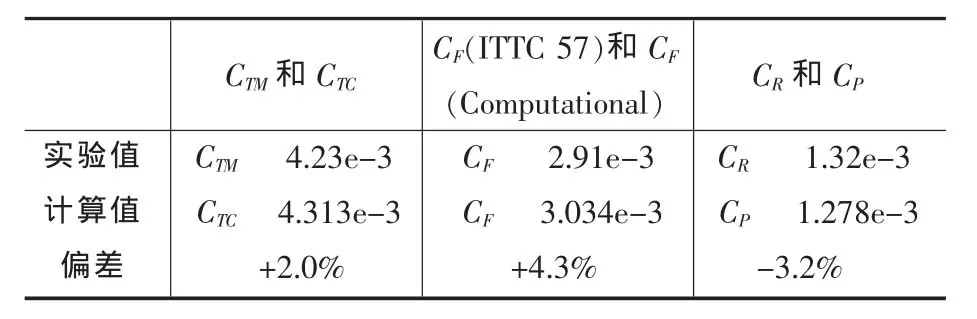
表4 阻力系数的数值模拟结果与实验值的比较

计算得到的总阻力系数与实验值的偏差约为2.0%，具有很高的精度，显示了CFD方法的有效性和应用前景。计算得到的摩擦阻力系数与ITTC 57公式的偏差约为4.3%，在工程的合理范围内。计算得到的压差阻力系数与实验的剩余阻力系数偏差约为－3.2%。

4.3 波形

自由面采用体积分数等值面作为分界面判据，取水的体积分数为50%，比较船侧波形曲线和首部波形自由面。

船侧波形曲线的计算值与实验值的对比如图8所示。首部自由面波形的计算、实验照片分别如图9、图10所示。

在船侧，波形曲线的计算值与实验值符合较好。首部的兴波形态能准确地模拟，首部横波波峰值偏差5%，其波形趋势良好。尾部横波的前半段（波高上升区域）能在曲线上定性地展现。船模表面其余各处的波形与实验值近似相同，数值结果清晰地捕捉到了两个波谷，与实验数据吻合。

4.4 y＋云图

壁面函数法忽略粘性底层的求解，通过工程公式来联系固壁处和边界层核心区的物理参量，因此壁面法线的第一个网格节点的高度有尺寸要求。

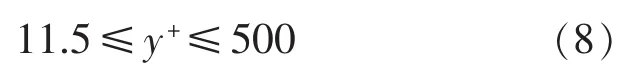
详细理论参看文献［10，16］。

利用云图检查船表曲面各处的y＋，其取值如图11所示。

在自由面以下的水相区域，30≤y＋≤179，参看公式（8），y＋分布满足壁面函数法的要求。

对于空气相，有部分网格 y＋≤11.5。高速行驶的船舶，其总阻力中的空气阻力比例很小，可忽略空气相网格的偏差所其带来的总阻力计算误差。

y＋云图表明了本文边界层网格的合理性。

5 结 论

为了对现代水面舰船的绕流场进行数值模拟和分析，本文选取了具有复杂曲面的ITTC DTMB 5415模型，利用RANS方程，求解高雷诺数下带自由面的湍流绕流场，计算结果与实验数据符合良好，显示了CFD方法在水动力学研究和船型设计领域的准确性和实用性，得到的结论如下：

1）数值模拟的结果与实验数据吻合良好，表明CFD可以为舰船设计人员提供可靠的设计参考，降低模型实验的成本，以加快新型舰船的研发进程。

2）求解RANS方程所得到的总阻力系数可以精确到2%，也能较准确地得到摩擦阻力（4.3%）分量和压差阻力（－3.2%）分量，表明 RANS方法在阻力计算方面的有效性。

3）采用VOF算法，计算得到的波形和自由面与实验吻合良好，表明此方法能比较精确地构造出自由界面的位置和形状。

4）多块结构化网格的质量需要通过反复调整节点位置来得到优化，Ogrid块拓扑算法具有强大的优势，能得到正交性很高的网格。

［1］CAMPANA E F， PERI D， TAHARAK Y，et al.Shape optimization in ship hydrodynamics using computational fluid dynamics［J］.Computer methods in applied mechanics and engineering，2006，196：634－651.

［2］International Towing Tank Conference ［R］.Proceedings of 25th ITTC.Fukuoka，2008.

［3］NOBLESSE F， YANG C.Alternative representations of steady potential flow about a ship ［C］//Proceeding of the 7th International Conference on Hydrodynamics （ICHD）.Italy，2006.

［4］WILSON W，FU T C，FULLERTON A，et al.The measured and predicted wave field of model 5365：an evaluation of current CFD capability［C］//Proceeding of 26th Symposium on Naval Hydrodynamics.Italy，2006.

［5］BHUSHAN S，XING T，CARRICA P，et al.Model and full－scale URANS ／DES simulations for athena R ／V resistance， powering and motions［C］//Proceeding of 9th International Conference on Numerical Ship Hydrodyanmics.Ann Arbor， MI， USA，2007.

［6］HUAN J C， HUANG T T.Surface ship total resistance prediction based on a nonlinear free surface potential flow solver and a Reynolds－Averaged Navier－Stokes viscous correction［J］.Journal of Ship Research，2007，51：47－64.

［7］International Towing Tank Conference.CFD，Resistance and flow benchmark database for CFD validation for resistance and propulsion［R］，1999.

［8］OLIVIERI A，PISTANI F，AVANZINI A，et al.Towing tank experiments of resistance， sinkage and trim， boundary layer，wake and free surface flow around a naval combatant INSEAN 2340 Model ［R］.IIHR Technical Report No.421，IIHR，2001.

［9］BATCHELOR G K.An introduction to fluid dynamics［M］.Cambridge： Cambridge University Press， 2000.

［10］STEPHEN B P.Turbulent flows ［M］.Cambridge：Cambridge University Press， 2000.

［11］VERSTEEG H K，MALALASEKERA W.An introduction to computationalfluid dynamics， the finite volume method［M］.Person Education Ltd，2007.

［12］ORSZAG S A， YAKHOT V， FLANNERY W S， et al.Renormalization group modeling and turbulence simulations［C］//International Conference on Near－Wall Turbulent Flows， Tempe， Arizona，1993.

［13］HIRT C W，NICHOLS B D.Volume of fluid （VOF）method for the dynamics of free boundaries［J］.Journal of computational Physics， 1981， 39： 201－225.

［14］ZHANG Z R，ZHAO F，LI B Q.Numerical calculation of viscous free－surface flow about ship hull ［J］.Journal of Ship Mechanics，2002（6）：10－17.

［15］ANSYS Inc.ANSYS ICEM CFD Manual［S］， 2009.

［16］ANSYS Inc.ANSYS FLUENT Guide［S］， 2009.

Numerical Simulation of Modern Surface Ship in Free Surface Turbulent Flow

Xiong Yao－yu Duan Hong Jiang Zhi－fang Chen Li
China Ship Development and Design Center， Wuhan 430064， China

A public ITTC recommended complex modern surface ship model with sonar dome and transom stern was chosen for numerical simulation of free surface turbulent flow.Pure hexahedral multiblock structured grids with fine quality were generated by using Ogrid topology.Transient RANSE were numerically calculated and the RNG k－ε turbulence model with standard wall functions was employed.The VOF algorithm was applied to track free surface.QUICK scheme was used for spatial discretization and PISO scheme for pressure－velocity coupling.Computational results including resistance coefficients and wave profile were compared to experimental data with good agreement.The total resistance coefficient has a bias of two percentage，wave profile and bow free surface accord the data with a good precision，showing that CFD method can effectively predict the free surface turbulent flow in ship hydrodynamics.

ship resistance；free surface；wave profile；turbulent flow；CFD；Ogrid；surface ship

U661.1

A

1673－3185（2010）06－16－05

10.3969/j.issn.1673-3185.2010.06.004

2010-02-19

熊耀宇（1985－），男，硕士研究生。研究方向：船舶水动力学。E-mail：xiong－yaoyu＠ hotmail.com

段 宏（1954－），男，研究员。研究方向：舰船总体研究设计