涡轮盘低循环疲劳两种可靠性分析方法的对比

刘 辉，白广忱

（北京航空航天大学 能源与动力工程学院，北京 100191）

涡轮盘是航空发动机主要承力构件之一，随着发动机推重比的增大，涡轮盘的设计应力水平逐渐提高，其使用寿命大大降低，而涡轮盘的低循环疲劳断裂，往往会导致十分严重的后果。因此研究涡轮盘的低循环疲劳可靠性，对飞行安全具有重要意义。

疲劳寿命分析，有基于应力的和基于应变的两种方法。基于应力的方法，最早被应用于疲劳分析，其以分析应力与寿命的关系为主，具有简单易行的特点，能满足一般结构设计分析要求。而基于应变的方法，在分析塑性应变起主要作用的低循环疲劳时具有优势。严格意义上的低循环疲劳故障，其疲劳断裂周次小于疲劳过渡寿命，对于大多数用作压气机和涡轮盘的钛合金和高温合金，其疲劳过渡寿命仅为102～103循环之间。而航空发动机涡轮盘寿命，一般在103～105之间，因此，涡轮盘结构并不存在本质意义上的塑性应变损伤占主导的低循环疲劳[1]。本文分别利用基于应力和基于应变的疲劳可靠性分析方法，来计算航空发动机涡轮盘低循环疲劳寿命及可靠度，对两种方法的计算结果进行了比较和分析。

1 疲劳寿命可靠性的两种模型

涡轮盘疲劳可靠性问题，一般面临解决两类问题：一是具有一定可靠度的轮盘寿命是多少，二是一定轮盘寿命所具有的可靠度是多少。第一类问题，可用载荷寿命模型求解；而第二类问题，可用载荷强度模型求解[2]。

1.1 应力疲劳可靠性模型

应力与寿命的关系，一般由S-N曲线描述，不同存活率的S-N曲线构成P-S-N曲线。目前在疲劳可靠性设计中，常用的经验公式有三种，其中如式(1)所示的三参数幂函数，具有较大的优越性[3]。函数中的A、B、C均为常数，可由回归分析得到，而传统的同方差回归分析，无法考虑到不同温度和应力时其寿命分散性的差别，因此本文用异方差回归分析的方法，回归出所需的三参数幂函数。

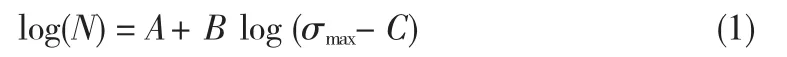
由于疲劳实验数据是在确定的应力比下得到的，但在实际的工程应用中，危险位置的应力比往往是变化的，所以要对得到的应力与寿命的关系进行修正，一般采用Goodman曲线，由式 σa/σ-1+σm/σb=1描述。

（1）应力寿命模型。应力寿命模型的可靠度表示为

Nσ为轮盘寿命，Nσ0为设计寿命。

轮盘寿命可由描述P-S-N曲线的三参数幂函数得到，函数中的应力项，可通过有限元计算得出。为了便于抽样计算，首先可拟合出涡轮盘危险点的最大应力的响应面方程。根据数据手册上的实验数据[4]，进行异方差回归，260℃时GH4133材料在置信度为0.5和0.95下的三参数幂函数分别表述为式(3)和式(4)：

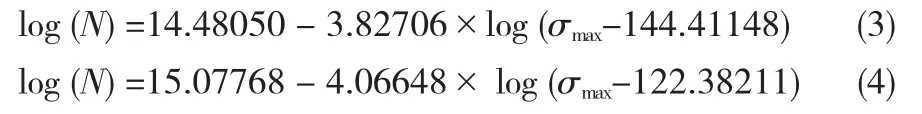
计算出的应力经过Goodman曲线修正后，代入式(3)和式(4)，就可得到疲劳寿命。

（2）应力强度模型。应力强度模型的可靠度表示为

σN为应力强度，σt为应力载荷。

不同可靠度、不同置信度的应力强度，可由拟合的P-S-N曲线得到。给定寿命N后，可代入式(3)和式(4)，分别计算出置信度0.5和0.95下的应力强度，而应力载荷可由有限元计算得出，本文由涡轮盘危险点的最大应力的响应面方程得到。

1.2 应变疲劳可靠性模型

应变与寿命的关系由ε-N曲线描述，而基于存活率P的P-ε-N曲线能够较好的描述材料在给定应变水平下的疲劳寿命的概率分布特性。用Mason-Coffin公式来拟合P-ε-N曲线在低循环疲劳寿命分析中应用较广泛。异方差回归的分析方法同样可以应用在拟合P-ε-N曲线的过程中。

（1）应变寿命模型。应变寿命模型是以疲劳寿命为参数的可靠性模型，可靠度表示为

轮盘寿命可由经过平均应力修正的Mason-Coffin公式得到。对于GH4133材料，置信度水平0.5和0.95下，用Morrow修正项修正过的Mason-Coffin公式分别为式(7)和式(8)[2]。

式中的循环应变幅由有限元计算得出，同样为了便于抽样计算，可先拟合出涡轮盘危险点的最大应变的响应面方程。将计算得到的循环应变幅分别代入式(7)和式(8)，就可得到置信度0.5和0.95下的疲劳寿命。

（2）应变强度模型。应变强度模型的可靠度表示为

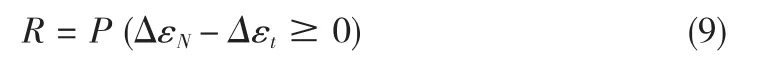
△εN为应变强度，△εt为应变载荷。

应变强度由P-ε-N曲线给出，在给定寿命N下，可将寿命N代入用Morrow修正项修正过的Mason-Coffin公式分别计算出置信度0.5和0.95下的应变强度。应变载荷可用有限元法计算，本文由响应面方程得到。

2 涡轮盘的应力应变计算

用于计算的涡轮盘的外形和有限元模型如图1所示，为某发动机高压一级涡轮盘，经过适当的简化，将其视为轴对称模型，利用ANSYS进行温度场及弹塑性分析，得知涡轮盘中心孔边缘上一点应力最大，将此点定为危险点。涡轮盘所用材料为GH4133，最大工作转速11 440 r/min。

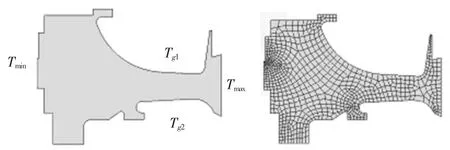
图1 涡轮盘外形和有限元模型

将计算过程中的涡轮盘前后侧冷却空气温度Tg2和Tg1、轮缘轮心温度和Tmax、Tmin涡轮盘转速ω和对应转速均值时的轮缘均布载荷σw选为随机变量，所选随机变量均为正态分布，其均值和标准差如表1所示。

表1 随机变量分布表

用中心复合因子法得到13组样本点，用这13组参数重新进行有限元计算，分别拟合危险点的最大应力和应变变程二次响应面方程，即式(10)和式(11)。

3 涡轮盘寿命分布及可靠度计算

对应力寿命模型，由Monte-Carlo法对6个随机变量抽样1万次，并代入模型计算得到了置信度为0.5和0.95下涡轮盘的疲劳寿命的分布（如图2所示）。可以看出，疲劳寿命并不服从正态分布，而是明显呈偏态分布。

图2 置信度为0.5（左）和0.95（右）涡轮盘疲劳寿命分布

对应力强度模型，由Monte-Carlo法对6个随机变量抽样1万次，并代入模型计算得到的可靠度随循环数变化的结果如图3所示，高置信度下的可靠度曲线，在低置信度下曲线的左侧，且在循环数为2 000至6 000段内，可靠度相差较大，最大处相差近50%。

图3 置信度为0.5和0.95的涡轮盘可靠度

对应变寿命模型，经过抽样计算得到的置信度为0.5和0.95下的疲劳寿命的分布如图4所示，疲劳寿命同样不服从正态分布，而是呈明显的偏态分布。

对应变强度模型，经过抽样计算得到的可靠度随循环数变化的结果如图5所示，两种置信度下可靠度曲线的位置与变化趋势，均与应力强度模型相同；不同的是，应变强度模型在整个寿命区间上两种置信度下，可靠度相差并不大，最大处仅为16.9%。这说明，与应力强度模型相比，应变强度模型对置信度不敏感。

将置信度为0.5时，不同模型对应不同可靠度水平的轮盘概率寿命列表比较，如表2所示。

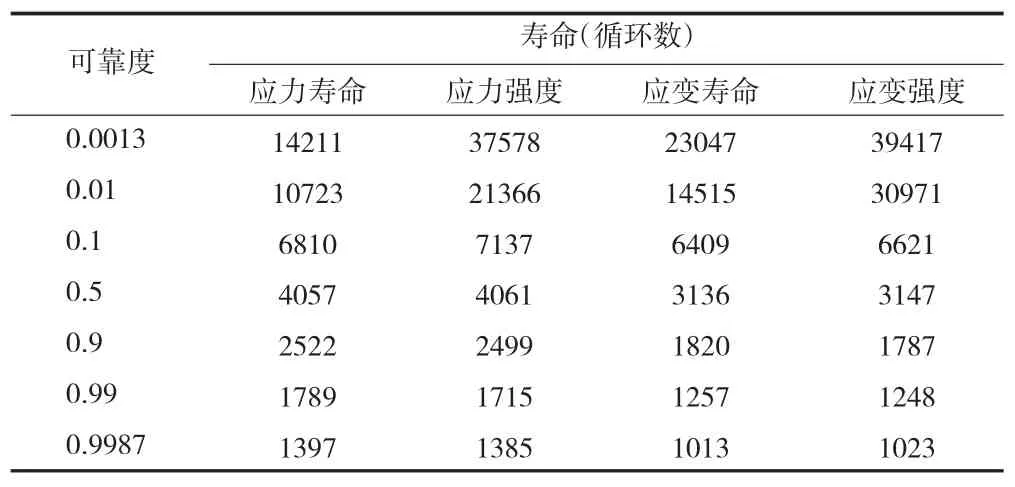
表2 置信度为0.5时根据4种模型得到的涡轮盘寿命

可以看出，对应力寿命模型和应变寿命模型，可靠度为0.0013时，相对误差为38.3%；可靠度为0.5时，相对误差为29.4%；可靠度为0.9987时，相对误差37.9%。对应力强度模型和应变强度模型，可靠度为0.0013时，相对误差4.7%；可靠度为0.5时，相对误差为29.0%；可靠度为0.9987时，相对误差为35.4%。

可以看出，与两种寿命模型不同，低可靠度时，两种强度模型得到的涡轮盘寿命相差不大，而随着可靠度的提高，两种强度模型得到的涡轮盘寿命之差逐渐增大。总体上无论是两种寿命模型还是两种强度模型，都呈现出低可靠度时，基于应力模型的涡轮盘寿命较安全；而高可靠度时，基于应变模型的涡轮盘寿命较安全。同样的，无论是基于应力的模型，还是基于应变的模型，也都呈现出低可靠度时，根据寿命模型得到的的涡轮盘寿命较安全；而高可靠度时，根据强度模型得到的涡轮盘寿命较安全。但是可靠度大于0.5时，同样基于应力或基于应变的寿命模型和强度模型得到的涡轮盘寿命，均相差不超过5%，这说明，预估中高可靠度的涡轮盘寿命时，采用寿命模型或强度模型，得到的是相似的结果。

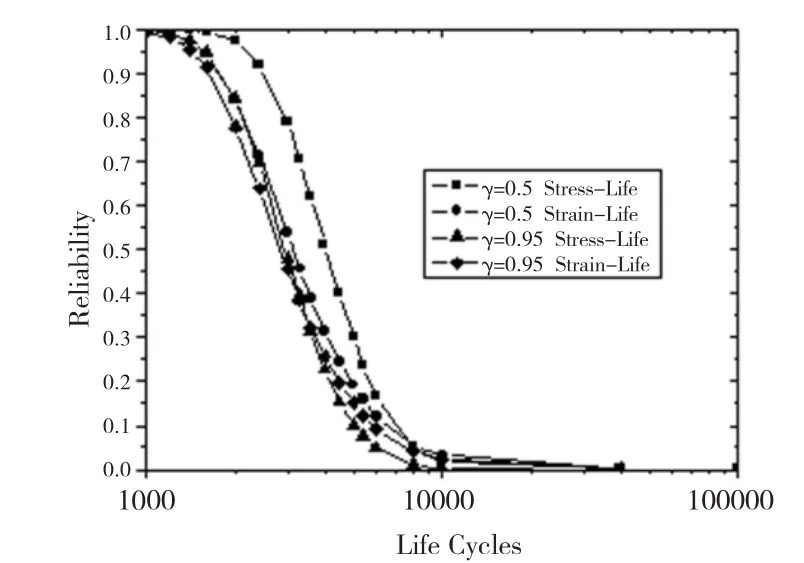
图6 置信度为0.5和0.95应力寿命与应变寿命模型计算得到的涡轮盘可靠度

置信度分别为0.5和0.95时，使用应力寿命与应变寿命模型计算得到的涡轮盘低循环疲劳可靠度随循环数的变化如图6所示。以应变寿命模型的计算结果为基准，置信度为0.5和0.95时，两种模型得到的可靠度差值如图7所示。

图7 置信度为0.5(左)和0.95(右)应力寿命与应变寿命模型计算得到的涡轮盘可靠度之差

图8 置信度为0.5和0.95应力强度与应变强度模型计算得到的可靠度

置信度分别为0.5和0.95时，使用应力强度与应变强度模型计算得到的涡轮盘低循环疲劳可靠度随循环数的变化，如图8所示。以应变强度模型的计算结果为基准，置信度为0.5和0.95时，两种模型得到的可靠度差值如图9所示。

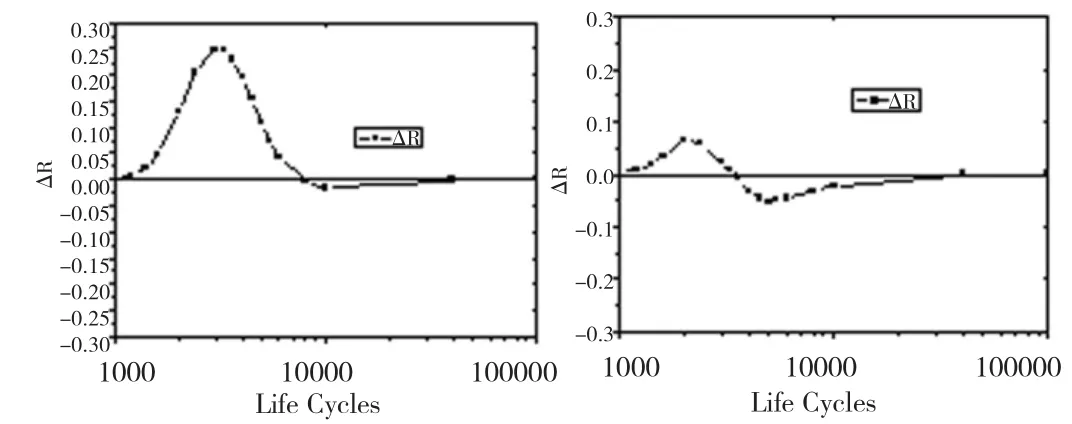
图9 置信度为0.5(左)和0.95(右)应力强度与应变强度模型计算得到的可靠度之差

由图6和图7可以看出，置信度为0.5时，应力寿命模型与应变寿命模型得到的涡轮盘低循环疲劳可靠度差别较大，尤其是在循环数2 000至5 000区间上，应力寿命模型的可靠度，明显高于应变寿命模型的可靠度，且相差均超过0.1，最大绝对误差为0.251 2，相对误差为46.4%。置信度为0.95时，应力寿命模型与应变寿命模型得到的涡轮盘低循环疲劳可靠度差别较小，在整个低循环区间上，绝对误差均小于0.1，绝对误差最大达到0.065 2，此时的相对误差只有8.36%。考虑到P-S-N及P-ε-N曲线在低循环区间上的拟合误差、涡轮盘危险点处最大应力和循环应变幅的响应面方程的拟合误差及数值计算过程中产生的计算误差，高置信度时，计算结果的相似，可以说明应力寿命模型和应变寿命模型均可用于计算涡轮盘低循环疲劳可靠度。

图8与图6相似，而图9与图7相似，这也能说明采用寿命模型和强度模型能得到相似的结果。而由图8和图9的可以看出，高置信度下应力强度模型与应变强度模型得到的可靠度，在整个低循环区间上仍然相差较小，考虑到基于应变的涡轮盘低循环疲劳可靠性分析不仅需要应力分析、材料的P-ε-N曲线数据，还需要材料的循环应力应变关系曲线数据，相对来说，基于应力的分析方法成本较小，所以可以采用基于应力的疲劳可靠性分析方法，来分析涡轮盘低循环疲劳可靠性。

4 结束语

本文对比了基于应力和基于应变的疲劳可靠性分析方法在涡轮盘低循环疲劳分析中的应用。基于应力的分析方法，在高置信度下，和基于应变的分析方法具有相近的计算结果。基于应力的疲劳可靠性分析模型简单，理论成熟，避开了复杂的循环应力应变分析，为涡轮盘低循环疲劳寿命预测与可靠性分析提供了另一种思路。

[1]陶春虎，钟培道，王仁智，等.航空发动机转动部件的实效与预防[M].北京：国防工业出版社，2000.

[2]高 阳.航空发动机涡轮盘低循环疲劳可靠性分析[D].北京：北京航空航天大学，2009.

[3]高镇同，熊俊江.疲劳可靠性[M].北京：北京航空航天大学出版社，2000.

[4]北京航空材料研究所.航空发动机计算用材料数据手册[K].北京：国防工业出版社，1989.