装药量及水深对水下爆炸气泡动态特性的影响*
李 健,荣吉利,项大林
(1.北京理工大学宇航学院,北京100081;2.广西工学院汽车工程系,广西 柳州545006)
水下爆炸大体可分为3 个阶段:装药的爆轰、冲击波的产生和传播、气泡的形成和脉动。当爆轰过程结束后,冲击波以几倍于水中声速的速度传播并首先作用于水中结构,且作用时间短、压力峰值高,形成对结构的局部破坏,由于气泡脉动频率与舰船前几阶固有频率接近,极易造成船体总体结构的破损或舰载设备的破坏。根据J.R.Blake 等[1]、P.C.Chan 等[2]的研究,多数情况下,在气泡收缩阶段,由于Bjerknes 力作用,气泡会被水中结构吸引而向结构方向运动,在浮力、惯性力等因素的影响下,沿着气泡坍塌方向会形成高速射流,且射流会穿透气泡并冲击气泡壁的另一面,最终作用于水中结构并对结构形成再次破坏。随后气泡体积收缩至最小并开始第2 次脉动,但能量相对前1 次已经大为降低。因此,水下结构除了受到水中冲击波的作用外,还会受到气泡脉动压力、射流的作用。所以,针对水下爆炸气泡运动和射流特性的研究对弹药毁伤威力及目标易损性的评估都具有重要的意义。
J.R.Blake 等[3]、Q.X.Wang 等[4]、Y.L.Zhang 等[5]和C.Wang 等[6]对气泡的运动特性进行了研究;E.Klaseboer等[7-8]对气泡与水中结构相互作用进行了实验研究,并采用边界元法对气泡的运动特性进行了研究,验证了数值计算方法的正确性;A.Pearson 等[9]对单个及2 个气泡与自由水面相互作用进行了研究,计算结果与实验结果具有较好的一致性;Z.Zong[10]研究了水中细长梁与短粗梁在气泡脉动作用下的动力响应;N.Takada 等[11]采用Lattice Boltzmann 方法对刚性壁面附近的气泡进行了研究,取得了较理想的结果;Y.X.Zong[12]采用边界积分方法研究了气泡的运动特性,计算结果与实验值吻合较好。
边界元方法只在边界离散,大大降低了计算成本,但是在气泡射流产生及与结构相互作用方面有一定的局限性,目前研究成果较少;通常采用与有限元相结合的方法进行气泡特性的研究。为了对水下爆炸数值模拟研究提供有益的补充,本文中,将以体积加速度模型为基础,基于MSC.DYTRAN 非线性有限元软件,应用FORTRAN 语言开发定义流场初始条件和边界条件的子程序,研究水下爆炸气泡脉动全过程,并与现有实验数据进行对比,验证有限元模型、程序开发和计算的正确性与准确性,并讨论装药量、水深等因素对气泡射流速度的影响。
1 理论背景
1.1 气泡运动初始条件
模拟气泡的运动,需要先求出气泡的初始半径。采用气泡体积加速度模型来确定气泡初值,基本思路就是以流场中某一固定点的压力变化为研究对象,分别研究气泡体积加速度和炸药参数与固定点压力变化之间的关系,联立求解即可确定气泡体积加速度与炸药参数、时间之间的关系。P.A.Frost 等[13]提出了气泡体积加速度模型

式中:p 为压力,R 为传播距离,V 为气泡体积,ρ为流体密度。式(1)描述了气泡体积对时间2 次导数与流场压力的关系,K.S.Hunter[14]为了将体积加速度模型适合于超声速研究,对式(1)进行适当修正

式中:ac为药包半径,A、B 为常数。
由文献[14-16],流场中压力、药包半径、距离、时间等变量之间的关系为
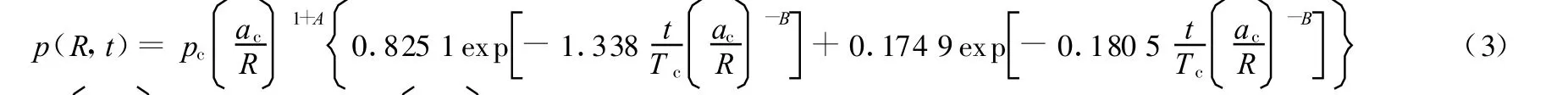

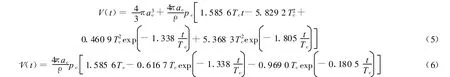
计算结果与文献[14]中的表达式略有不同。
图1 为55 g 球形炸药在3.5 m 水深工况下、t/T c 在0~10 时、气泡半径和径向速度的时程曲线。炸药起爆后,首先是爆轰过程,压力瞬间增加,药包径向加速度非常大,因此故径向速度变化率非常明显,爆轰结束后,膨胀速度逐渐平缓,随后产物形成的气泡将以小于声速向外膨胀。针对这一规律,从图中观察,气泡径向速度变化率由急速到平缓,因此可以认为当t >0.1 ms 时爆轰结束,爆轰产物所形成的气泡将以小于声速向外膨胀,可将此刻气泡半径值作为气泡脉动的初值进行计算。
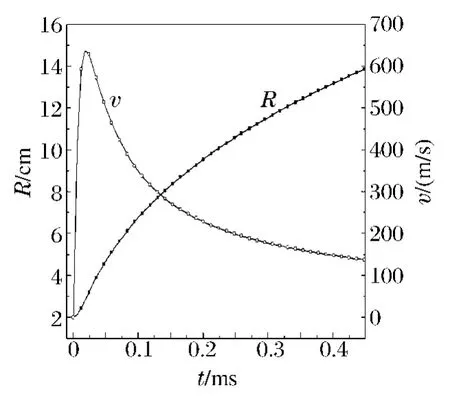
图1 气泡半径及径向速度时间历程曲线Fig.1 Time-history curves for radius and velocity of bubble
1.2 状态方程
忽略气泡运动对气体压力的影响,认为气泡内的压力仅和气泡的初始状态及其体积有关,即气泡内的压力p 与气泡体积V 的关系为

式中:pc为可冷凝气体的饱和蒸汽压,量级与大气压相当,一般可忽略;p0和V0分别为气泡形成时的初始压力和初始体积;γ为气体的比热比,对于TNT 水中爆炸的爆轰产物,γ取1.25。
1.3 经验公式
气泡最大半径的经验公式为

式中:Rm为气泡半径,m;W 为装药量,kg;p0为周围水的静压力,Pa;K 为常数。气泡脉动周期经验公式为

式中:T 为气泡的脉动周期,s;W 为气泡的装药量,kg;z0 为气泡所处位置的流体静压的等效水深,m。
根据上述经验公式,可以计算出气泡脉动过程中的最大半径以及脉动周期。
2 数值计算研究
为了验证数值计算的正确性,首先根据已有实验数据,对自由水域中气泡脉动进行数值计算。实验数据[7]简单描述如下:实验在一个直径约18 m、高7 m 的水池中进行。药量为55 g 球形炸药,爆心位置在水池中心水面以下3.5 m 处,并在水池中放入每秒1 000 帧的高速摄影仪拍摄气泡脉动演变的全物理过程,气泡演变过程实验结果如图2 所示。

图2 55 g 炸药水下3.5 m 处爆炸气泡实验结果Fig.2 Bubble shape evolution under the 55 g charge mass at the depth of 3.5 m f rom experiment
2.1 有限元模型
对于水下爆炸来说,冲击波是以指数形式衰减的,48%的能量在25 个药包半径的体积内散逸掉[17]。对于上述实验,由于爆心到自由界面、爆炸池底部及爆炸池壁面的距离均远大于25 倍药包半径,因此,计算将不考虑冲击波反射效应。计算模型是一个边长为1.5 m 的正方体。流场采用欧拉单元描述,炸药位于模型正中部。网格采用中间密、四周疏的分布方式,即爆心处网格最密。爆心处单元对角线长度为55 g 药包半径的约0.3 倍,10 g 药包半径的约0.53 倍,最大单元对角线长度为药包半径的约1.5 倍。
2.2 初始条件及边界条件定义
数值计算不但要确定气泡初值,还要确定流场的初始条件和边界条件。MSC.DYTRAN 并不能通过直接定义重力加速度实现流场静水压力的定义,而条件透射边界(即当边界两侧出现压力差时,流体会从高压区通过边界流向低压区)不能直接在单元表面进行定义。因此,将根据初值及边界条件特点,采用FORTRAN 语言,根据软件提供的定义初值和边条的子程序接口EXINIT 及EXFLOW2 定义流场的初值和边界条件。通过EXINIT 子程序求出每个流场单元所处水深的静水压力值,结合相应的变换将数值赋予每个流场单元。同理可以通过EXFLOW2 将流场对应的压力值赋到流场边界上。
2.3 与实验结果对比

图3 55 g 炸药水下3.5 m 处爆炸气泡计算结果Fig.3 Bubble shape evolution under the 55 g charge mass at the depth of 3.5 m f rom calculation
为了更好地对比数值计算与实验实测的气泡形状,尽可能与实验同步比较,计算结果如图3 所示。从图可以看到气泡在第1 次脉动周期内的全过程,且当气泡收缩到体积最小时,由于此刻浮力作用,气泡坍塌从底部开始,随即产生指向自由界面的射流。对比图2~3 可以看到,在t=96 ms 前,有限元计算结果与实验结果具有高度的一致性。观察实验结果,对于气泡后续的运动,由于周围的引线装置,对气泡的运动产生了一定的影响,且图像相对较模糊,因此与数值计算结果产生了一定的偏差。纵观气泡演变的全过程,计算结果与实验结果吻合相当好。
E.Klaseboer 等[7]不但分别对10、35 和55 g 球形装药在水下3.5 m 处进了实验研究,而且还采了边界积分方法对气泡运动进行了数值模拟。本文中采用了有限元方法对以上各工况进行数值模拟,并将计算结果与边界元、实验结果进行对比,如图4 所示。从图中可以看出,本文的计算结果比文献[7]中所采用的边界积分法的计算结果更接近于实验值。特别随着装药量的增加,计算值与实验结果具有高度的一致性,随着药量的减小,误差也相应有所增加,此现象与有限元网格密度有关。
表1 为3 种装药量下,分别采用实验测试、有限元和边界元3 种方法对气泡第1 次脉动周期内最大体积和误差。从表中可以看到,有限元计算结果在各种工况下较边界元计算结果要更接近于实验结果,且误差均能保持在10%以内。二者与实验结果的误差趋势基本一致,即随着装药量的减小,数值计算精度会有所降低。以上3 种工况采用了完全相同的有限元模型,因此,随着装药量的减小,有限元模型的网格密度相对降低了,从而数值计算结果的精度也有所降低。因此,若要提高数值计算精度,应当适当提高有限元网格密度。

表1 实验测量、有限元及边界元计算结果的比较Table 1 Comparison of bubble volume among the FEA,BEM and experiment
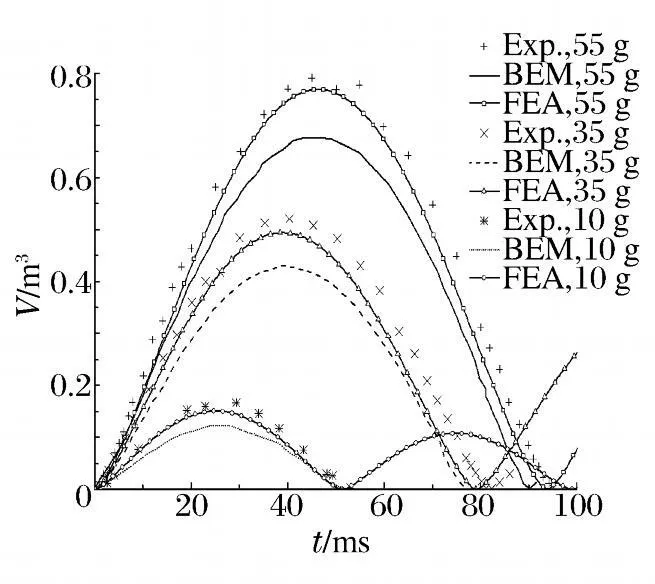
图4 计算结果与实验结果的对比Fig.4 Comparison of bubble volume between experiment and calculation
3 特征参数对气泡动态特性的影响
3.1 装药量对气泡动态特性的影响
为了研究装药量变化对气泡动态特性的影响,以爆心位于水下100 m 处、球形药包质量在50 ~500 kg 变化系列工况为研究对象,计算气泡的体积、脉动周期、最大半径以及射流速度。图5 为500 kg 炸药在水下100 m 处气泡脉动与射流形成过程。从图中可以看到,气泡在脉动过程中会逐渐向自由面移动,当气泡在第1 次收缩到体积最小时,坍塌从气泡底端开始,产生指向自由面的射流,射流速度增加较快,并在336 ms 时击穿气泡,此后,气泡将以环状形式膨胀。

图5 500 kg 炸药水下100 m 爆炸气泡脉动过程Fig.5 Evolutions of bubble for 500 kg detonation at the depth of 100 m from calculation
图6 为相同水深不同装药量情况下气泡体积的时间历程曲线。对比各工况下相应时刻的气泡体积可以看到,在爆心位置相同的情况下,气泡最大体积随着装药量的增加而增加;对于相同装药量,在对应的脉动周期内,气泡的体积会随着脉动的进行而减小。根据气泡体积变化曲线还可以提取气泡脉动的周期,并将数值计算结果与经验公式进行对比,结果如图7 所示。从图中可知,在爆心位置相同的情况下,气泡脉动周期会随着装药量的增加而增加。数值计算结果与经验公式的误差保持在6.9%~10.8%之间。
图8 为不同药量所对应的气泡最大半径。从图中可以看到,气泡最大半径随着装药量的增加而增加,与经验公式(9)对比后发现,数值计算结果与经验公式的误差较小。从气泡脉动周期以及最大半径与经验公式的对比中可以发现,数值计算结果与经验公式趋势一致,误差较小,证明了数值计算结果的正确性。
图9 为气泡形成直至被射流击穿变成环状气泡过程中,正下方壁面运动速度的时间历程曲线,以垂直向上为正。从图中可以看到,气泡具有负向初速度,但速度大小会随着时间的推移而逐渐减小,在经过一段较平缓的变化后,气泡壁的速度会迅速增加。气泡的运动周期增大,气泡的射流速度降低;药量减小,射流速度增大。也就是说,小药量的药包爆炸产生的射流可能对结构造成严重的局部毁伤,射流速度可达数百米每秒,而大装药量药包爆炸形成的射流速度低,但射流影响区域很宽,对舰船结构造成总体破坏。
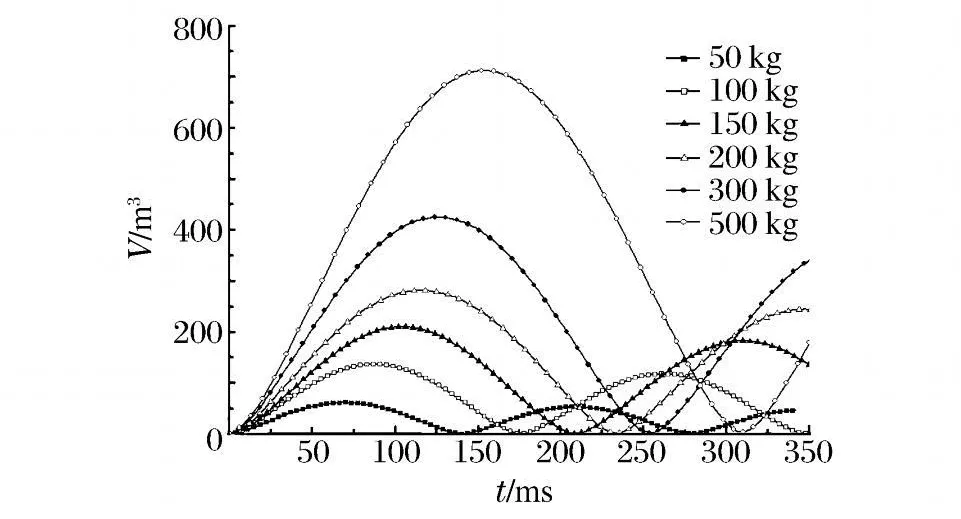
图6 气泡体积时间历程曲线Fig.6 Volume-time curves of bubbles under different charges
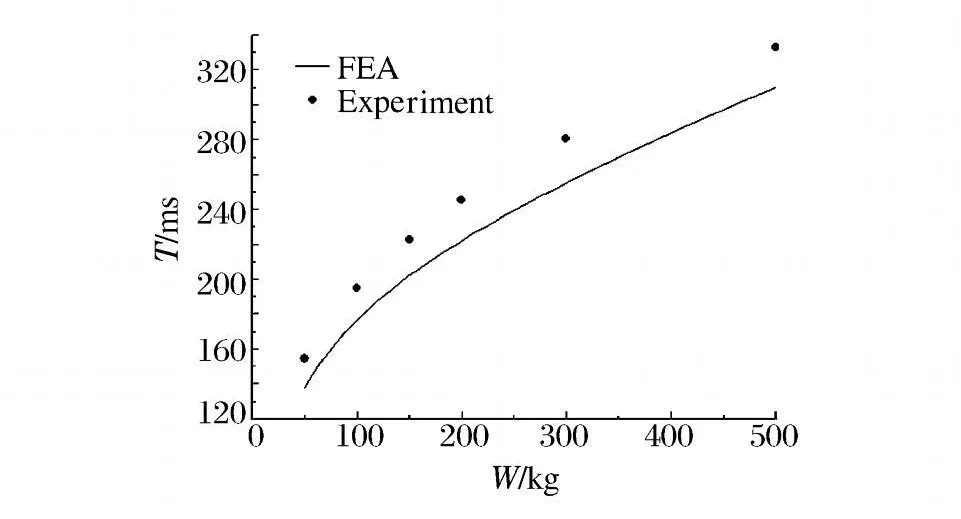
图7 不同装药量时气泡周期Fig.7 Period of bubbles under different charges
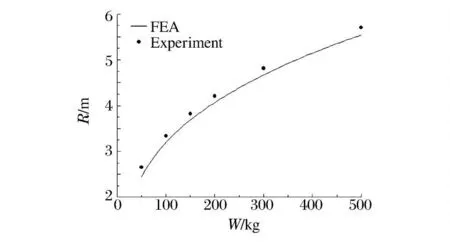
图8 不同装药量时气泡最大半径Fig.8 Maximal radius of bubbles under different charges
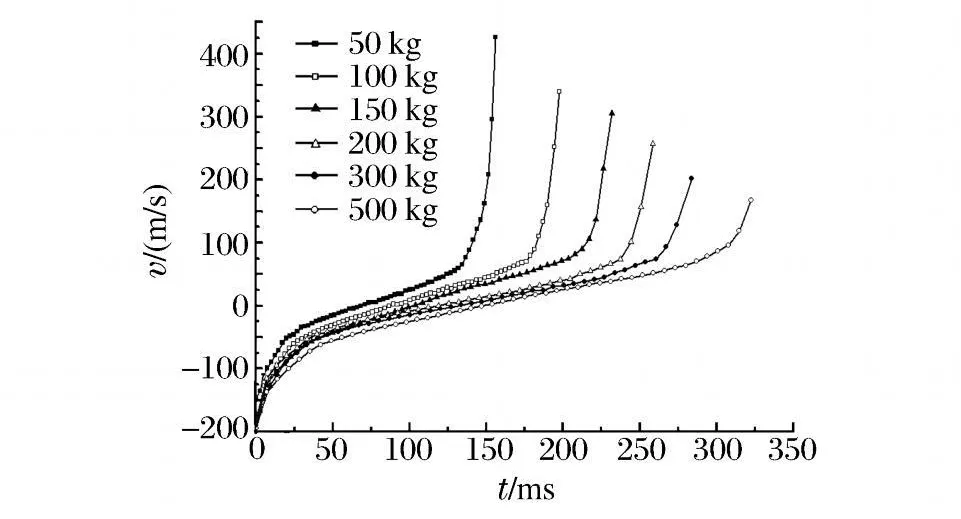
图9 气泡射流速度时间历程曲线Fig.9 Velocity-time curves of jets under different charges
3.2 水深对气泡动态特性的影响
为了考察水深的变化对气泡动态行为的影响,假定系列工况药量均为100 kg,爆炸水深从25 m 变化到125 m,计算不同水深情况下气泡体积、脉动周期、最大半径以及射流速度。各工况下气泡脉动以及射流形成过程与图5 类似。计算结果如图10 ~13 所示。
从图10 中可以看出,随着水深的增加,气泡各脉动周期内所对应时刻处的体积会不断减小。根据图10 中气泡体积变化,提取出气泡脉动周期,并将计算结果与经验公式进行对比,对比结果如图11 所示。从图中可以看到,气泡脉动周期随着爆心初始水深的增加而减小,计算结果与经验公式的误差较小。根据图10 中第1 次脉动周期内气泡最大体积计算出气泡等效半径,如图12 所示。从图中可以看出,随着水深的增加,气泡的最大半径同样会有所减小,对比计算结果与经验公式,二者具有较好的一致性,平均误差在4%左右。
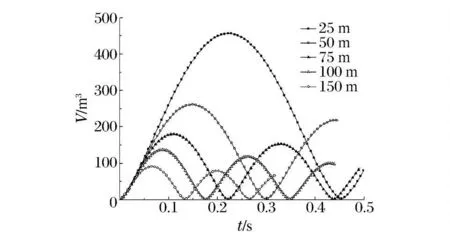
图10 气泡体积时间历程曲线Fig.10 Volume-time curves of bubbles at different depths
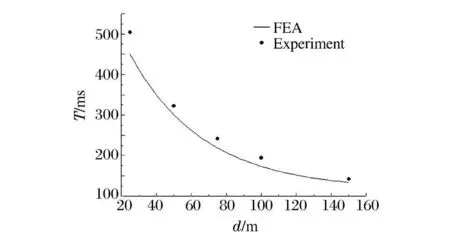
图11 不同水深时气泡周期Fig.11 Periods of bubbles at different depths
图13 为药量相同、爆心初始位置不同情况下,气泡正下方壁面运动速度的时间历程曲线。从图中可以看到,射流速度随着水深的增加而增加。也就是说,水越深,气泡射流载荷的局部效应越明显;相反,近水面爆炸所产生的气泡射流载荷速度降低,但射流影响区域变宽,因而总体破坏效应变明显。所以深水爆炸和浅水爆炸时气泡载荷对结构的破坏机理不同。深水爆炸气泡坍塌所产生的射流载荷能引起水中结构的局部破坏,而浅水爆炸泡射流载荷由于影响区域很宽,可引起结构的总体破坏。
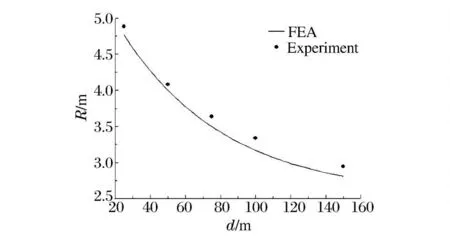
图12 不同水深时气泡最大半径Fig.12 Maximal radii of bubbles at different depths
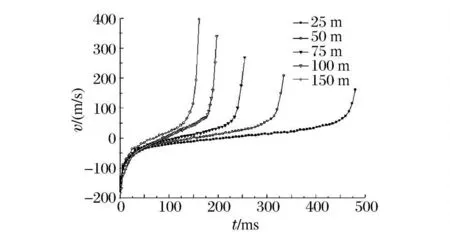
图13 气泡射流速度时间历程曲线Fig.13 Velocity-time curves of jets at different depths
4 结 论
基于气泡体积加速度模型,采用FORT RAN 语言开发了定义流场初始条件和边界条件的子程序,并结合MSC.DYTRAN 非线性有限元软件对水下爆炸气泡在自由水域中的运动特性进行数值模拟,计算结果与实验结果具有较好的一致性。分析总结不同水深及不同装药量等多种工况下水爆炸气泡动态特性,得到了以下主要建议及结论。
(1)水下爆炸包括装药的爆轰、冲击波的产生与传播、气泡的形成及脉动,三者虽然时间尺度上具有较大差异,但三者在时间上具有连续性,基于流场压力分布提出的气泡体积加速度适合于计算水下爆炸气泡初始条件的确定。
(2)基于MSC.DYTRAN 非线性有限元软件下开发的定义流场初始条件和边界条件的子程序EXINIT 和EXFLOW2,可以准确的计算出水下爆炸气泡脉动的全物理过程,且满足计算精度要求。
(3)气泡的运动体积、最大半径及周期随着装药量的增加而增加,变化范围较大;但随着装药量的增大,气泡射流速度减小,持续时间长。即小药量药包的气泡坍塌所产生的射流可能对结构造成局部毁伤,而大药量药包气泡坍塌所形成的射流速度相对较低,但射流影响区域很宽,对舰船结构造成总体破坏。
(4)气泡体积、最大半径以及脉动周期随着水深的增加而减小,且变化较大。随着水深的增大,气泡坍塌所产生的射流速度增大,持续时间短,即水越深,气泡射流载荷的局部效应越明显,能够造成水中结构的局部毁伤;水越浅,气泡的射流载荷速度相对较低,射流影响区域变宽,持续时间长,对水中结构的总体破坏效应越明显。
[1] Blake J R, Taib B B,Doherty G.Transient cavities near boundaries.Part I:Rigid boundary[J].Journal of Fluid Mechanics,1986,170:479-497.
[2] Chan P C, Kan K K,Stuhmiller J M A.Computational study of bubble-structure interaction[J].Journal of Fluids Engineering,2000,122:783-790.
[3] Blake J R, Gibson D C.Cavitation bubbles near boundaries[J].Fluid Mechanics, 1987,19(1):99-123.
[4] Wang Q X,Yeo K S, Khoo B C, et al.Nonlinear interaction between gas bubble and free surface[J].Computers and Fluids, 1996,25(7):607-628.
[5] Zhang Y L, Yeo K S, Khoo B C, et al.Three-dimensional computation of bubbles near a free surface[J].Journal of Com putational Physics, 1998,146(1):105-123.
[6] Wang C, Khoo B C.An indirect boundary element method for three-dimensional explosion bubbles[J].Journal of Computational Physics,2004,194(2):451-480.
[7] Klaseboer E, Hung K C,Wang C,et al.Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure[J].Journal of Fluid Mechanics,2005,537:387-413.
[8] Klaseboer E, Khoo B C,H ung K C.Dynamics of an oscillating bubble near a floating structure[J].Journal of Fluids and Structures, 2005,21:395-412.
[9] Pearson A,Cox E,Blake J R,et al.Bubble interactions near a f ree surface[J].Engineering Analysis with Boundary Elements, 2004,28:295-313.
[10] Zong Z.A hydroplastic analysis of a free-free beam floating on w ater subjected to an underw ater bubble[J].Journal of Fluids and St ructures, 2005,20:359-372.
[11] Takada N,Misawa M, Tomiyama A,et al.Numerical simulation of two-and three-dimensional tw o-phase fluid motion by lattice Boltzmann method[J].Computer Physics Communications,2000,129:233-246.
[12] Zong Y X, Reginald B H.An improved model for bubble formation using the boundary-integral method[J].Chemical Engineering Science,2005,60(1):179-186.
[13] Frost P A, H arper E Y.Acoustic radiation from surfaces oscillating at large amplitude and small mach number[J].The Journal of the Acoustical Society of America,1975,58(2):318-325.
[14] Hunter K S.Global-shape-function models of an underw ater explosion bubble[D].Boulder:University of Colorado,2001.
[15] Geers T L, Hunter K S.Pressure and velocity fields produced by an underw ater explosion[J].The Journal of the Acoustical Society of America, 2004,115(4):1483-1496.
[16] Hunter K S,Geers T L.An integrated wave-effects model for an underw ater explosion bubble[J].The Journal of the Acoustical Society of America,2002,111(4):1584-1601.
[17] Cole R H.Underw ater explosions[M].US:Princeton University Press,1948.

