邻近爆破对矩形岩柱稳定性影响的突变理论分析*
闫长斌,王泉伟,李国权,符新阁,左宇军
(1.黄河勘测规划设计有限公司,河南 郑州450003;2.大连大学材料破坏力学数值实验中心,辽宁 大连430071)
1 引 言
矩形岩柱是地下开采方式中常用的岩柱布置型式之一。岩柱可以有效地维持采场和采空区顶板及围岩的稳定性。实践表明,岩柱失稳往往会导致地下采场或采空区的整体破坏,甚至造成更严重的关联失稳[1]。岩柱的完好程度是判断地下采场和采空区稳定性的重要标志[2-3]。地下采场或采空区稳定性取决于顶板与岩柱,对岩柱稳定性进行的研究分别从现场测试[2]、数值计算[4-5]和可靠性[6]等方面入手,已取得丰硕的研究成果,但往往只考虑静荷载的作用和影响。事实上,由于爆破药量较大,井下生产爆破对邻近岩柱稳定性的影响不可忽视。在岩柱优化设计时,考虑爆破动载的影响,更符合生产实际、更安全可靠[7]。
岩柱失稳是一个非连续、非线性现象,应用突变理论方法分析是可行的。李江腾等[8]、潘岳等[9]运用尖点突变原理,基于势能原理,分析了岩柱失稳机理,但没有涉及爆破动载对岩柱稳定性的影响。由于爆破损伤作用的复杂性,爆破动载对岩柱稳定性的影响,既与爆破规模、爆破方法等因素有关,又与岩柱的物理力学性质有关[10-11]。爆破动载对岩柱稳定性影响的研究方法以实测或模型实验等手段为主[12]。应用突变理论方法分析爆破动载作用诱发岩柱失稳机理的研究成果报道较少。
2 非线性动力学模型
假定矩形岩柱的长度为a,厚度为h,高度为l,如图1(b)所示。由于岩柱的长度a 远大于厚度h,为了方便分析,忽略矩形岩柱在z方向上的变形,假定矩形岩柱的挠度发生在y 方向,且仅是x 和时间t的函数。取z方向上的单位长度进行矩形岩柱稳定性分析,即令a=1。此时,矩形岩柱的边界条件为:在x=0,l边为可移简支且作用有竖向压力P(0≤P≤Pcr),在z=0,a边为不可移简支。

图1 矩形岩柱的力学模型Fig.1 Mechanical models for a rectangular rock pillar
考虑岩柱失稳破坏时间效应时,借鉴粘弹性矩形板的非线性振动理论研究岩柱在爆破应力波扰动作用下的失稳问题。根据弹性动力学理论,各向同性Voigt粘弹性矩形板的非线性动力方程为[13-14]
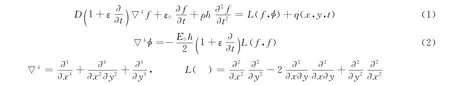
根据上述边界条件可知,矩形岩柱在z方向单位伸长为0。
假设式(1)的解及爆破扰动力为[13-14]

利用Galerkin原理,且量纲一化后,可得到
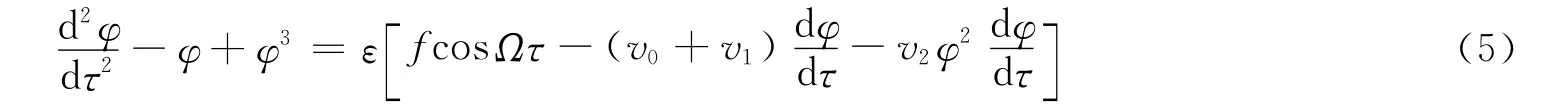
“已经摔死了十七个匠人了,”带领他们在舟中引眺的剑南节度使说,“真正凿到佛足,可能还需要一个甲子的工夫。”
根据上述各关系式,可将方程(5)的解设为以下形式

式中:H1是矩形岩柱的振幅,φ1是由于阻尼引起的响应滞后。
将H 视为时间不变量,再将式(6)代入式(5)中,略去谐波的高次项,并令sinΩτ 和cosΩτ 项前的系数在等式两边分别相等,可得

由式(7)~(8)可得
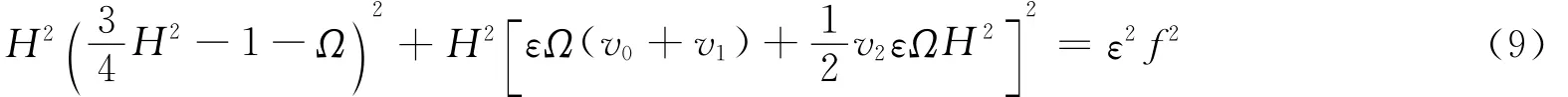
对上式作微分同胚变换[15-16],消去式(9)中关于H2的2次项得到
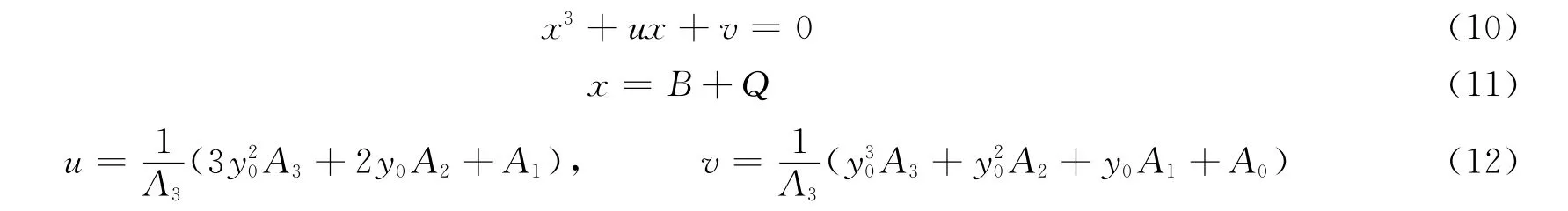
式(10)即为标准的尖点突变的平衡曲面方程。由于状态变量x 本身由2个变量组成,实际上式(10)也是双尖点突变模型。由突变理论[15-16]可知,爆破扰动作用下矩形岩柱失稳的必要条件为

爆破扰动作用下矩形岩柱失稳的充分条件为

将式(12)代入式(14)后可得

3 突变理论分析
根据式(11)~(15)及以上分析结果,难以直接看出各种爆破参量变化对矩形岩柱失稳机理的影响。下面分析竖向压力P、爆破扰动强度q0以及爆破扰动频率ω0对矩形岩柱失稳机理的影响。
3.1 爆破扰动强度对矩形岩柱稳定性的影响
矩形岩柱的有关参数分别为:a=1 m,l=10 m,h=1 m,m=n=1,μ=0.4 m,ρ=2t/m3,E0=6GPa,η=90 MPa·s,ε=0.015s,ω0=85rad/s,ε0=0.015,P=6,12 MN。由式(13)~(14)可知,u 和4u3+27v2可以反映岩柱的稳定程度。将以上参数代入,可得4u3+27v2随爆破扰动强度q0的变化规律,如图2所示。由图2不难看出,随着爆破扰动强度的不断增大,4u3+27v2呈现降低趋势;当P=12MN时,若爆破扰动强度q0增至33.5MN,则4u3+27v2等于0,此时满足岩柱失稳条件。另外,竖向压力P 越大,4u3+27v2越接近0,即满足岩柱失稳条件对应的爆破扰动强度q0越小。竖向压力P 越大,邻近爆破扰动作用下,矩形岩柱越容易发生失稳破坏。
3.2 爆破扰动频率对矩形岩柱稳定性的影响
矩形岩柱的有关参数分别为:a=1 m,l=10 m,h=1 m,m=n=1,μ=0.4 m,ρ=2t/m3,E0=6GPa,η=90 MPa·s,ε=0.015s,q0=35 MN,ε0=0.015,P=6 MN。将以上参数代入,可得u 和4u3+27v2随爆破扰动频率ω0的变化规律,如图3所示。由上述分析可知,要使矩形岩柱发生动力扰动失稳破坏,必须满足必要条件式(13)。由图3(a)中可见,爆破扰动频率必须满足一定的范围,在某一区间ω01≤ω0≤ω02,u大于0,爆破扰动作用下矩形岩柱不会发生失稳破坏。由图3(b)中可见,在竖向压力P作用下,爆破扰动频率必须大于某ω03时,才能满足式(14),即岩柱失稳。根据上述分析可知,若增大竖向压力P,爆破扰动作用下矩形岩柱发生失稳的可能性增大,而此时能够满足条件式(14)的爆破扰动频率ω03必然减小。
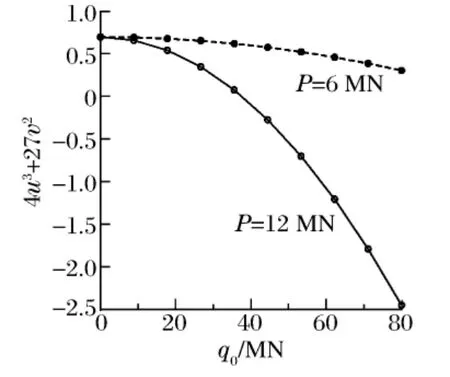
图2 4u3+27v2 随爆破扰动强度的变化Fig.2 Variation of 4u3+27v2 with blasting strength

图3 u和4u3+27v2 随爆破扰动频率的变化Fig.3 Variation of uand 4u3+27v2 with blasting frequency
4 结 论
运用突变理论研究了爆破震动对矩形岩柱稳定性的影响,得到了以下主要结论。
(1)在一定的爆破扰动强度和频率范围内,岩柱的动力响应可越过临界平衡位置,使得结构发生振幅(位移)突跳。邻近爆破扰动诱发矩形岩柱失稳破坏是一个不可逆的过程。岩柱对爆破震动荷载的动力响应具有滞后特性,即爆破动荷载频率变化路径对结构的振动特性有重要的影响。
(2)在考虑自重荷载的情况下,爆破震动是否会诱发矩形岩柱产生失稳不仅取决于爆破震动强度和频率,还与爆破扰动次数、结构自重荷载、上覆岩层荷载、采动应力、水平地应力、岩体物理力学性质以及结构的其他内部属性有关。
(3)随爆破扰动强度q0的增大,参数4u3+27v2呈现降低趋势,4u3+27v2越小,越容易满足失稳条件,岩柱越容易发生失稳破坏。
(4)竖向压力P 越大,满足岩柱失稳条件所对应的爆破扰动强度q0越小,矩形岩柱越容易发生失稳破坏。
(5)岩柱发生动力失稳破坏,爆破扰动频率必须满足一定条件。
[1] 姚宝魁,刘竹华,李春元,等.矿山地下开采稳定性研究[M].北京:中国科学技术出版社,1994:20-48.
[2] 刘沐宇,徐长佑.地下采空区岩柱稳定性分析[J].矿冶工程,2003,20(1):19-22.LIU Mu-yu,XU Chang-you.Stability analysis of pillars in mined-out area[J].Mining and Metallurgical Engineering,2003,20(1):19-22.
[3] 李元辉,南世卿,赵兴东,等.露天转地下境界岩柱稳定性研究[J].岩石力学与工程学报,2005,24(2):278-283.LI Yuan-hui,NAN Shi-qing,ZHAO Xing-dong,et al.Stability of boundary pillars for transition from open pit to underground mining[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(2):278-283.
[4] Kripakov N P,Sun M C,Donato D A.ADNIA applied toward simulation of progressive failure in underground mine structures[J].Computer &Structures,1995,56(2-3):329-344.
[5] Deng J,Yue Z Q,Tham L G.Pillar design by combining finite element methods,neural networks and reliability:A case study of the Fenghuangshan copper mine,China[J].International Journal of Rock Mechanics &Mining Sciences,2003,40:585-599.
[6] 刘学增,翟德元.岩柱可靠度设计[J].岩石力学与工程学报,2000,19(1):85-88.LIU Xue-zeng,ZHAI De-yuan.The reliability design of pillar[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(1):85-88.
[7] 杨伟忠,王勋业.控制岩柱破坏程度的爆破技术措施研究[J].金属矿山,1994,3:15-19.YANG Wei-zhong,WANG Xun-ye.Investigation on the blasting technical measures for controlling the ore pillar rupture degree[J].Metal Mine,1994,3:15-19.
[8] 李江腾,曹平.非对称开采时岩柱失稳的尖点突变模型[J].应用数学和力学,2005,26(8):1003-1008.LI Jiang-teng,CAO Ping.Cusp catastrophe model of instability of pillar in asymmetric mining[J].Applied Mathematics and Mechanics,2005,26(8):1003-1008.
[9] 潘岳,张勇,吴敏应,等.非对称开采岩柱失稳的突变理论分析[J].岩石力学与工程学报,2006,25(增刊2):3694-3702.PAN Yue,ZHANG Yong,WU Min-ying,et al.Analysis of catastrophe theory for pillar destabilization in dissymmetric mining[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(Supple 2):3694-3702.
[10] 闫长斌.爆破作用下岩体累积损伤效应及其稳定性研究[D].长沙:中南大学,2006.
[11] 闫长斌,徐国元.动荷载诱发上下交叠硐室间顶柱失稳的突变理论分析[J].工程力学,2007,24(4):46-51.YAN Chang-bin,XU Guo-yuan.Analysis on instability of the top pillar between overlap underground chambers induced by dy-namic loadings with catastrophe theory[J].Engineering Mechanics,2007,24(4):46-51.
[12] 赵奎,万林海,饶运章,等.基于声波测试的岩柱稳定性模糊推理系统及其应用[J].岩石力学与工程学报,2004,23(11):1804-1809.ZHAO Kui,WAN Lin-hai,RAO Yun-zhang,et al.Fuzzy reasoning system of pillar stability based on sonic wave measurement and its application[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(11):1804-1809.
[13] 吴晓.屈曲粘弹性矩形板的非线性振动分岔[J].力学与实践,2001,23(1):41-43.WU Xiao.The nonlinear thermal vibration bifurcation of bucking viscoelastic rectangular plate[J].Mechanics in Engineering,2001,23(1):41-43.
[14] 彭凡,傅衣铭.粘弹性板的非线性动力稳定特性分析[J].固体力学学报,2004,25(1):115-118.PENG Fan,FU Yi-ming.Features of the nonlinear dynamic stability for viscoelastic plates[J].Acta Mechanica Solida Sinica,2004,25(1):115-118.
[15] Zeeman E C.Catastrophe theory[J].Scientific American,1976,234(4):65-83.
[16] Saunders P T.突变理论入门[M].凌复华,译.上海:上海科学技术和文献出版社,1983.

