基于神经网络的变速率非线性盲源分离ICA算法研究

张天瑜

(无锡市广播电视大学机电工程系， 江苏 无锡 214011)

0 前 言

数字信号处理是当今信息时代的一项核心技术，它在通信、计算机、图像处理、语音识别等众多领域得到了较为广泛的应用.数字信号处理中的一个关键部分是信号去噪，而盲源分离(Blind Source Separation, BSS)是近年来在信号去噪领域中的一个研究热点[1-3].盲源分离是指不使用训练数据，在对信号系统没有任何先验知识的情况下，对含有噪声的原始信号进行分离.由于盲源分离可以在缺乏训练序列，条件比较恶劣的通信环境中应用，因此，盲源分离比一般的信号去噪方法拥有更为广泛的应用场合.当信号系统属于线性系统时，盲源分离的效果比较理想.但是由于实际的信号系统大多属于非线性系统，这样由线性模型得到的盲源分离效果就会产生较大的误差，目前非线性盲源分离已经开始逐渐取代线性盲源分离.2001年，Hyvarinen A等人提出了独立成分分析(Independent Component Analysis, ICA)，独立成分分析从出现到现在虽然时间不长，然而无论从理论上还是应用上它正受到越来越多的关注[4,5].近年来，利用神经网络并通过独立成分分析来实现盲源分离已经引起了世界各国学术界以及通信业界的高度重视.传统的神经网络非线性盲源分离ICA算法的学习速率是固定的，当系统的噪声和迭代误差较大时，迭代参数需要很长时间才能收敛，从而影响盲源分离的效果.根据信噪比和迭代误差来调节学习速率，作者提出一种基于神经网络的变速率非线性盲源分离ICA算法，并将该算法应用于图像去噪中.仿真结果表明，与传统的神经网络非线性盲源分离ICA算法相比，该算法具有更好的盲源分离效果.

1 非线性盲源分离ICA算法的模型

ICA是一种用来从多变量(多维)统计数据里找到隐含的因素或成分的方法，被认为是主成分分析(Principal Component Analysis, PCA)和因子分析(Factor Analysis, FA)的一种扩展.对于盲源分离问题，ICA是指在只知道混合信号，而不知道源信号、噪声以及混合机制的情况下，分离或近似地分离出源信号的一种分析过程.非线性盲源分离ICA方法主要是线性化ICA的扩展，即在线性模型的基础上引入非线性运算.盲源分离算法的过程依次为线性模型求逆以及非线性模型求逆[6-8].在通信系统中，不同子信道之间的干扰以及器件等物理因素的干扰是用混合方程来描述的，非线性盲源分离ICA算法中的混合方程为：

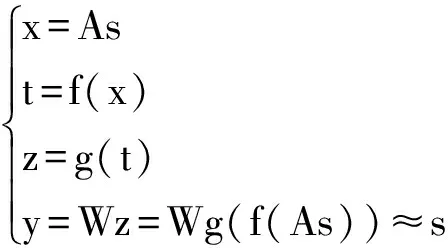
(1)

式中，s=[s1,s2,…,sN]T为源信号；x=[x1,x2,…,xN]T为线性混合模型；t=[t1,t2,…,tN]T为非线性混合后的观测信号；z=[z1,z2,…,zN]T为非线性解混合后的观测信号；y=[y1,y2,…,yN]T为经过线性解混合所得到的源信号的估计；f=[f1(x1),f2(x2),…,fN(xN)]T为非线性混合函数；g=[g1(t1),g2(t2),…,gN(tN)]T为非线性解混合函数；A为混合矩阵；W为分离矩阵.

非线性盲源分离ICA算法的结构如图1所示.

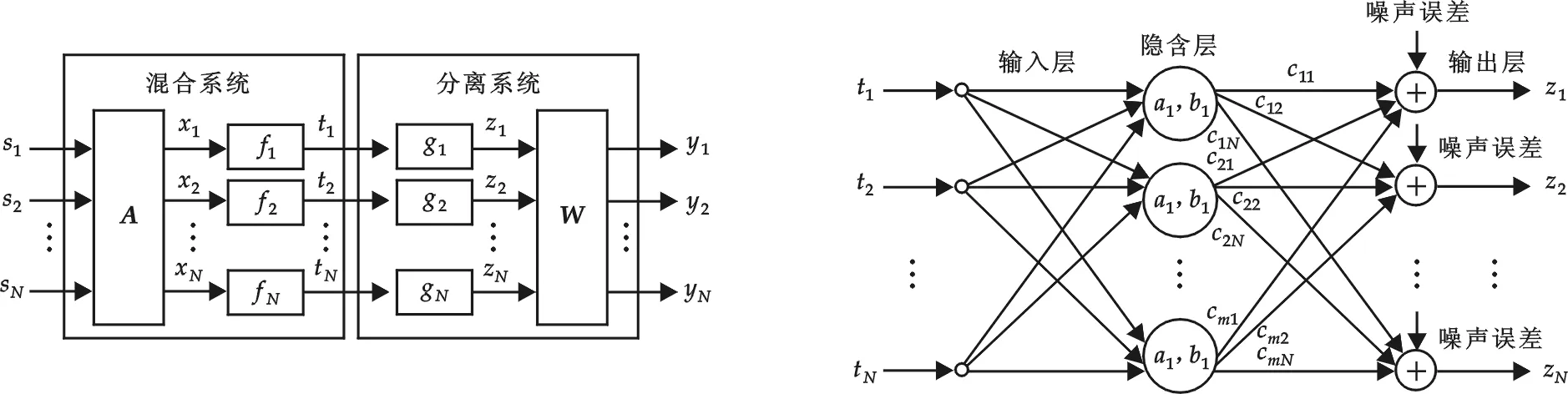
图1 非线性盲源分离ICA算法的结构 图2 基于RBF函数的神经网络模型

2 传统的神经网络非线性盲源分离ICA算法

传统的神经网络非线性盲源分离ICA算法的主要思路是利用多层感知器网络对非线性盲源分离ICA算法建立模型.研究表明，只要神经网络中的神经元足够多，该网络就能以任意精度近似任何非线性函数[9].在神经网络中，最常用的是径向基函数(Radial Basis Function, RBF)模型，基于RBF函数的神经网络模型如图2所示.

在图2中，神经网络中的RBF函数可以描述为：

y(t)=DK(t,p)

(2)

式中，p为隐含层参数，p=(a,b)，其中a和b为隐含层神经元信息，a=[a1,a2,…,aN]T，b=[b1,b2,…,bN]T；D为权重向量；K(t,p)为神经网络的核函数，它有多种形式，最常见的是高斯形式，即：

(3)

盲源分离的目的是恢复源信号，所以如果非线性解混合函数g是非线性混合函数f的反函数，则问题就变得相对容易.但是由于f是未知的，所以不能直接求得g.为了能够使得g近似f-1，需要引入衡量两者近似的指标函数，这可以采取最大互信息准则[10].

设非线性解混合函数的表达式为：

y(t)=g(t,ω)

(4)

在式(4)中，需要确定参数族ω，使得g→f-1，这里的ω对应于式(2)中的参数D、p，这可以通过最大互信息准则计算得到.

3 基于神经网络的变速率非线性盲源分离ICA算法

在图像去噪的过程中，图像传输的信噪比是一个重要的指标.当信噪比较大时，由于噪声图像与原始图像的误差较小，因此可以采用较大的学习速率使得迭代的参数尽快收敛到理想值；当信噪比较小时，由于噪声图像与原始图像的误差较大，因此可以采用较小的学习速率使得迭代的参数尽快收敛到理想值.另一方面，迭代误差也应该与学习速率有关.当迭代误差较大时，应该采用较大的学习速率，这样迭代参数可以尽快到达理想参数；当迭代误差较小时，应该采用较小的学习速率，这样迭代参数可以较为精确地收敛到理想参数.传统的神经网络非线性盲源分离ICA算法的学习速率是固定的，当系统的噪声和迭代误差较大时，迭代参数需要很长时间才能收敛，从而影响图像去噪的效果.为了提高图像去噪的效果，需要对传统的神经网络非线性盲源分离ICA算法进行改进.

基于神经网络的变速率非线性盲源分离ICA算法的步骤为：

第1步：基于RBF函数的神经网络模型，初始化参数D，a，b.

第2步：根据最大互信息准则，按照式(5)来更新参数D，a，b：

(5)

式中，C(ω)为对照函数；u(Δ,SNR)为学习速率；Δ为迭代误差；SNR为信噪比.

在式(5)中，u(Δ,SNR)的表达式为：

(6)

式中，SNR+和SNR-分别为信噪比的上界和下界；μ+和μ-分别为高低信噪比对于学习速率的贡献成分；λ1、λ2、λ3分别为迭代误差相对于学习速率的贡献比率.

第3步：设定迭代误差为：

(7)

则互信息加权误差为：

(8)

式中，Δpri为前一次迭代时的Δ.

第4步：

如果δ<ε，停止迭代，否则，重复第2步到第4步，其中ε为预先给定的较小的正数.

在图像去噪的过程中，噪声和图像数据之间一般都是相互独立的.传统的去噪方法是将图像数据和噪声一样对待，这会影响图像去噪的效果.而基于神经网络的变速率非线性盲源分离ICA算法可以得到相互独立的分量，并将独立的噪声数据从图像数据中去除，从而保证了原始图像的信息不被破坏.

4 仿真实验与结果分析

在通信系统中传输的信号采用标准的peppers(512×512)和Lena(512×512)作为原始图像，分别如图3和图4所示.在Matlab软件中对原始图像加入均值μ=0，方差σ=10的高斯白噪声，所得到的含噪图像如图5和图6所示.基于RBF函数的神经网络模型，分别采用基于传统的神经网络非线性盲源分离ICA算法和基于神经网络的变速率非线性盲源分离ICA算法，对含噪图像进行去噪的仿真实验，去噪后的图像分别如图7～图10所示.

图3 peppers原始图像 图4 Lena原始图像 图5 peppers含噪图像 图6 Lena含噪图像

为了对盲源分离的效果进行定量描述，采用原始图像和去噪后图像的相关系数作为盲源分离效果的综合评价指标.相关系数的定义为：

(9)

式中,DC为原始图像系数矩阵的离散余弦变换；DC′为去噪后图像系数矩阵的离散余弦变换.

改变高斯白噪声的噪声方差，采用原始图像和去噪后图像的相关系数作为去噪性能的综合评价指标，去噪后peppers图像和Lena图像的相关系数统计结果如表1所示.

表1 去噪后peppers图像和Lena图像的相关系数统计结果

通过图3～图10以及表1中数据的对比可以看出，由于引入了更为合理的学习速率，基于神经网络的变速率非线性盲源分离ICA算法去噪后的图像显得更清晰，在高斯白噪声的噪声方差不同时，所得到的相关系数比基于传统的神经网络非线性盲源分离ICA算法所得到的相关系数更大.由此说明，基于神经网络的变速率非线性盲源分离ICA算法具有更好的盲源分离效果.

5 结束语

针对传统的神经网络非线性盲源分离ICA算法中学习速率固定的缺陷，作者提出一种基于神经网络的变速率非线性盲源分离ICA算法，该算法的创新之处在于根据信噪比和迭代误差来调节学习速率.最后将该算法应用于图像去噪中，实现了良好的盲源分离效果，这在非线性盲源分离技术的应用领域具有一定的实用价值.

参考文献

[1] Chan T H, Ma W K, Chi C Y,etal. A convex analysis framework for blind separation of non-negative sources[J]. IEEE Transactions on Signal Processing, 2008,56(10):5 120-5 134.

[2] Erdogan A T. A simple geometric blind source separation method for bounded magnitude sources[J].IEEE Transactions on Signal Processing, 2006,54(2):438-449.

[3] Sidiropoulos N D, Davidson T N, Luo Z Q. Transmit beamforming for physical-layer multicasting[J]. IEEE Transactions on Signal Processing, 2006,54(6):2 239-2 251.

[4] Hyvarinen A, Karhunen J, Oja E. Independent component analysis[M]. John Wiley & Sons, New York, 2001.

[5] Roberts S J, Everson R. Independent component analysis: principles and practice[M]. Cambridge University Press, United Kingdom, 2001.

[6] Zarzoso V, Comon P. Robust independent component analysis by iterative maximization of the kurtosis contrast with algebraic optimal step size[J]. IEEE Transactions on Neural Networks, 2010,21(2):248-261.

[7] Gao J B, Xu Z, Lin H,etal. Independent component analysis based semi-blind I/Q imbalance compensation for MIMO OFDM systems[J]. IEEE Transactions on Wireless Communications, 2010,9(3):914-920.

[8] Klemm M, Haueisen J, Ivanova G. Independent component analysis: comparison of algorithms for the investigation of surface electrical brain activity[J]. Medical and Biological Engineering and Computing, 2009,47(4):413-423.

[9] Diamantaras K I, Theodoridis S, Pitas I. Second order Hebbian neural networks and blind source separation[C]. Eusipco: European Signal Processing Conference, Rhodes, Greece, 1998:1 317-1 320.

[10] Bell A J, Sejnowski T J. An information-maximization approach to blind separation and blind deconvolution [J]. Neural Computation, 1995,7(6):1 129-1 159.