基于MATLAB和有限元的虚拟振动试验系统
宋琼,范宣华,胡勇
(中国工程物理研究院 总体工程研究所,四川 绵阳 621900)
大型复杂试件的振动试验代价昂贵,为减小试验风险,有必要在正式开展试验前了解关键点响应,进行试验设计(包括合理选择控制方式和控制点等)。研究人员采用有限元软件对产品建模,选择激励点输入驱动力,计算产品的振动响应[1]。若需要了解不同激励点和不同输入驱动力下产品的响应,则需要重复进行复杂的有限元计算,需要花费大量时间。同时,由于仅采用有限元计算进行试验预估,忽略了振动台动圈、功率放大器和振动控制器等试验设备的影响,导致计算与实际试验状态存在差异。
笔者通过探讨振动台动圈、夹具以及试件一体化建模方法以及闭环的振动试验仿真系统,以期获得与真实试验系统更接近的仿真模型,并利用该系统进行试验辅助设计。
1 系统构建
采用有限元软件建立振动台动圈、夹具、试件一体化模型,通过仿真获得振动台动圈激励与试件响应的传递特性。采用MATLAB建立振动控制器和功放数学模型,以有限元仿真获得的传递特性作为被控对象导入控制器模型,形成闭环的虚拟振动试验系统,开展仿真试验,了解不同控制方式和控制点条件下,系统关键点的响应并开展试验设计。系统结构如图1所示。

图1 虚拟振动试验系统结构Fig.1 Structure of virtual vibration system
2 振动台动圈、夹具、试件一体化建模
试件传递特性的准确描述是本系统的关键技术之一。振动试验过程中,动圈电流和磁场作用产生驱动力,通过薄板连接螺钉传递至夹具及试件。由于动圈本身具有振动模态,不能作为一个质点考虑,为了准确描述振动试验中力的传递过程,将试件、夹具及振动台组成的整体结构进行有限元建模[1]。
采用有限元软件MSC.Patran 和MSC.Nastran,对振动台动圈部分进行有限元建模,并对边界条件进行模拟。动圈有限元模型如图2所示。

图2 动圈有限元模型Fig.2 The FEA model of armature
根据模态试验结果调整动圈3个部分的材料参数,使得振动台各部分的材料参数能够反映真实的材料特性。修正后,质量与实际质量一致,模态计算结果与模态试验结果比较接近,固有频率最大相对误差在4%以内。
将振动台有限元模型、夹具和试件有限元模型集成到动圈模型中,得到整个振动系统的有限元模型。通过开展相关试件的振动试验仿真研究,获得各关键点与振动台激励的传递特性,通过开展频域内的模型辨识获得传递函数。
3 振动设备建模
振动设备主要包括振动控制器、功放和振动台,是振动试验系统的加载系统,在虚拟试验系统中采用SIMULINK建立。
振动控制器作为控制系统,根据参考谱和试件响应完成功放驱动电压的生成和更新。主要环节包括:各通道PSD计算、控制PSD计算、误差计算、驱动谱更新、IFFT变换、帧搭接等。采用SIMULINK建立数字式开关功放模型,以振动台电阻和电感作为负载产生电流,与模拟的振动台磁场作用产生驱动力激励,完成驱动力产生的模拟。
4 仿真算例
为了验证随机振动仿真系统功能,以薄板作为试件,夹具底面连接动圈,上部与薄板试件相连,以此结构开展了有限元计算。薄板、夹具、试件的一体化有限元模型如图3所示。

图3 一体化试件有限元模型Fig.3 FEA model of integration test item
对整体模型驱动线圈部分施加一个恒定幅值的激振面力,激振频率范围为10~2 000 Hz,频率间隔为2.5 Hz,进行频率响应计算,根据控制点条件反推驱动线圈部分激振力大小。将反推得到的激振力谱以场的形式作用于驱动线圈,重复进行原频率下的测点响应计算,可得到给定试验条件下的测点仿真结果,进而获得测点与驱动力的传递序列。
导入MATLAB 开展模型辨识,获得各测点传递函数,辨识得到的各点传递函数如图4—图6所示。
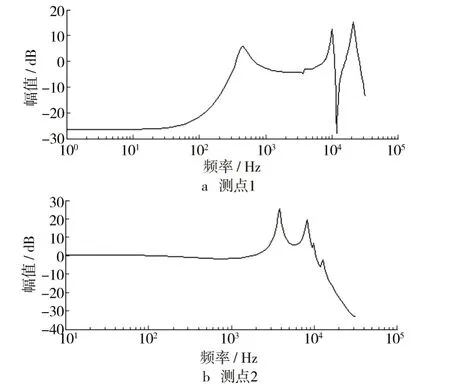
图4 薄板上测点的传递函数Fig.4 The transfer function of measure point on the plate
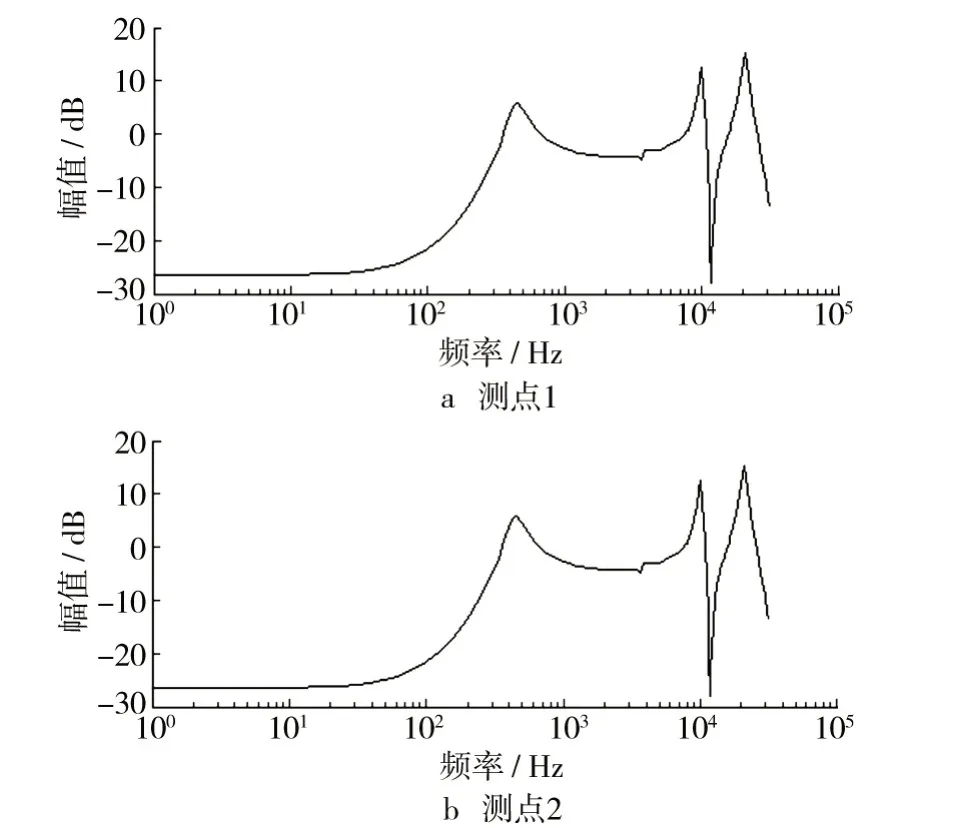
图5 台面上测点的传递函数Fig.5 The transfer function of measure point on the platform
4.1 单点控制仿真
以薄板上测点作为响应观测点,分别选取振动台台面、夹具上测点作为控制点,以图7所示PSD谱的参考谱开展仿真,结果如图8所示,所有仿真控制误差均小于1 dB。

图6 夹具上测点的传递函数Fig. 6 The transfer function of measure point on the fixture

图7 参考谱Fig.7 The reference PSD
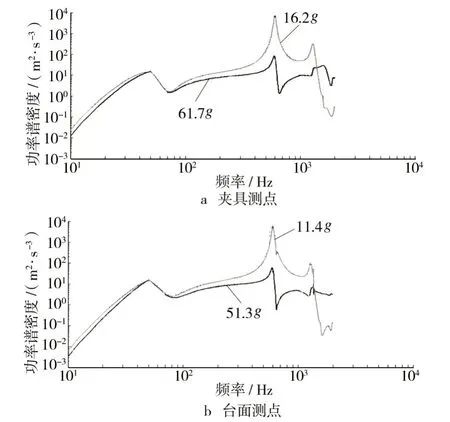
图8 控制点的薄板响应Fig.8 The response of the control point on sheet
以台面或夹具上的测点作为控制点,由于位置的差异测点2 的响应较大。薄板上的2 个测点的响应差异较大,在600 Hz 附近有1 个共振峰。选取台面或夹具上的测点作为控制点,薄板响应没有量级上的差异,说明夹具刚性较好。
4.2 两点平均控制仿真
分别在夹具和台面上各选取1个点作为控制点,开展2点平均控制,得到薄板上的2个测点的响应如图9所示,薄板响应与采用薄板测点作为控制点的响应差异很小,因此可以将台面和夹具的连接作为刚性连接考虑。选取夹具上测点1和薄板测点1作为控制点,开展平均控制,得到薄板响应如图9a所示。
选取薄板测点2和夹具测点1作为控制点,开展平均控制,得到薄板响应如图9b 所示,测点2 在600 Hz处的共振峰被削平出现了一个谷,说明在600 Hz处的驱动较小,有效地控制了控制点2的共振高度。
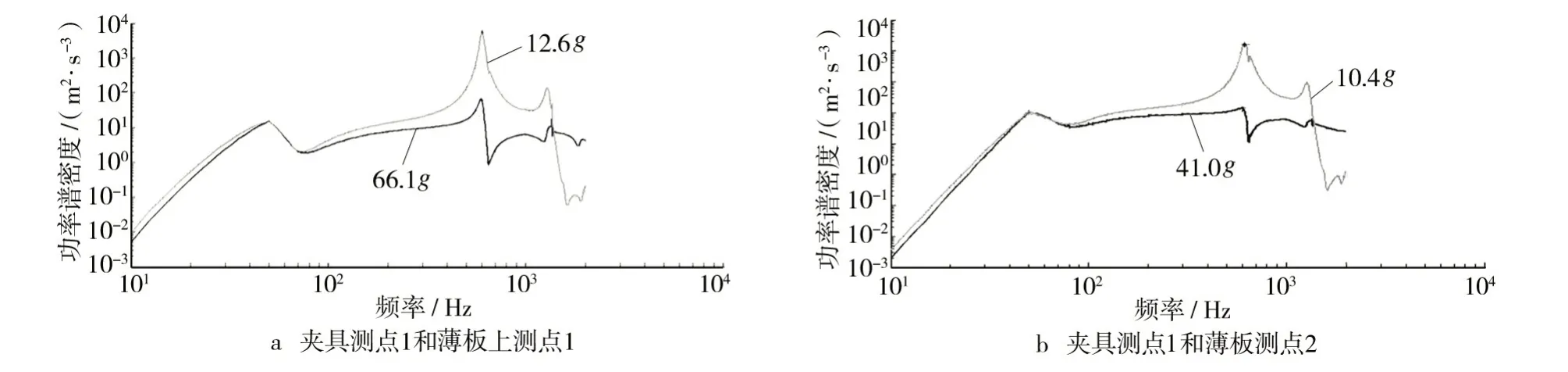
图9 测点平均控制结果Fig.9 The average control result of test points
5 结论
文中仿真算例模型线性度较好,因此试验结果与仿真结果一致性较好。对于复杂试件,有限元准确建模的难度较大,因此仿真结果与试验结果在高频段可能存在较大误差,但由于综合建立了振动控制器、夹具以及动圈模型,接近试验状态,仍旧可以对试验辅助设计起到很好的作用。
[1]范宣华,胡绍全.基于有限元法的电动振动台试验仿真研究[J].机械强度,2007,29(4):536—539.

