模糊控制技术在磁悬浮轴承中的应用研究

陈淳辉，孙从科，杨庆文

（海军蚌埠士官学校，安徽蚌埠233012）

磁悬浮技术属于自动控制技术，它是随着控制技术的发展而建立起来的。磁悬浮的作用，是利用磁场力使某一物体相对于基准框架保持固定位置。由于磁悬浮体与支撑部件之间没有任何接触，克服了由于摩擦带来的能量消耗和速度限制，具有长寿命、无污染、无噪声、低能耗、不受任何速度限制、安全可靠等优点。目前已广泛地开展磁悬浮轴承控制系统的理论研究。随着控制理论的不断完善与发展，采用先进的控制方法与算法，对磁悬浮轴承控制系统进行控制和设计，使系统具有更好的稳定性。特别是人工智能技术的产生，带来了磁悬浮控制系统向智能化方向快速发展。本文就模糊控制技术在磁悬浮轴承控制系统中的应用，作一些研究与探讨。

1 磁悬浮轴承系统的工作原理

磁悬浮轴承系统是由以下5部分组成：控制器，转子，电磁铁及线圈，传感器和功率放大器等。其中核心部件是控制器，控制器的性能基本上决定了整个磁悬浮轴承系统的性能。控制器的控制规律，决定了磁悬浮轴承系统的动态性能和稳定性。

磁悬浮轴承系统是一个非常复杂的机电一体化系统，用数学模型精确地描述是非常困难的，一般都采用在平衡点附近进行分析，再进行线性化处理。在不考虑五自由度之间耦合的情况下，本文仅对单自由度磁悬浮轴承系统的工作原理进行分析，如图1所示。

图1 单自由度磁悬浮轴承工作原理

系统工作原理是：电磁铁绕组中通以一定的电流，会产生电磁力，控制电磁铁绕组中的电流，使之产生的电磁力使转子可以悬浮在“空中”而处于平衡状态。但这种平衡状态是一种不稳定平衡，这是由于电磁铁与转子之间的电磁力大小与它们之间的距离成反比，只要平衡状态稍微受到扰动（如电压的波动等），就会导致平衡被破坏，因此必须对系统实行闭环控制。由位移传感器组成的测量装置，检测转子与电磁铁之间的距离变化。当转子在偏置电流I0的作用下处于平衡位置x0，若某时刻出现某一干扰fx，转子就会偏离平衡位置，偏移距离为x，为使转子回到平衡位置，须通过控制电流ic，使电磁铁Ⅰ的磁力减小，电磁铁Ⅱ的磁力增加。在不考虑重力等其它力的作用下，此时转子所受的力为

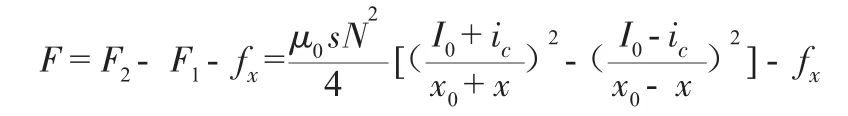
其中，

μ0为导磁率；

s为气隙截面积；

N为线圈匝数。

加在磁铁线圈上的电压经控制器调节、功率放大器放大处理后，电压减小，从而使电磁铁Ⅰ控制绕组中的电流相应减小，电磁力减小；使电磁铁Ⅱ电压增大，控制绕组中的电流相应增大，电磁力增大，转子被吸回平衡位置。反之亦然。从以上分析可知，该控制系统要实现对转子的稳定悬浮，其关键是设计一个具有良好调节作用、对外界干扰抑制能力强的模糊控制器。

2 模糊控制器的设计

基于模糊控制的磁悬浮轴承转子控制系统结构图如图2所示。

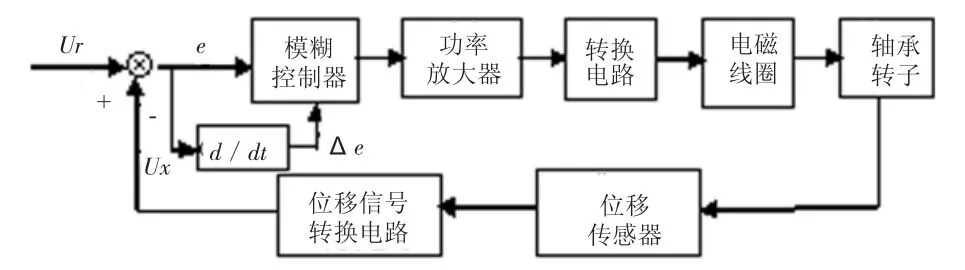
图2 磁悬浮轴承模糊控制系统

图中，

Ur为给定电压；

Ux为实测位移转换得到的电压；

e为电压偏差：e=Ur-Ux；

Δе为电压偏差变化率：Δе=d／dt；

u为模糊控制器的输出调节电压，此电压通过功率放大器放大，并转换成电流加在电磁铁线圈上。

模糊控制器的作用，是根据设定电压和实测位移转换得到的电压之间的偏差，经模糊推理输出调节电压，通过电路将电压转换电流，从而控制电磁铁线圈的电流大小，来实现转子的稳定悬浮。

本文采用查表法进行磁悬浮转子模糊控制器的设计。模糊控制器的硬件结构，将采用单片机来实现。因此，为了节约内存和运行时间，实际控制过程中不进行实时推理，而是离线计算输入、输出的对应关系，并以表格的形式存储在单片机的内存中，单片机根据实测输入值查询表格，得到相应的输出值。查表法设计模糊控制器按以下步骤进行：

2.1 模糊化

模糊化，是指将输入变量的精确值转化成适当论域上的语言变量值（即模糊输入值），即确定各输入、输出量的变化范围，及其对应语言变量的论域元素和量化因子K1、K2、K3。以实测位移转换得到的电压Ux和给定电压Ur的偏差e和偏差变化率Δе作为输入变量，控制器的输出电压u作为输出变量，取电压偏差e的基本论域[-10，l0]V，其语言变量E的论域为X=[-4，-3，-2，-1，0，1，2，3，4]，则偏差 E 的量化因子为 K1=4／10=2／5；偏差变化率Δе的基本论域为[-60，60]V／s，其语言变量 EC 的论域为 Y=[-4，-3，-2，-1，0，1，2，3，4]，则偏差变化率的量化因子K2=4／60=1／15；输出控制量的基本论域为 [-10，l0]V，输出语言变量U的论域 Z=[-4，-3，-2，-1，0，1，2，3，4]，则得到输出控制量的比例因子 K3=10／4=5／2。

2.2 模糊推理

模糊推理是指以知识库为基础，通过一定的推理机制，由模糊输入值得到模糊输出值的过程。考虑到实用的原则，输入变量和输出变量各为5个语言值：负大(NB)，负中(NS)，零(ZE)，正中(PS)，正大(PB)，输入及输出变量的隶属度函数均采用三角形，则语言变量论域上用以描述模糊子集（NB、NS、ZE、PS、PB）的隶属度函数如图3所示。

图3 输入、输出量的模糊定义

根据以往控制过程中的实践经验加以总结，得到采用“IF-THEN”形式的推理规则。当e为负大时，此时无论Δе的变化如何，为尽快消除偏差，应使控制量增加较快，所以控制量的变化取正大，即有

（1）IfE=NB And EC=PB Then U=PB；

（2）IfE=NB And EC=PS Then U=PB；

（3）IfE=NB And EC=ZE Then U=PB；

（4）IfE=NB And EC=NS Then U=PB。

当e为负小或0时，主要矛盾转化为稳定性问题。为了防止超调并使系统尽快稳定，根据偏差的变化率来确定控制量的变化。若Δе为正，表明偏差有减小的趋势，所以取较小的控制量。得到如下控制规则：

（5）IfE=NS And EC=ZE Then U=PS；

（6）IfE=NS And EC=PS Then U=ZE；

（7）IfE=NS And EC=PB Then U=NS；

（8）IfE=ZE And EC=ZE Then U=ZE；

（9）IfE=ZE And EC=PS Then U=NB；

（10）IfE=ZE And EC=PB Then U=NB。

若Δе为负，表明偏差有增大的趋势，所以要使控制量增加，须用如下控制规则：

（11）IfE=NS And EC=NS Then U=PS；

（12）IfE=NS And EC=NB Then U=PB

（13）IfE=ZE And EC=NS Then U=PS；

（14）IfE=ZE And EC=NB Then U=PB。

取得以上对应偏差为负或0时的控制规则后，根据系统的工作特点，当偏差为正时，也可得其相应的控制规则。由此可得到整个过程的所有控制规则，得到表1所示的控制规则表。

表1 模糊控制规则表

根据扎德模糊推理算法，采用“极大—极小值”法，得到控制量相应的模糊截集。然后把对应于当前输入值的所有有效规则推理得到的控制量的模糊截集进行“并”处理，再按重心法原则，对输出模糊量进行模糊判决得到控制量。构成模糊控制器的控制表（如表2所列）。

表2 模糊控制器的控制表

2.3 反模糊化

反模糊化是指由模糊输出值得到精确输出值的过程。由模糊控制规则表相应变化量的模糊值乘以比例因子K3，即得到控制量的精确输出值。

2.4 系统的模糊控制实现

（1）第一步是在每个控制周期中采集系统的输出U（K），求得实际偏差 e（K）和偏差变化率 Δе（K）：e（K）=Ux（K）-Ur（K），Δе（K）=e（K）-e（K-1）。

（2）第二步是将实际e（K）和Δe（K）分别乘以其对应的量化因子K1、K2，取得相应论域元素表征的查找控制表所需的Xi、Yi值，即：Xi=Kl×e（K），Yi=K2×Δe（K）e（K）。

（3）第三步是以Xi和Yi查找控制表的行和列，得到输出控制量的论域值Uij。

（4）第四步是将查表得到的控制量论域值Uij乘以比例因子K3，即u=K3×Uij，得到实际控制量u输出去控制被控对象。模糊控制器的控制表在单片机内存中是某一连续数据区，如要找到Uij，按照定位原则查得Uij的地址即可。

3 实验仿真分析

为了验证本文提出的设计方法，下面将对磁悬浮轴承转子的模糊控制系统进行仿真实验。控制对象选择实际控制任务中较常见的二阶加时延，设其传递函数为

二维模糊控制系统仿真模型框图如图4所示。

图4 二维模糊控制系统仿真模型图

偏差e和偏差变化率ec及控制器输出u的隶属函数，均取均匀分布的三角形隶属函数。在单位阶跃信号作用下，量化因子Ke=0.05，Kec=0.01以及比例因子Ku=1.25；所用模糊控制规则如表1所示（表格中为“空”表示无规则），得到系统输出波形如图5所示。在阶跃信号设定为5作用下，量化因子Ke=0.05，Kec=0.01以及比例因子Ku=6.25，得到系统输出波形如图6所示。

图5 单位阶跃信号作用下系统输出波形

图6 阶跃信号设定为5作用下系统输出波形

4 结束语

根据以上的仿真效果图，表明本文所设计的模糊控制器能够很好地控制转子的平衡问题。再经过多次调试，证明其系统工作稳定可靠，动态性能效果较好。该模糊控制系统和以往的模拟控制系统和数字控制系统相比，模糊控制器对于对象参数变化的适应性强，即系统具有较强的鲁棒性，具有一定推广价值。

[1]汤兵勇，林 吉.模糊控制理论与应用技术[M].北京：清华大学出版社，2002.

[2]张化光，希 勤.模糊自适应控制理论及其应用[M].北京：北京航空航天出版社，2002.

[3]张国良，曾 静，熙 政，方 林.模糊控制及其MATLAB应用[M].西安：西安交通大学出版社，2002.

[4]李国男.智能控制及其MATLAB实现[M].成都：电子工业出版社，2005.