“育鲲”轮测试数据处理及横摇建模的验证❋
惠小锁,张显库
(大连海事大学航海动态仿真与控制实验室,辽宁大连 116026)
0 引 言
21世纪是海洋的世纪,胡锦涛同志在 2006年首次提出中国要建立海洋强国的概念,从安全战略的高度提出了加强海上安全建设的必要性.如果视船体为刚体,则其在波浪中的运动可分解为横摇、纵摇、艏摇和纵荡、横荡、垂荡.其中又以横摇运动对航行安全的危害最大.20世纪 50年代末,日本学者野本谦作首次提出了目前船舶运动控制领域应用最为广泛的转艏操舵响应方程,也称作 Nomoto模型.1969年,Bech和 Wagner Smith又根据实际需要提出了非线性响应型模型(也称作非线性二阶野本模型).国内对船舶的响应型模型的研究也不是太多,主要成果见参考文献 [1-2],而对考虑横摇的船舶响应型数学模型的研究更是不多[3].本文通过把限幅滤波、算术平均滤波、低通滤波等数据滤波方法引入船舶横摇角数据的处理过程,借以降低噪声对横摇角信号的干扰,在船舶试验数据分析的基础上,结合理论讨论,建立了基于船舶回转试验的横摇响应型数学模型,并用育鲲轮的实船回转实验数据进行了验证.
1 测试数据处理技术
限幅滤波即根据实践经验确定出相邻两次采样信号之间可能出现的最大偏差值,若信号大于此偏差值,则表明该输入信号为干扰信号,应去掉或用上次值代替本次值;若小于此偏差值,可作为本次采样值[4].
算术平均滤波法就是连续取 N个采样值进行算术平均运算,N值较大时信号平滑度较高,但灵敏度较低;N值较小时信号平滑度较低,但灵敏度较高.
低通滤波是指允许信号中从零到低于低通滤波器通带上限频率(有时也称截止频率)的频率分量通过,而频率分量高于上限频率的频率分量则得到衰减[5].
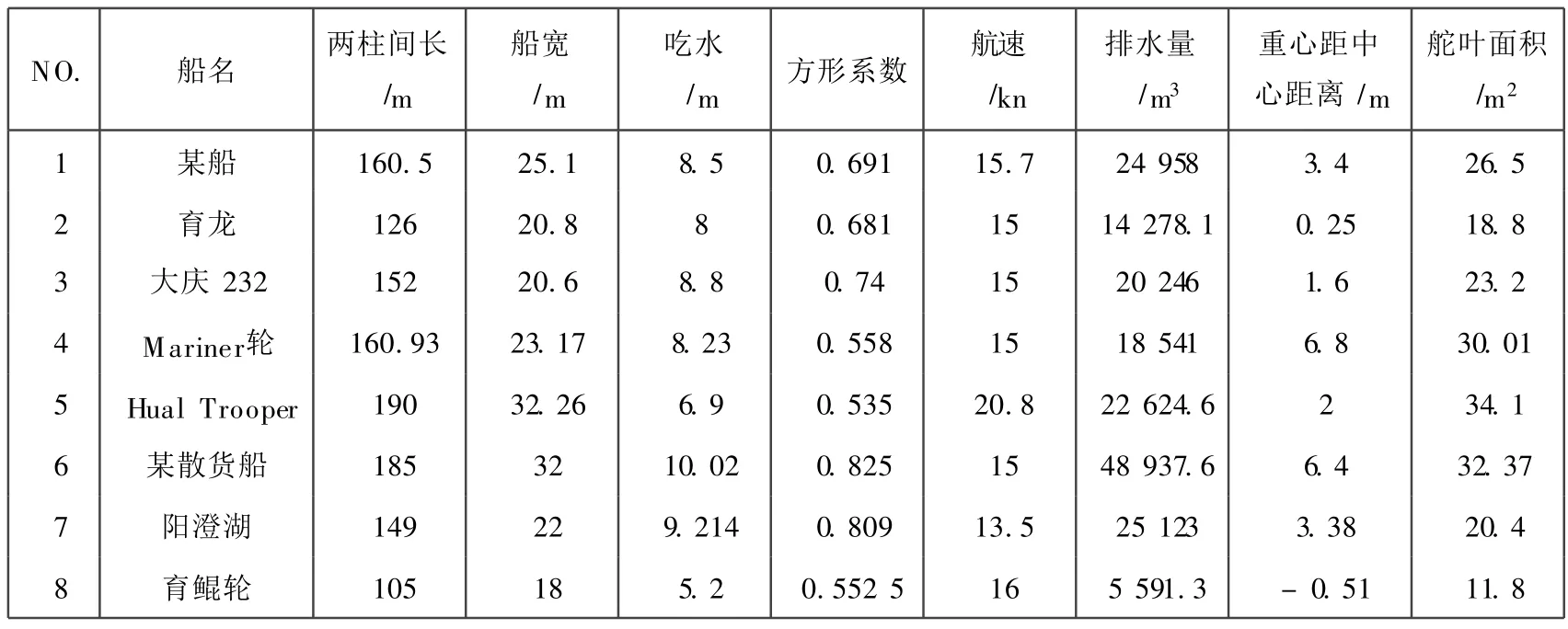
表1 船舶 8大参数列表Tab.1 Eigh t parameters of ships
表1给出了 8条船舶的 8大参数,采用文献 [3]给出的输入舵角W对于输出横摇角h的响应型数学模型

式中:K1,T1为待定系数,因为与船舶操纵性指数 K,T相类似所以称之为船舶横摇指数.显然从舵角W到横摇角h的响应型数学模型为典型的一阶惯性系统.取稳定旋回之后约 400 s时间内的横摇角的平均值为稳定的横摇角h,系统稳定时,K1=h/W,而 4T1的时间可以达到 0.982倍的稳定横摇[3],这样就可计算出船舶横摇指数 K1,T1.
通过 Matlab仿真,取采样时间为 1 s,可以得到 7条船分别在打 15°和 25°舵角进行旋回时候的两组横摇角数据,共 14组(由于数据太多,本文就不再给出).在仿真过程中为了更真实的模拟海上复杂的风浪流等影响,特地加入了白噪声干扰信号,而在数据处理的过程中为了力求准确首先应该对这些噪声进行限制,从而得到较为精确的结果.以某船在 25°舵角旋回时的横摇角数据(图1)为例,先后采用限幅滤波、算术平均滤波、低通滤波及三者的复合滤波编写程序处理[6],得到结果分别如图2~图4所示.
通过观察图2~图4可以发现,单纯的采用限幅滤波法和算术平均滤波法无法达到预期的平滑度和精度;而低通滤波法和包括限幅、算术平均、低通在内的复合滤波法都可以做到使横摇角数据曲线很平滑,但前者的精度比不上后者,具体比较结果如表2所示.

表2 低通滤波与复合滤波的精度对比Tab.2 Accu racy com parison betw een low pass filtering and com pound filtering
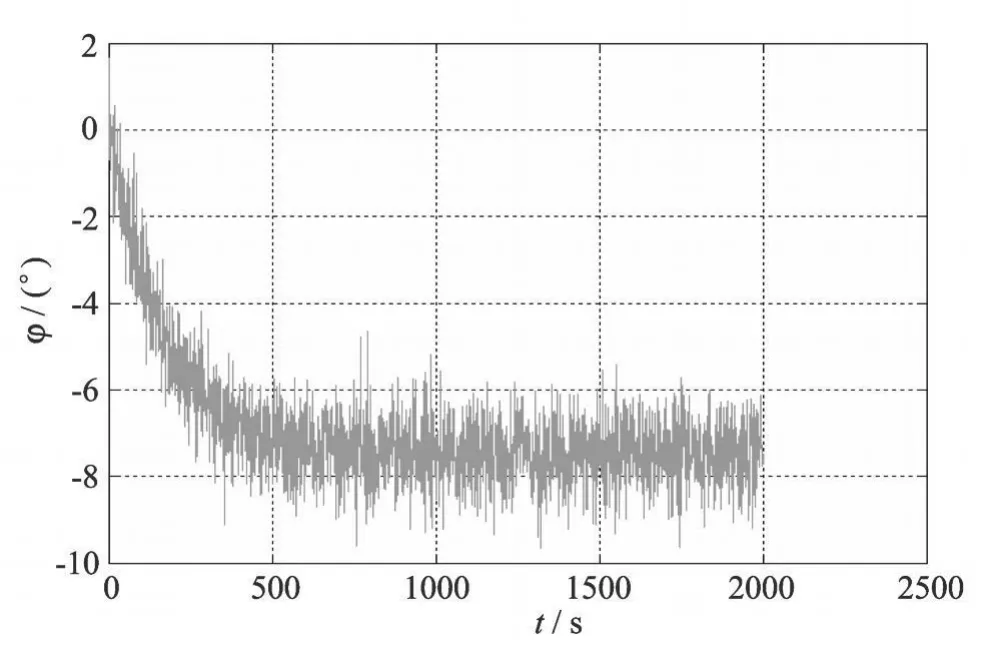
图1 某船 25°旋回时横摇角数据Fig.1 Test roll angle data of a ship(25°)
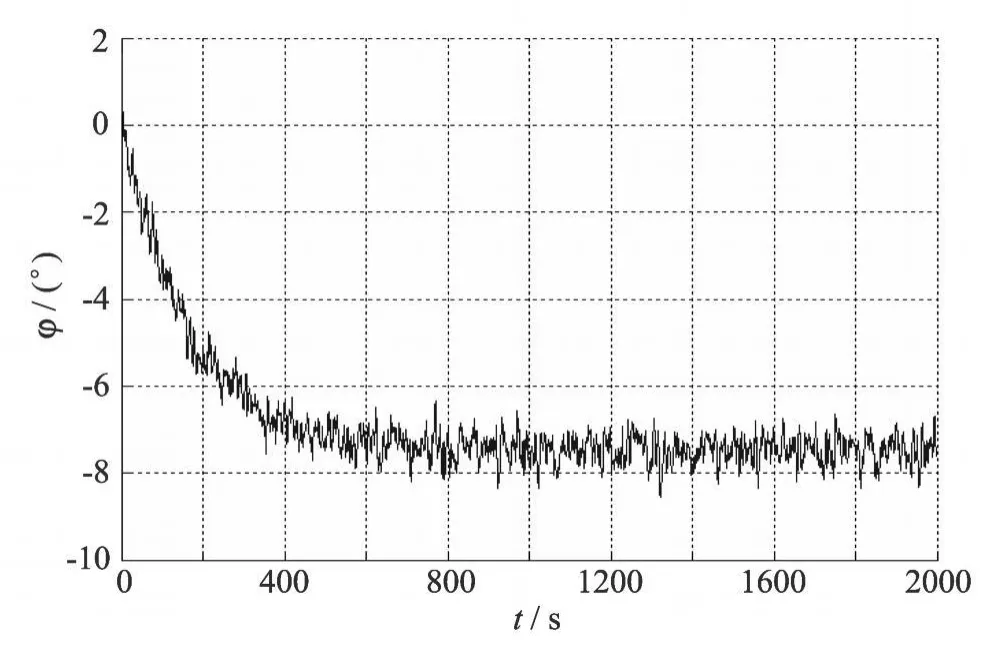
图2 经算术平均滤波处理后的某船 25°旋回时横摇角数据Fig.2 Test roll angle data of a ship(25°)after arithmetic average filtering
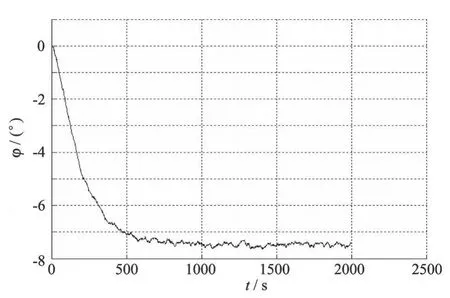
图3 经低通滤波处理后的某船 25°旋回时横摇角数据Fig.3 Test roll angle data of a ship(25°)after low-pass filtering
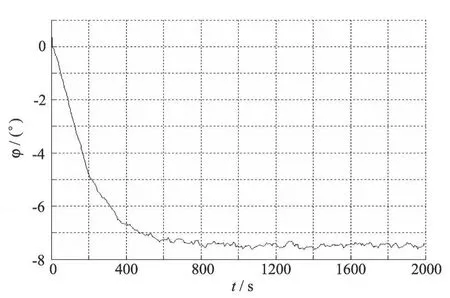
图4 经复合滤波处理后的某船 25°旋回时横摇角数据Fig.4 Test roll angle data of a ship(25°)after compound filtering
2 复合滤波法的应用及其精度分析
通过以上对比,知道复合滤波方法可应用到船舶横摇角数据的处理中.首先通过限幅滤波,剔除掉测量横摇角数据中误差特别大的一些点[7],然后通过算术平均滤波和低通滤波,使曲线变得更加平滑[8].取 7条船舶达到稳定旋回后约 400 s时间内的横摇角平均值为该船的在该角度下的横摇角,取每条船舶15°和 25°舵角旋回时的 K1,T1的平均值为该船最终的横摇指数 K1,T1,并给出 K1,T1的真值进行误差计算,结果见表3.
通过观察表3可以发现,经过复合滤波处理后得到的船舶横摇指数 K1与真值之间的误差值都小于1%,船舶横摇指数 T1与理论计算值之间的误差在 1.8%~16.1% 之间,说明这种利用包括限幅滤波、算术平均滤波、低通滤波在内的复合滤波方法处理横摇角数据的精度是较为理想的.
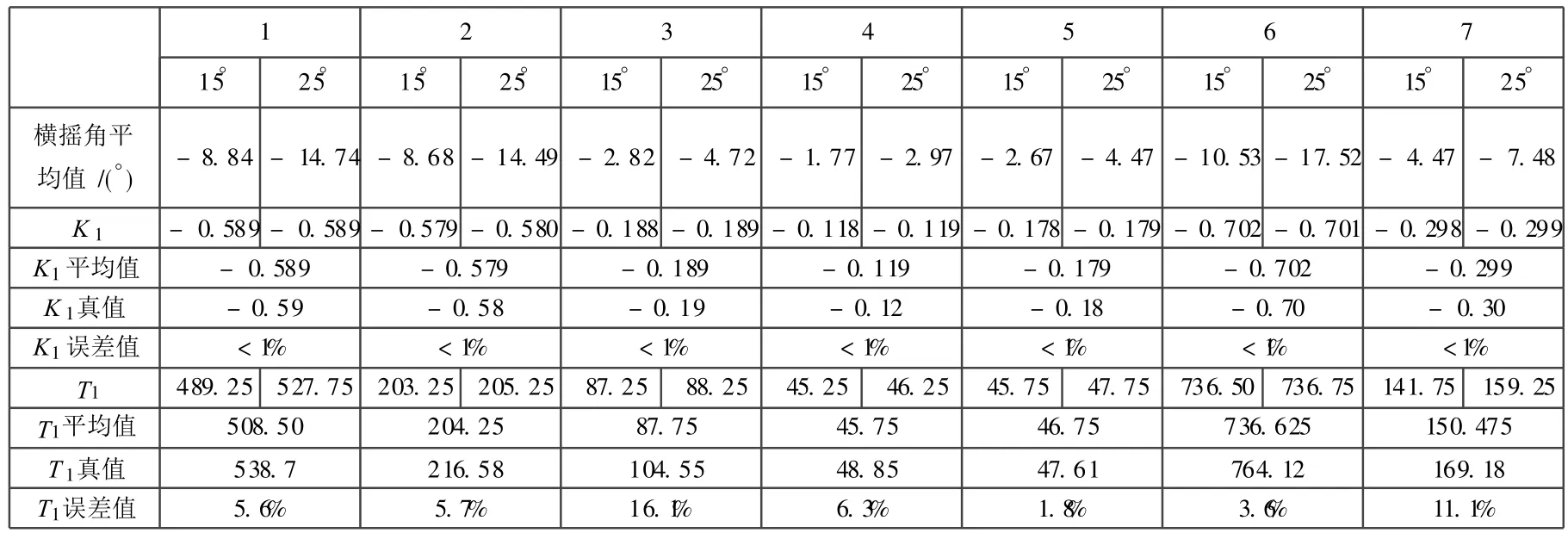
表3 7条船舶的横摇指数列表Tab.3 The list of the indexes of rolling for 7 ships
3 “育鲲”轮横摇测试数据处理及建模
“育鲲”轮实船实验时分别进行左右舵 5°旋回,直到稳定旋回.期间每隔 1 s记录一次旋回时的横摇角数据(图5和图7).用同样的复合滤波方法可以得到处理后的“育鲲”轮横摇角数据(图6和图8).
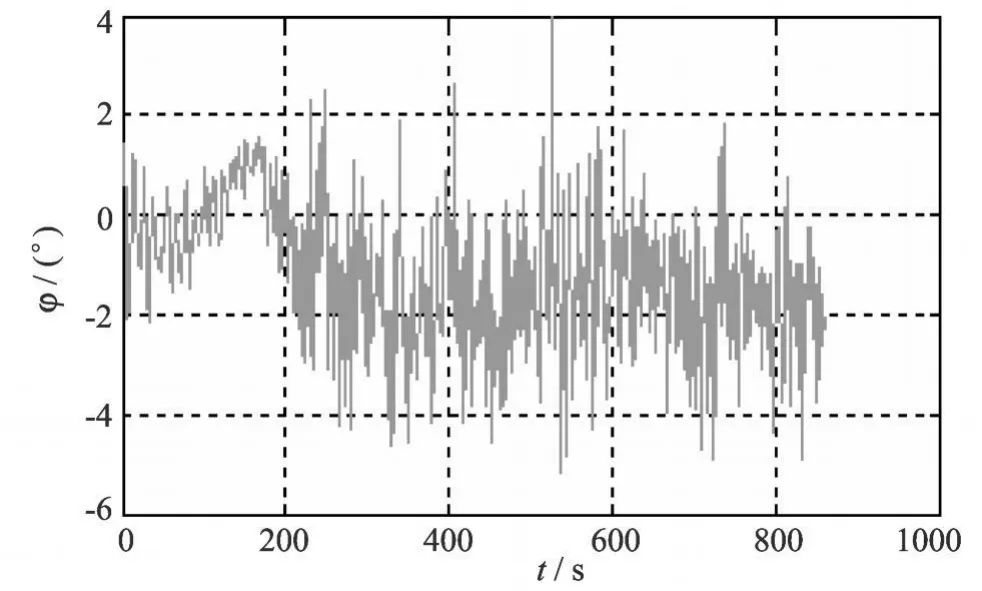
图5 “育鲲”轮右舵 5°旋回时横摇角数据Fig.5 Test roll angle data of YUKUN ship(starboard 5°)

图6 “育鲲”轮右舵 5°旋回时滤波后的横摇角数据Fig.6 Test rollangle data of YUKUN ship(starboard 5°)after filtering
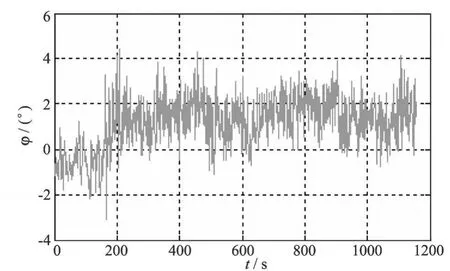
图7 “育鲲”轮左舵 5°旋回时横摇角数据Fig.7 Test roll angle data of YUKUN ship(port 5°)
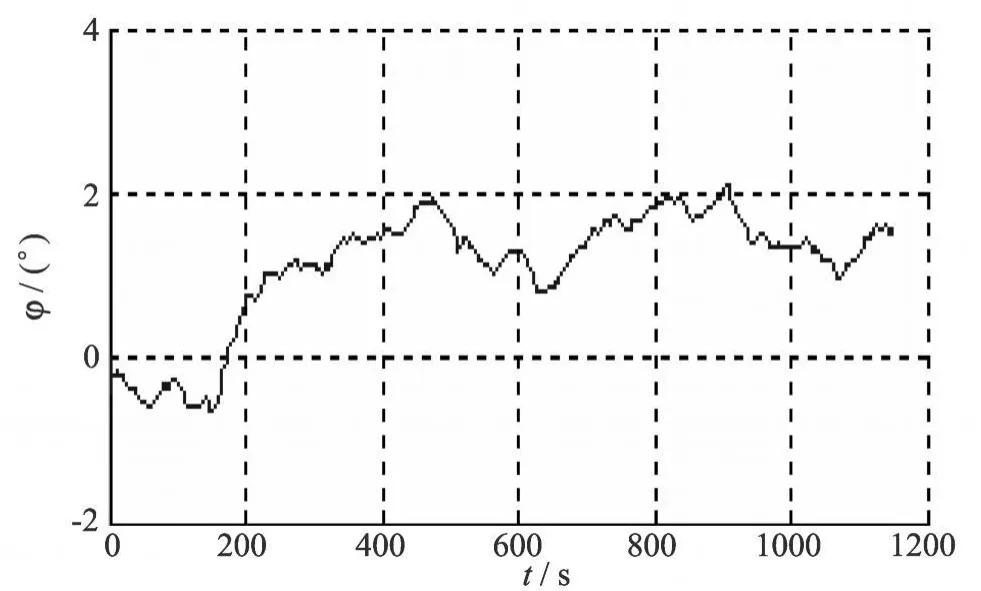
图8 “育鲲”轮左舵 5°旋回时滤波后的横摇角数据Fig.8 Test rollangle data of YUKUN ship(port 5°)after filtering
由于船舶在旋回初始阶段会出现内倾,故图6和图8中,在初始的 100~ 200 s左右的时间都会出现一个与横摇角角度变化趋势相反的过程[9].另外由于试验时海上存在 6级风,有浪,有流,所以船舶即使在稳定旋回时横摇角也很难维持在一个稳定的状态,会出现类似于图6和图8中的在稳定值附近波动的状态.且旋回试验所在的海域水深为 18m,稍微有点浅[9];这些因素都会影响船舶的回转和横摇效果,所以“育鲲”轮的回转横摇角数据曲线不如仿真实验的横摇角数据曲线平滑.但考虑到这些因素的影响,“育鲲”轮左右舵 5°旋回的横摇角数据都可以近似看成一阶惯性系统并利用文献[3]中的横摇模型来处理.
经过计算,可以得到“育鲲”轮的横摇指数为 K1=0.307,T1=83.8,见表4.由参考文献 [3]可知,用该论文里的计算方法所得“育鲲”轮横摇指数为 K 1=0.31,
T1=90.6.所以比较二者可得出横摇指数 K1的误差值为 0.3% <1%,横摇指数 T1的误差值为 7.42% <16.1%,进一步验证了包括限幅滤波、算术平均滤波、低通滤波的复合滤波方法在船舶横摇角数据的处理过程中的效果,也验证了文献[3]的结果是可信的.进而可以得到“育鲲”轮的响应型横摇数学模型[10]为

表4 “育鲲”轮左右舵 5°旋回时的船舶横摇指数Tab.4 The indexes of rolling of YUKUN ship w hen she is turning(port 5°and starboard 5°)

4 结 论
本文先对 7艘船舶进行了 15°和 25°旋回仿真,得到了 14组船舶横摇角仿真测试数据.通过与真值的对比分析,在验证了各种滤波的数据处理方法的精度后,将精度较高的包括限幅滤波、算术平均滤波、低通滤波的复合滤波方法应用于“育鲲”轮的实船实验横摇角数据的处理,分析了产生误差的原因并证明了该复合滤波方法的有效性及实用性,进而建立了“育鲲”轮的响应型横摇数学模型.该模型简单、便于分析.
[1] 张显库,金一丞.汽车运输船的响应型非线性数学模型[J].哈尔滨工程大学学报,2007,28(5):487-490.
Zhang Xianku,Jin Yicheng.Mathematicalmodel of nonlinear responding ship motion for car carrier[J].Journal of Harbin Engineering University,2007,28(5):487-490.(in Chinese)
[2] 张显库,贾欣乐,刘川.响应型船舶运动数学模型的构造 [J].大连海事大学学报,2004,30(1):18-21.
Zhang Xianku,Jia Xinle,Liu Chuan.Research on responding shipmotionmathematicalmodel[J].Journalof Dalian Maritime University,2004,30(1):18-21.(in Chinese)
[3] 张显库,杨佐昌,关巍,等.基于船舶回转实验建立横摇响应型数学模型[J].中国航海,2009,32(4):77-79.
Zhang Xianku,Yang Zuochang,GuanW ei,etal.Respondingmathematicalmodel for ship rollbased on ship turning test[J].Navigation of China,2009,32(4):77-79.(in Chinese)
[4] 宋寿鹏.数字滤波器设计及工程应用 [M].镇江:江苏大学出版社,2004:48-85.
[5] 程佩青.数字信号处理教程[M].北京:清华大学出版社,2001:102-138.
[6] 丁磊,潘贞存,丛伟.基于 M ATLAB信号处理工具箱的数字滤波器设计与仿真[J].继电器,2003,31(9):49-51.
Ding Lei,Pan Zhencun,Cong W ei.Design and simulation of digital filter based on Signal Processing Toolbox of MATLAB[J].Relay,2003,31(9):49-51.(in Chinese)
[7] 卓宁.靶场外弹道数据处理中野值点剔除方法 [J].测试技术学报,2008,22(4):313-317.
Zhou Ning.Study on outlier elim inating method for data p rocessing o f exterior trajectory[J].Journal o f Test and Measurement Technology,2008,22(4):313-317.(in Chinese)
[8] 安婷婷,张文梅.双通带带通滤波器的分析与设计[J].测试技术学报,2009,23(4):303-306.
An Tingting,Zhang W enm ei.Design and analysis of dual-band filter[J].Journal of Test and Measurement Techno logy,2009,23(4):303-306.(in Chinese)
[9] 洪碧光,杲庆林,汤国杰.船舶操纵[M].北京:人民交通出版社,2008:76-93.
[10] 张显库,杨佐昌,关巍,等.基于回转实验计算操纵性指数 [J].计算技术与自动化,2009,28(4):1-7.
Zhang Xianku,Yang Zuochang,Guan Wei,et al.Calculation ofmaneuverability indices based on ship turning test[J].Computing Technology and Automation,2009,28(4):1-7.(in Chinese)

