欠采样技术的超宽带信号子空间重建方法

杨 峰，胡剑浩，李少谦

(1. 电子信息控制重点实验室 成都 610036; 2. 电子科技大学通信抗干扰技术国家重点实验室 成都 611731)

欠采样技术的超宽带信号子空间重建方法

杨 峰1，胡剑浩2，李少谦2

(1. 电子信息控制重点实验室 成都 610036; 2. 电子科技大学通信抗干扰技术国家重点实验室 成都 611731)

针对超宽带脉冲信号采样中需要设计超高速模数变换器的问题，提出了一种带通采样结构和子空间重建算法。超宽带脉冲信号通过一个带通滤波器后，以数倍信号新息率进行采样，然后采用子空间重建算法可以准确地恢复出超宽带脉冲信号的幅度和时移。分析和仿真结果表明，该算法所要求的采样率低于传统香农采样定理要求的奈奎斯特率；当信号受到噪声影响时，子空间重建算法的性能优于现有的零化滤波重建算法。

带通采样; 新息率; 子空间重建; 超宽带

针对UWB脉冲信号的采样问题，本文提出了一种带通采样结构和子空间重建算法，该方法避免了传统香农采样定理所要求的最小奈奎斯特率采样，所要求的ADC采样率仅为UWB脉冲信号新息率的数倍；当UWB脉冲信号受噪声影响时，子空间重建算法的性能优于现有的零化滤波重建算法。

1 系统模型

UWB脉冲信号的数学表达式为：

式中 i为UWB信号数据帧中的第i个脉冲；p为UWB信号一帧中脉冲的个数；Ai为直接序列扩频伪随机序列；β⎣i/p⎦为PAM调制脉冲幅度；Tf为脉冲重复周期；ci为跳时扩频随机码；Tc为跳时扩频时移；δα⎣i/p⎦为PPM调制脉冲时移；g(t)为UWB脉冲信号波形，最常见的脉冲波形是高斯单脉冲。

将式(1)写为高斯单脉冲g(t)与冲激串信号x(t)的卷积有：

本文将探索如何按照信号新息率进行采样和重建UWB脉冲信号的方法，所提出的采样与重建系统结构如图1所示。

图1 系统结构

UWB信号s(t)通过一个带宽大于(等于)信号新息率的带通滤波器h(t)，以数倍信号新息率进行采样，将采样得到的离散时间信号y[n]变换到频域后，采用简单的迫零均衡算法获得冲激串信号x(t)的傅里叶变换X[k]。采用子空间算法求解冲激串信号的幅度di和时移ti，再根据式(2)准确地重建UWB信号。由于UWB信号的新息率ρ远远小于奈奎斯特率，因此本文算法所要求的采样率低于传统香农采样定理所要求的采样率。

2 子空间重建算法

根据图1中的系统模型，带通采样后离散时间信号y[n]的数学表达式可以写为[8]：

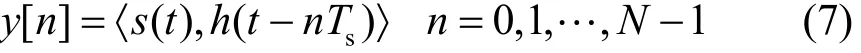
式中 h(t)为带通滤波器的冲激响应函数；Ts为采样时间间隔，当采样率大于信号新息率时，N≥2p；〈 · , · 〉为内积运算符。将带通滤波器h(t)中心频率fc设置为UWB脉冲信号具有最高频谱幅度处，可以获得最大信噪比，带通滤波器的带宽B大于信号新息率ρ 。

离散时间信号y[n]的傅里叶变换为：

经过迫零均衡后，可得到冲激串信号x(t)的离散傅里叶变换：

式中 G[k]为高斯单脉冲信号g(t)的离散傅里叶变换。

根据式(3)，冲激串信号x(t)的傅里叶变换为：

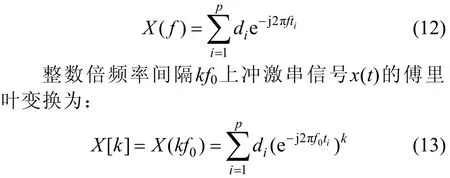
从式(14)可以看出，ui包含了冲激串信号x(t)的时移信息ti，因此求解ui，就可以得到冲激串信号的时移ti。

考虑由X[k]构成的汉克尔矩阵有：

以不同的采样率(如2倍、4倍或8倍信号新息率)对带通滤波后的UWB信号进行采样，得到的离散时间信号y[n]的点数N是不同的，因此由X[k]构造的汉克尔矩阵H具有不同的维数。通过提高采样率，可以获得维数更高的汉克尔矩阵H，因而子空间重建算法具有更好的性能。但是矩阵H维数增加会导致子空间重建算法复杂度增加，必须在重建性能和复杂度之间进行折中。

在没有噪声时，可以将汉克尔矩阵H分解为：

可以发现，矩阵R和S是移位不变矩阵。

当汉克尔矩阵H受噪声影响时，可以采用奇异值分解方法将H分解为：

求解范德蒙德线性方程组式(26)，得到UWB信号的幅度di。

分别求解式(24)和式(25)得到冲激串信号x(t)的时移ti和幅度di，然后根据式(2)完成UWB信号的重建。

3 仿真结果与讨论

本节通过仿真验证带通采样和子空间重建算法的有效性。仿真所采用UWB高斯单脉冲信号的宽度Td为0.5 ns，带宽为2.3 GHz，按照传统的香农采样定理，需要设计采样率为2倍信号带宽(=4.6 GHz)的ADC，这样高采样率的ADC是无法大规模低成本设计实现的。

设在UWB信号的一个帧中共有10个高斯单脉冲，脉冲重复周期Tf为50 ns，根据式(6)计算得到UWB脉冲信号的新息率为40 MHz，按照本文所提出的带通采样和子空间重建算法，以不同的采样率进行采样和重建，得到的归一化根均方重建误差如图2所示。图中未作任何标记的曲线为零化滤波重建方法的误差性能[8-11]；通过适当提高采样率，以2倍信号新息率(80 MHz)采样时，重建误差如图2中标记为“+”的曲线所示，其性能优于零化滤波重建算法，但其在低信噪比条件下重建误差仍然较高；以4倍信号新息率(160 MHz)采样时，子空间重建算法性能改善明显，在低信噪比条件下可获得较好的重建结果；继续提高采样率，以8倍信号新息率(320 MHz)采样时，重建误差仅比4倍信号新息率采样时的重建结果改善1～2 dB，而随着采样率提高，子空间重建算法复杂度增加，因此，以4倍信号新息率进行采样，能够以较低的复杂度获得良好的重建结果。

采用子空间算法重建UWB信号的结果如图3所示。图3a中绘出了3个原始高斯单脉冲信号，以及这些脉冲受噪声(信噪比10 dB)影响时的信号波形；使用本文所提出的子空间重建算法，采样速率为4倍信号新息率(160 MHz)，对UWB信号进行采样和重建，重建结果如图3b中虚线所示，可以看出，在信噪比为10 dB时，子空间算法可以准确地重建原始UWB信号。

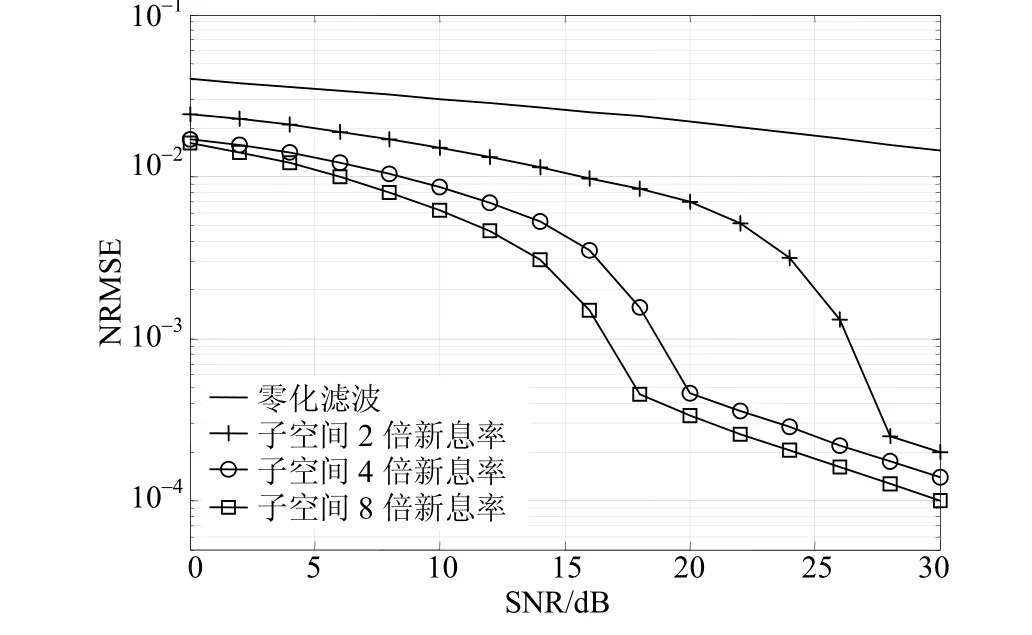
图2 时移估计归一化根均方重建误差

图3 UWB高斯单脉冲信号波形重建结果

4 结 论

本文对非带限信号的低通采样和零化滤波重建算法进行改造，提出了UWB脉冲信号的一种带通采样结构，并由此给出了一种子空间重建算法，通过适当提高采样率，以2倍、4倍或者8倍信号新息率进行采样，可以获得较现有零化滤波重建算法更好的重建性能。以8倍信号新息率进行采样时，本文算法所要求的采样率低于传统的香农采样定理1个数量级。分析和仿真结果表明，本文算法所要求的采样率低于传统香农采样定理；在低信噪比的情况下，本文算法的性能优于现有的零化滤波重建算法。

参 考 文 献

[1]WIN M Z, SCHOLTZ R A. Ultra-wide bandwidth time-hopping spread-spectrum impulse radio for wireless multiple-access communications[J]. IEEE Trans on Commun, 2000, 48(4): 679-691.

[2]CHEOLHEE P, RAPPAPORT T S. Short-range wireless communications for next-Generation networks: UWB, 60 GHz millimeter-wave WPAN, and ZigBee[J]. IEEE Wireless Commun, 2007, 14(4): 70-78.

[3]CHOI J D, STARK W E. Performance of ultra-wideband communications with suboptimal receivers in multipath channels[J]. IEEE J Sel Areas Commun, 2002, 20(9):1754-1766.

[4]CASSIOLI D, WIN M Z, VATALARO F, et al. Low complexity rake receivers in ultra-wideband channels[J].IEEE Trans on Wireless Commun, 2007, 6(4): 1265-1275.

[5]岳光荣, 李少谦. 超宽带冲激无线电性能比较[J]. 电子科技大学学报, 2003, 32(5): 477-480.YUE G R, LI S Q. Performance comparison of Ultra wideband impulse radio[J]. Journal of University of Electronic Science and Technology of China, 2003, 32(5):477-480.

[6]WALDEN R H. Analog-to-digital converter survey and analysis[J]. IEEE J Sel Areas Commun, 1999, 17(4):539-550.

[7]LE B, RONDEAU T W, REED J H,et al. Analog-to-digital converters[J]. IEEE Sig Proc Mag, 2005, 22(6): 69-77.

[8]VETTERLI M, MARZILIANO P, BLU T. Sampling signals with finite rate of innovation[J]. IEEE Trans on Sig Proc,2002, 20(6): 1417-1428.

[9]BLU T, DRAGOTTI P L, VETTERLI M, et al. Sparse sampling of signal innovations[J]. IEEE Signal Processing Magazine, 2008, 25(2): 31-40.

[10]KUSUMA J, RIDOLFI A, VETTERLI M. Sampling of communication systems with bandwidth expansion[C]//The 2002 IEEE International Conference on Communications. New York: IEEE, 2002, 3: 1601-1605.

[11]KUSUMA J, MARAVIC I, VETTERLI M. Sampling with finite rate of innovation: channel and timing estimation for UWB and GPS[C]//The 2002 IEEE International Conference on Communications. Anchorage, AK, USA:IEEE, 2003, 5: 3540-3544.

[12]HAYES M H. Statistical digital signal processing and modeling[M]. New York: John Wiley and Sons, 1996.

[13]张贤达. 现代信号处理[M]. 北京: 清华大学出版社,2002.ZHANG X D. Modern signal processing[M]. Beijing:Tsinghua University Press, 2002.

编 辑 张 俊

Subspace Reconstruction Method of UWB Signals Based on Sub-Sampling

YANG Feng1, HU Jian-hao2, and LI Shao-qian2

(1. Science and Tecknology on Electron Information Control Laboratory Chengdu 610036;2. National Key Laboratory of Science and Technology on Communications, University of Electronic Science and Technology of China Chengdu 611731)

In this paper, bandpass sampling and subspace reconstruction methods of ultra-wideband (UWB)signals are proposed, which can greatly reduce the sampling rate in UWB communications. The UWB signals are passed through a bandpass filter and sampled at several times of the innovation rate. Then the amplitudes and time shifts of UWB signals can be obtained by subspace reconstruction method. Analysis and simulation results show that the subspace method can precisely reconstruct the UWB signals at a sampling rate which is much lower than Nyquist rate.

bandpass sampling; innovation rate; subspace reconstruction; ultra-wideband

[8-11]提出了非带限信号的一种低通采样和零化滤波重建算法，对非带限信号按照信号新息率进行采样和重建，该方法在没有噪声影响的情况下可以准确地重建原始非带限信号，但其在噪声影响下会出现病态方程组，无法求解得到非带限信号的幅度和时移信息，算法抗噪声性能较差。

TN92

A

10.3969/j.issn.1001-0548.2010.06.008

2009- 05- 19;

2009- 09- 21

国家973计划(2007CB310604)

杨 峰(1978- )，男，博士，主要从事超宽带无线通信和移动通信技术方面的研究.

超宽带(UWB)无线通信技术因其具有数据传输率高、抗多径干扰能力强、定位精确和成本低廉等优点，在短距离高速无线通信、测距与定位、遥感以及汽车雷达等领域应用广泛[1-2]。脉冲超宽带(IR-UWB)通信系统使用纳秒甚至皮秒级宽度的脉冲信号传输信息，具有较强的多径分辨能力，通过使用RAKE接收机分集合并可以捕获尽可能多的多径能量，改善接收机性能[3-5]。但是设计RAKE接收机需要进行精确的信道参数估计，这就要求对UWB信号进行数字化采样，由于UWB脉冲占用非常大的带宽(≥500 MHz)，按照香农采样定理，需要设计采样率为几个吉赫兹的模数变换器(ADC)，将导致系统复杂度增加，成本上升，背离UWB系统设计的初衷。文献[6-7]的研究结果表明，限于半导体集成电路的工艺水平，目前已经商用的ADC最高采样率为1 GHz，不能满足UWB信号数字化采样的需求。虽然通过模拟方法可以降低ADC的采样率，但是模拟方法与数字信号处理算法相比，检测性能较差，信号处理灵活度较低。