密实和松散颗粒材料等吸力三轴剪切试验离散元数值模拟

蒋明镜，胡海军

(1. 同济大学 地下建筑与工程系，上海，200092；2. 同济大学 岩土及地下工程教育部重点实验室，上海，200092)

密实和松散颗粒材料等吸力三轴剪切试验离散元数值模拟

蒋明镜1,2，胡海军1,2

(1. 同济大学 地下建筑与工程系，上海，200092；2. 同济大学 岩土及地下工程教育部重点实验室，上海，200092)

从宏微观角度应用离散元研究吸力对密实和松散颗粒材料强度的影响。应用分层欠压法生成固定孔隙比的密实和松散长方体试样(长：宽：高=1：1：2)，在不同围压下固结，基于作者提出的相似理论，将吸力接触模型植入PFC3D中，计算吸力引起的颗粒间作用力。在等围压和等吸力下，对长方体试样进行三轴剪切试验，测得在剪切过程中轴向应力、轴向应变等宏观量和平均配位数、接触组构等微观量。研究结果表明：吸力能提高土的抗剪强度，提高试样的平均配位数；随着竖向应力增大，颗粒间接触主方向向竖直方向偏转；在相同吸力下，围压越大，接触点数越多，由吸力引起的抗剪强度越大。

非饱和土；离散元；吸力；抗剪强度；组构；配位数

路堤、堤坝、高于地下水的地表土等均是非饱和土，在涉及这类土的边坡稳定性计算分析时，均需要确定其抗剪强度。Bishop等[1−2]分别提出了非饱和土的抗剪强度f表达式：

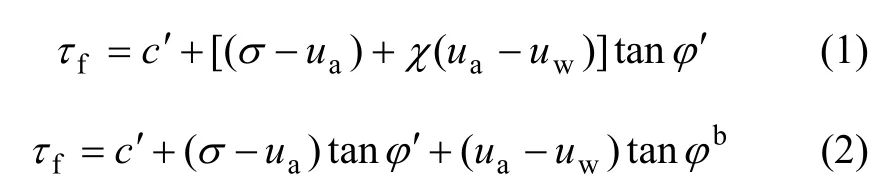
式中：(σ−ua)为净应力；(ua−uw)为基质吸力；c′为有效内凝聚力； ′为有效内摩擦角；χ为饱和度的函数，在0～1之间变化，为非常量；ϕb为随基质吸力而强度增加的内摩擦角，为非常量，随着饱和度或基质吸力而变化。离散元法[3]已经成功应用于砂土剪切试验[4−5]、结构性土压缩试验[6]、静力触探[7]和管涌现象[8]等分析中，用来从微观角度解释宏观现象。有研究表明：非饱和土强度随着吸力呈非线性增长且强度与级配密切相关，如Jiang等[9]应用二维离散元法研究了非饱和土的抗剪强度并提出了2个能够考虑大吸力范围和颗粒级配影响的抗剪强度函数。在此基础上，本文作者应用三维离散元法，将土颗粒等效为刚性球，允许刚性球之间有重叠以考虑实际颗粒弹性变形，将毛细水作用考虑入颗粒间作用力，从宏微观角度对等吸力下非饱和密实和松散颗粒材料进行三轴剪切试验分析。

1 毛细水作用在离散元分析中的实现

1.1 颗粒接触处毛细水引起的粒间作用力理论公式

为了简化，假设试样中的含水量仅由毛细水组成，并且忽略接触角。它的弯液面的形状如图 1(a)所示。毛细水引起的粒间作用力如图 1(b)所示。尽管Fisher等[9−11]指出表面张力对颗粒间作用力有贡献，但沿周长分布的表面张力在计算颗粒间作用力时常被忽略。根据图1(b)所示含毛细水颗粒间作用力，由力的平衡原理可得毛细水引起的颗粒间作用力FI：

式中：T为孔隙水的表面张力，15 ℃时为0.073 5 N/m。R1和R2可以用下式表示：

式中：r为颗粒半径；θ为持水角。吸力可以表示为：

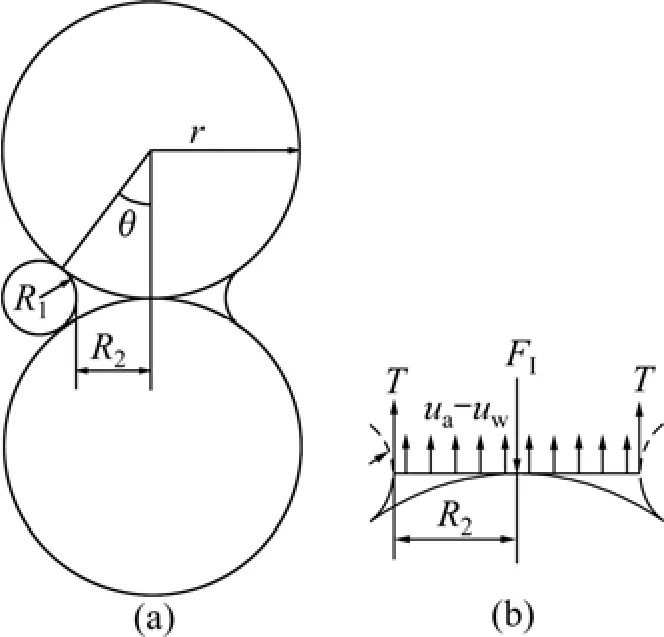
图1 毛细水模型示意图Fig.1 Schematic representation of capillary water model

将式(4a)，(4b)和(5)代入式(3)，可得：

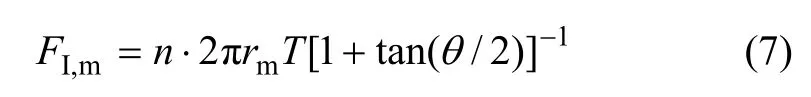
由式(4)，(5)和(7)可得到吸力和颗粒间作用力的关系。以2个等直径球体(半径为3.90 μm)为例，计算中模型颗粒半径为3.90 μm，n=1 000，由式(4)和(5)得到由吸力表示的θ，再代入式(7)可得吸力与颗粒间作用力的关系，如图2所示。原型颗粒间作用力为图2所示颗粒间作用力除以 106。从应力概念上，原型和模型是相等的。

从图2可以看出：随着吸力增加，粒间作用力呈非线性增加，假定颗粒间摩擦因数不随吸力变化而变化，在剪切过程中，吸力引起的抗剪强度为其引起的粒间作用力与摩擦因数的乘积，则毛细水引起的抗剪强度并非随着吸力线性增加，反映在式(1)和式(2)，χ和bϕ并非常数。这从微观解释了抗剪强度宏观表达式中吸力项参数并非常量。

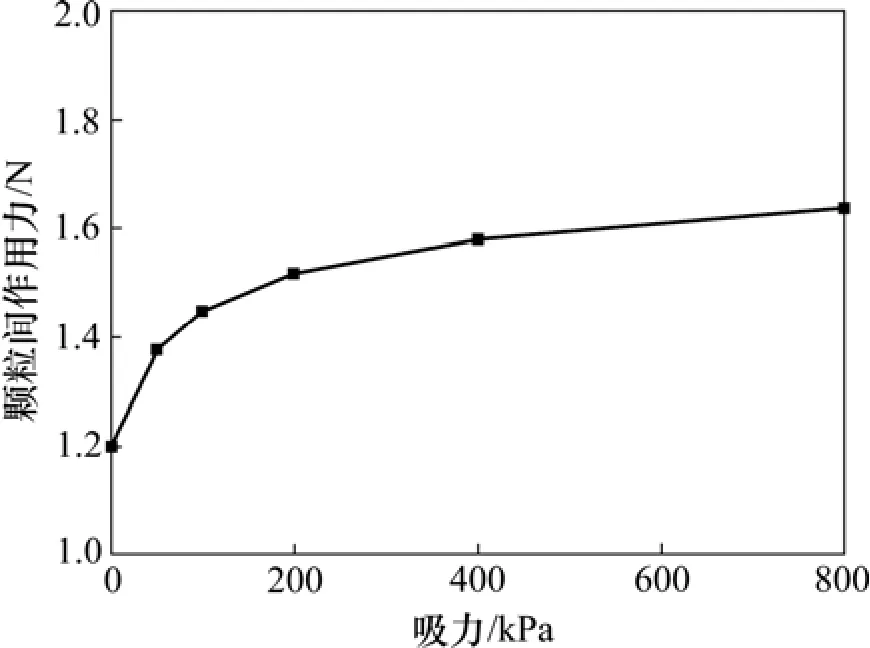
图2 颗粒间作用力与吸力的关系Fig.2 Relationship between interparticle force and suction

当吸力为 0时，持水角为 53.13°，小于 60°。不同排列形式下最大持水角如图3所示。2个等直径颗粒之间水膜持水角最大可为60°，证明持水角为53.13°水膜形式是存在的，此时颗粒间作用力不为 0，这表明当水压力和气压力相等时，颗粒间作用力仍然存在，是由水膜的表面张力引起。另外，对于砂土而言，由湿润状态变为干燥状态，对常规大吸力情况下即可变为干砂，其粒间作用力应为 0，即颗粒间作用力随着吸力变化存在1个峰值，而在Fisher公式中没有得到反映；对于粉土和黏土由湿润状态变为干燥状态需要很大的吸力，因此，在常规吸力下，颗粒间作用力随着吸力增加而增加是符合粉土和黏土特性的。尽管有以上问题存在，本文仍以Fisher的公式计算。要更精确地考虑范德华力、电子力、化学胶结力等颗粒间作用力的公式，还有待进一步研究。

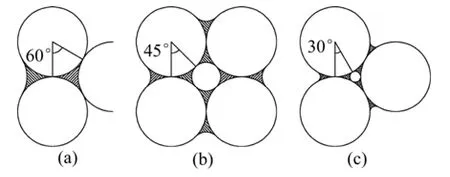
图3 不同排列形式下最大持水角Fig.3 Maximum water-retention angles under different arrangement forms

1.2 离散元分析中的毛细水模型

分析中采用的毛细水模型见文献[9]，本文将该模型扩展至三维空间中。

图4 离散元分析中提出的毛细水接触模型[9]Fig.4 Simplistic contact model proposed for capillary water in DEM[9]

假设土体的每个颗粒都是1个刚性圆球，这些颗粒都有自己的质量m，惯性矩为Io。每个粒子的移动(转动)速度xi(iθ)由牛顿第二定律计算(i代表x，y和z方向)。xi(iθ)用于计算速度从而求得位移。对于半径为r的每个颗粒，运动中法向和切向接触力分别用Tn,m和Ts,m来表示，它们可以分解成接触力Ti,m和关于物体中心的力矩M。然后，将p个相接触的颗粒对其作用力求和：

式中：Tn为通过颗粒间的重叠部分求得的法向接触力，在压缩接触中为正值；Tcw(＞0)为毛细水的黏结力，等于通过式(6)计算得到的毛细水引起的粒间作用力。(Tn－Tcw)为荷载导致的法向接触力；Dn为法向阻尼力，当颗粒分离时，Tn＝0，Dn＝0，Tcw＝0；Ts为切向接触力；则Ds为切向阻尼力。若Ts增大到接触模型的抗剪强度峰值，则Ds＝0。抗剪强度峰值为：其中：tanμ为粒间摩擦因数。若2个颗粒分离，则Ts＝0，Ds＝0。由动力学公式可知：离散元分析中的阻尼和动摩擦是用来消耗能量的。

在离散元分析中，广义有效应力ij(GES)[9]用下式表示：

由吸力引起的广义有效应力[9](GESS)也可由式(12)表示，粒间作用力仅包括毛细水引起的力。

1.3 三轴剪切过程中毛细水作用的研究

对2个半径为r1和r2的不等径球体，采用等径球体处理：

当基质吸力较小时，则可能相邻毛细水相互接触，如图3(b)所示。当持水角大于45°时，则连成一气泡，如图3(c)所示，当持水角大于30°时，则连成一气泡。根据Fredlund的研究[9−12]，这种孔隙将迅速被水充满。由式(5)可得：颗粒直径越小，持水角 30°所对应的吸力越大。对本文中的试验，采用高吸力可避免相邻颗粒毛细水连通形成气泡而造成数值计算繁琐的问题。

在PFC3d中编制fish语句，每当有新的颗粒接触时，将新产生的接触模型变为毛细水模型。这一实现过程在计算机中实现，比实际试验要快得多。

2 毛细水接触模型合理性的验证

2.1 吸力作用下2个颗粒拉伸试验和剪切试验

图5所示为吸力作用下2个颗粒拉伸试验和剪切试验结果，球的直径为3×10−6m，吸力为100 kPa。应用相似理论，颗粒的直径为3×10−3m，n=1 000。由式(5)可得持水角θ=33.13°，从式(7)可得由毛细水引起的颗粒间作用力理论值为1.092 N。

图5 2个含水与不含水颗粒试验示意图Fig.5 Sketch for tests on two grains with or without water

将吸力模型植入PFC3d中，对2个接触球进行拉伸和剪切试验。表1给出了试验中的材料参数。拉伸试验步骤如下：第1步，让2个球稍微接触(1×10−10m)，然后，在接触处施加1个吸力黏结；第2步，释放2个球体达到平衡状态；第3步，固定左边球体，将右边球体以固定速度(1×10−6m/s)朝离开方向移动。剪切试验(b)和(c)(见图 5)试验步骤如下：第 1和第 2步与拉伸试验的相同；第3步，固定左边球，在右边球上施加1个恒定2 N的法向力，当2个球再次达到平衡时，将右边球以恒定速度沿接触点切线方向移动。对于剪切试验(d)，试验步骤如下：第1和第2步与拉伸试验的相同；第3步，固定左边球，将右边球以恒定速度沿接触点切线方向移动。注意上述试验过程中均不允许颗粒有转动。

图6给出了拉伸和剪切试验中不平衡力和相对位移的关系。如图 6(a)所示，毛细水能够抵抗 1.092的拉伸力，这与理论值相等。如图6(b)所示，毛细水能够提高抗剪强度。图5(b)中的剪切强度由2个部分组成：一个是外力引起的剪切强度，另一个是毛细水引起的剪切强度，即：1.546 N(抗剪强度)=1.092 N(毛细水引起的颗粒间作用力)×0.5(摩擦因数)+2 N(外荷载)×0.5(摩擦因数)。

2.2 吸力作用下正方性规则排布试样水力试验

试样由8 000个半径为3.90 μm的球按规则正方形排布而成，选取的半径为3.90 μm和后面试验试样d50相等。分析中采用的颗粒半径为3.90 μm，n=1 000，起始时每相邻球之间有微小的接触(1×10−10m)，然后，在接触处施加吸力黏结；接着，所有球体达到平衡状态，用应力球测试广义应力。

表1 离散元分析中的材料参数Table 1 Material parameters used in DEM analyse

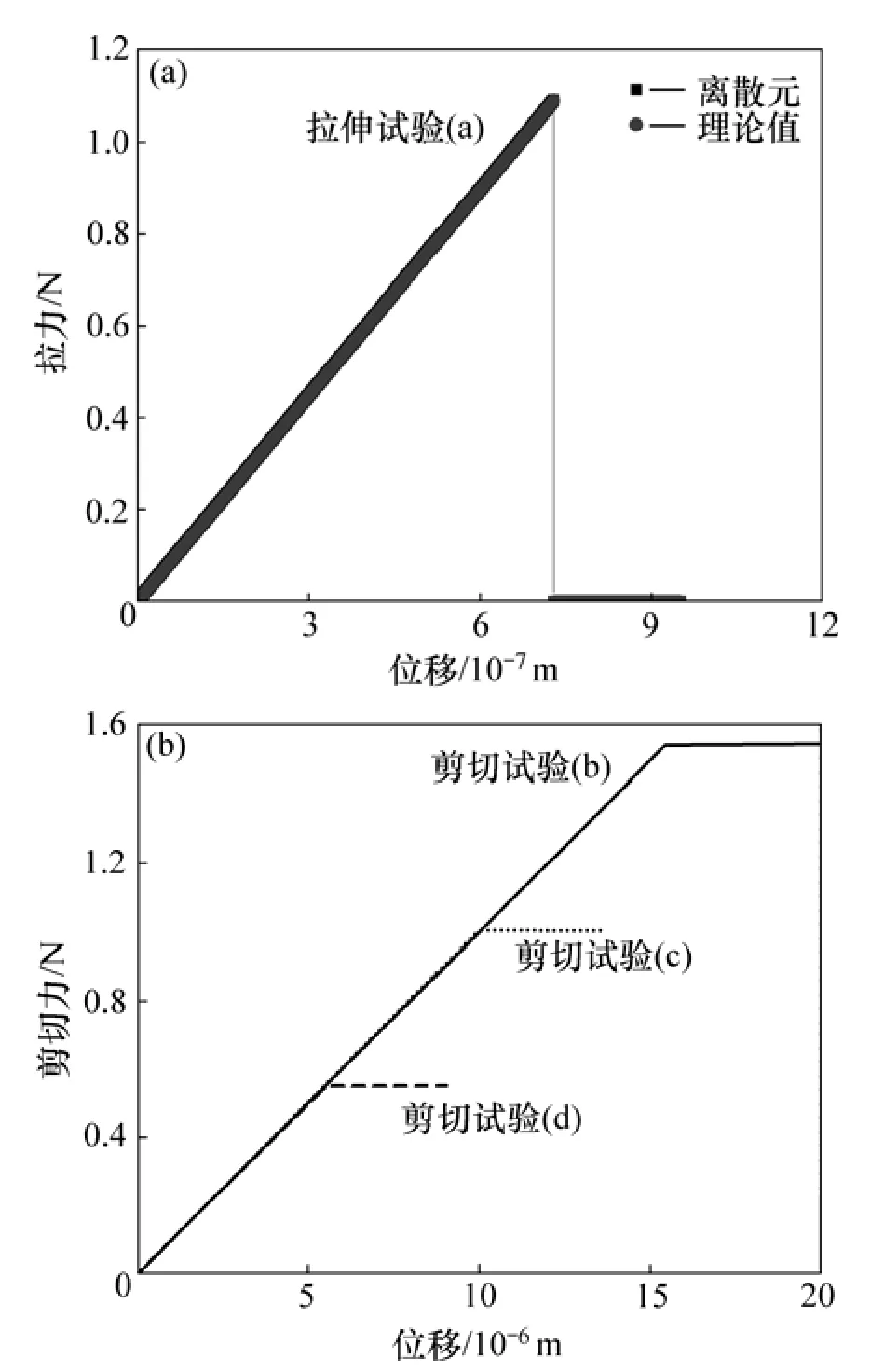
图6 拉伸试验和剪切试验结果Fig.6 Results of tension test and shear test

理论上，由于吸力引起的广义有效应力eq可用下式表示：

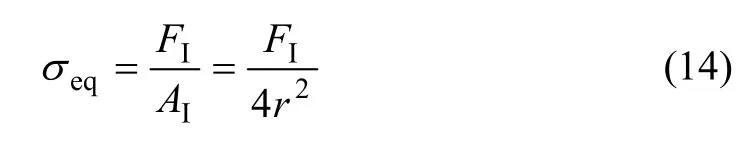
式中：AI为FI所作用的面积。当弯液面接触时，这个简单立方体中所有接触点处的临界角为 45°。当持水角θ＞θc时，Sr为100%。根据前者提到的渗透过程，所有孔隙都同样充满水。当θ＜θc时，在简单立方体中，考虑到每个球都与其他球有4个接触点，Sr的理论计算公式如下；

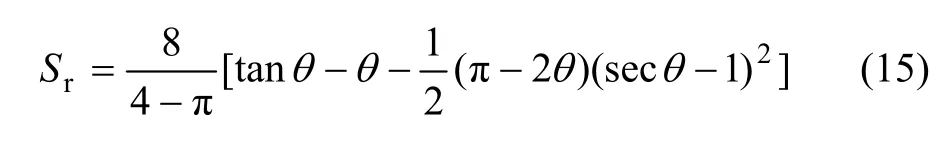
图7所示为吸力和GESS的关系，还有由理论方法推导得到的土水特征曲线。由图7可知：DEM结果与理论值完全一致，证明了相似理论的正确性与接触模型的正确性和合理性。当吸力减小、Sr增大时，GESS减小。当吸力低于13.327 kPa时，GESS突然减小至0 kPa，而饱和度增至100%。

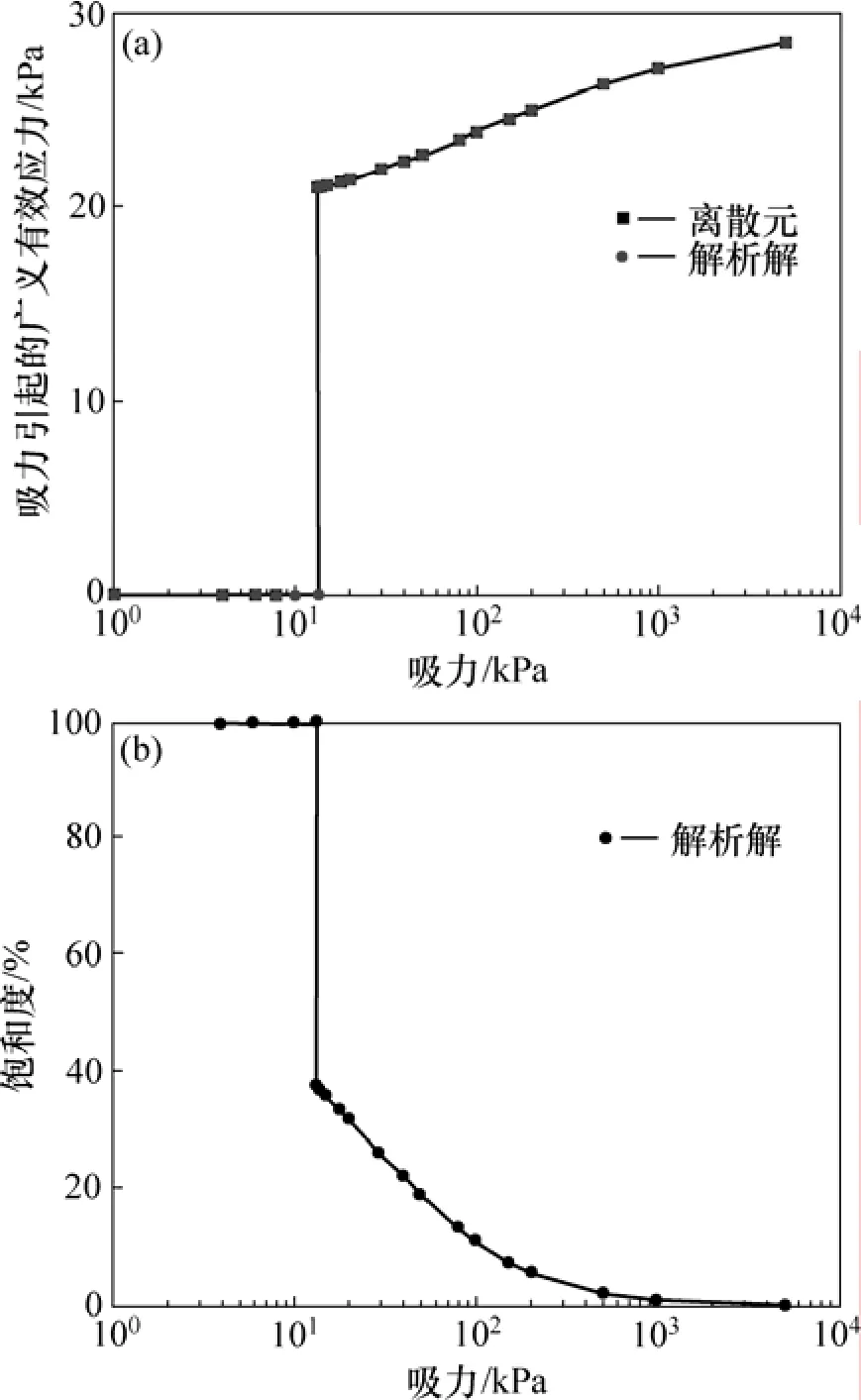
图7 不同吸力作用下试样的广义应力、饱和度与吸力的关系Fig.7 Relations of suctions with generalized effective stress and degree of saturation

3 密实和松散颗粒材料等吸力三轴剪切试验离散元数值模拟

3.1 试样颗粒级配

本文研究原型试样的颗粒级配如图8所示。按此级配属于粉粒土。试样最大颗粒直径为10.50 μm，最小直径为 6.60 μm，d50=7.75 μm。不均匀系数为Cu=d60/d10=1.2。密实颗粒试样孔隙比为0.5，松散颗粒试样孔隙比为0.82。试样中总颗粒数目为10 000。离散元分析中采用相似系数为n=1 000，即颗粒放大1 000倍。各直径的颗粒数目由Jiang等[13]提出的公式计算：

式中：Nj为j颗粒的颗粒数；wj为j颗粒(半径为rj)的质量分数；n为颗粒直径种类数；N为总颗粒数，此处等于10 000。

图8 原型试样的颗粒分布Fig.8 Grain-size distribution of prototype

3.2 试样制备

试样首先应用由 Jiang等[13]提出的分层欠压法生成，共分5层。分层欠压的目的是克服等厚度分层制样造成下层密实上层松散的问题。该法在分层压缩试样时，第1到第n层平均孔隙比比目标孔隙比e大，直到压缩到最后一层等于目标孔隙比e。密实试样采用的欠压法则为：=0.528,=0.527,=0.521,=0.512,=0.500；松散试样采用的欠压法则为：=0.930,=0.914,=0.895,=0.870,=0.820。 颗粒法向刚度为 1.5×106N/m，切向刚度为1.0×106N/m。墙的法向刚度为1.5×105N/m。密实试样生成时，压缩过程中球和墙的摩擦因数设置为 0；松散试样生成时，压缩过程中球的摩擦因数设置为1，墙的摩擦因素设置为0。密实试样在50 kPa下固结，这一过程之后将球之间的摩擦因数设置为0.5，然后试样分别在100和200 kPa下固结；松散颗粒材料在成样后，将球之间的摩擦因数改为0.5，然后，侧墙固定，在竖直方向施加12.5 kPa的应力，使试样中的颗粒充分接触，在50，100和200 kPa下固结。对非饱和状态，不同固结压力下的试样施加100和200 kPa的吸力作用。对于所用试样，颗粒最小直径为 6.60 μm。最密实状态排布如图3(c)所示，最大持水角为30°对应的吸力为91.276 kPa。对于本次试验，吸力为100和200 kPa，对不同粒径持水角均小于30°，因此，不会出现弯液面连通形成气泡的情况。

3.3 剪切试验离散元分析

对无吸力试样，吸力为100和200 kPa的试样分别在各恒定围压(50，100和200 kPa)下，按恒定1%/s应变速率(该速率经过对比调试得到，更小的速率虽然更加逼近准静态过程，但会消耗更多的计算机时间，用该速率得到的强度与更小应变速率得到的强度相差不大)进行竖向压缩，试验过程中保证吸力恒定。墙和颗粒间的摩擦因数设置为 0，以消除颗粒与墙的边界效应。在剪切试验中，记录轴向应力、轴向应变、侧向应变等宏观参数和平均配位数、接触组构等微观参数以研究宏微观变量之间的关系。

4 吸力对密实和松散颗粒材料剪切试验宏微观参数变化的影响

4.1 应力与应变关系及强度特性

图9所示为无吸力密实试样剪切过程的应力与应变的关系。由图9可见：该试样呈应变软化特性，反映了密实土的特性。图10所示为恒吸力为100 kPa时密实试样剪切过程的应力与应变关系。从图9和图10可以看出：由于吸力的存在，使得试样软化更明显。

图9 密实干样在不同围压下应力与应变的关系Fig.9 Relationships between deviatoric stress (σ1−σ3) and axial strain of dry dense samples under different confining pressures

图10 密实试样在吸力为100 kPa时不同围压下应力与应变的关系Fig.10 Relationships between deviatoric stress (σ1−σ3) and axial strain of dense samples under different confining pressures with Su=100 kPa

图 11所示为无吸力松散试样剪切过程的应力与应变的关系。该试样呈应变硬化特性，反映了松散土的特性。图12所示为恒吸力100 kPa下松散试样剪切过程的应力与应变的关系。从图11和12可以看出：由于吸力的存在，使得试样由应变硬化向应变软化发展。

表2所示为无吸力、吸力分别为100和200 kPa时密实和松散试样剪切过程最大剪应力。由表2可见：吸力可提高剪切过程中的抗剪强度。

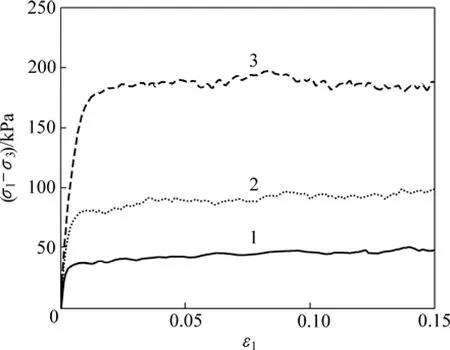
图11 松散干样在无吸力时不同围压下应力与应变的关系Fig.11 Relationships between deviatoric stress (σ1−σ3) and axial strain of dry loose samples under different confining pressures without suction

图12 松散试样在吸力为100 kPa时不同围压下应力与应变的关系Fig.12 Relationships between deviatoric stress (σ1−σ3) and axial strain of loose samples under different confining pressures with Su=100 kPa

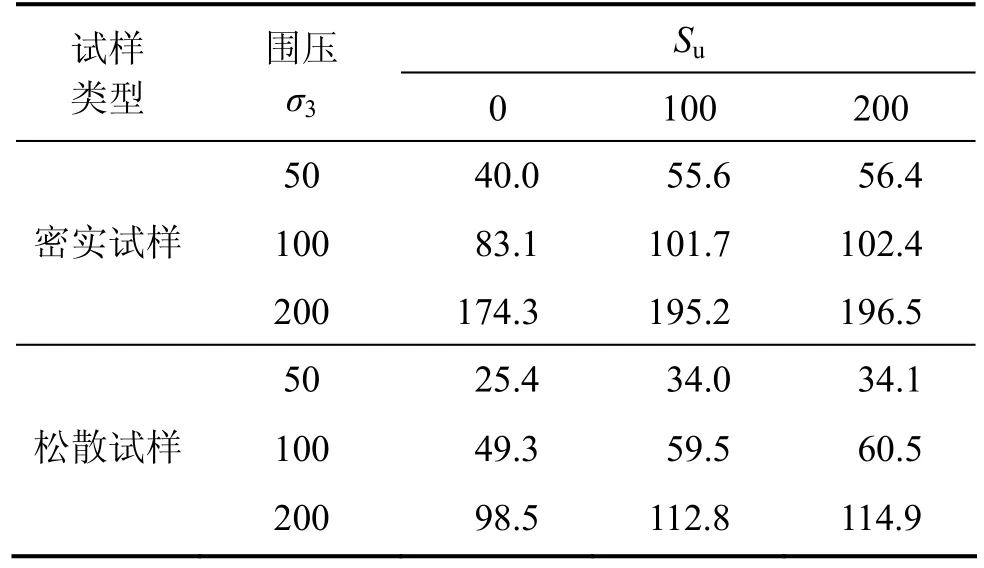
表2 试样三轴剪切试验中最大剪应力Table 2 Maximum shear stress (σ1−σ3)/2 during shearing kPa

表3所示为毛细水对剪切过程最大剪应力的提高值。结果表明：随着围压的提高，提高值增大，特别对于松散样，这种情况更为明显。这是因为在高围压下，有更多颗粒接触点即毛细水结合点，由吸力引起的抗剪强度越大。

4.2 接触组构

每个接触点有2个接触方向，使n和−n为单位接触方向矢量。如图11所示，可以用φ和θ定义n。

二阶接触组构张量定义如下[14]：

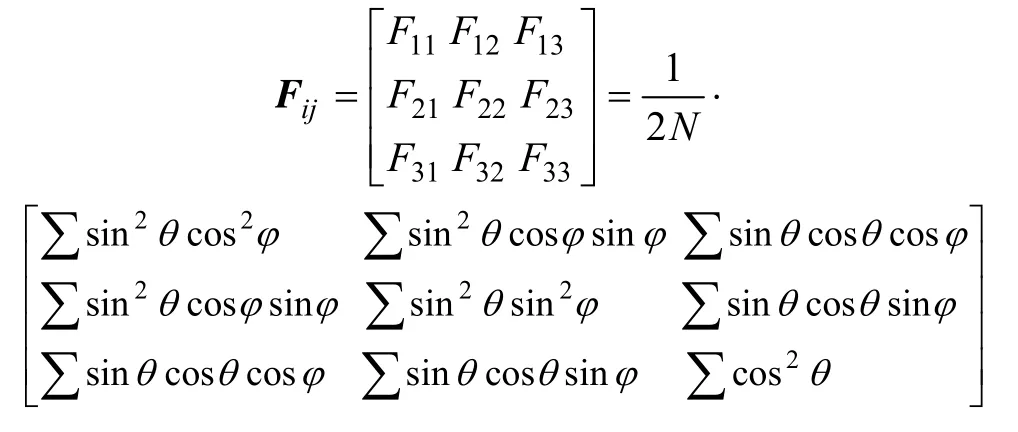
表3 由于毛细水引起的最大剪应力的提高值Table 3 Increase of maximum shear stress of unsaturated soil due to capillary water kPa

图13 n向量的表示Fig.13 Polar coordinates φ and θ to define n

当主对角线的F11，F22和F33相等时，代表接触方向在空间分布各向同性；某一值大，表示接触方向倾向于该方向分布。

表4列出了围压为200 kPa时密实样剪切过程中接触组构值变化。由表4可以看出：F33增大，表明接触方向向x3方向(竖直方向)偏转，说明在接触点向竖直方向偏转。另外，在有吸力和无吸力同一轴向应变下，接触组构值很接近，说明主要是外荷载对其组构产生影响，即吸力对试样的作用为近似各向同性。图14给出了围压为200 kPa时剪切前与破坏后接触方向在空间的密度分布。从图14可以看出：竖向应力的增加会使颗粒间接触方向朝向竖直方向偏转。

4.3 配位数

配位数定义如下：K＝2M/N(式中：M为颗粒与颗粒间的接触点个数；N为颗粒的个数)。K与强度密切相关。

图15所示为密实样平均配位数(K)在剪切过程中的变化。表明平均配位数随着轴向应变增加而减少，说明试样密实度降低，这与应变软化相对应。图15(a)和(b)表明：在给定吸力下，K随着固结应力增加而增加，说明随着固结压力的增加，密实度增加，这与传统土力学原理相符；在固定围压下，K随着吸力而增大，说明吸力的增加不仅会使由毛细水引起的颗粒间作用力增大，还有可能使试样在剪切过程中K增大。

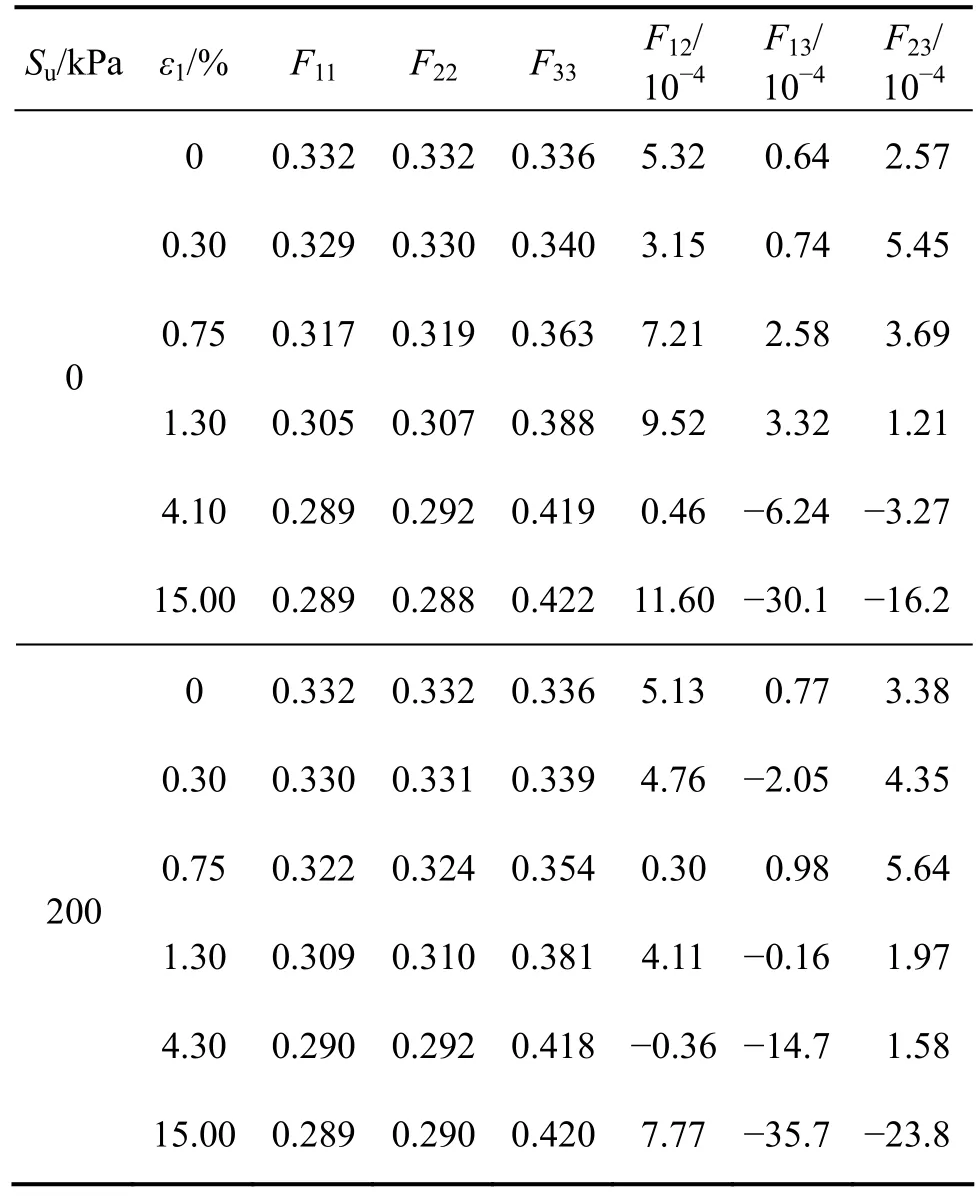
表4 围压为200 kPa时密实样在剪切过程中接触组构值变化Table 4 Contact fabric of dense sample during shear test under confining stress 200 kPa

图14 围压为200 kPa时密实样接触方向在空间上的密度分布Fig.14 Distributions of contact orientation density of dense samples in space under σ3=200 kPa

图16所示为松散样平均配位数(K)在剪切过程中的变化。由图16可知：平均配位数随着轴向应变增加先增加后保持稳定波动，说明试样密实度先增加，这与应变硬化相对应。对比图16(a)和(b)可知：随着吸力的增加，平均配位数增加。

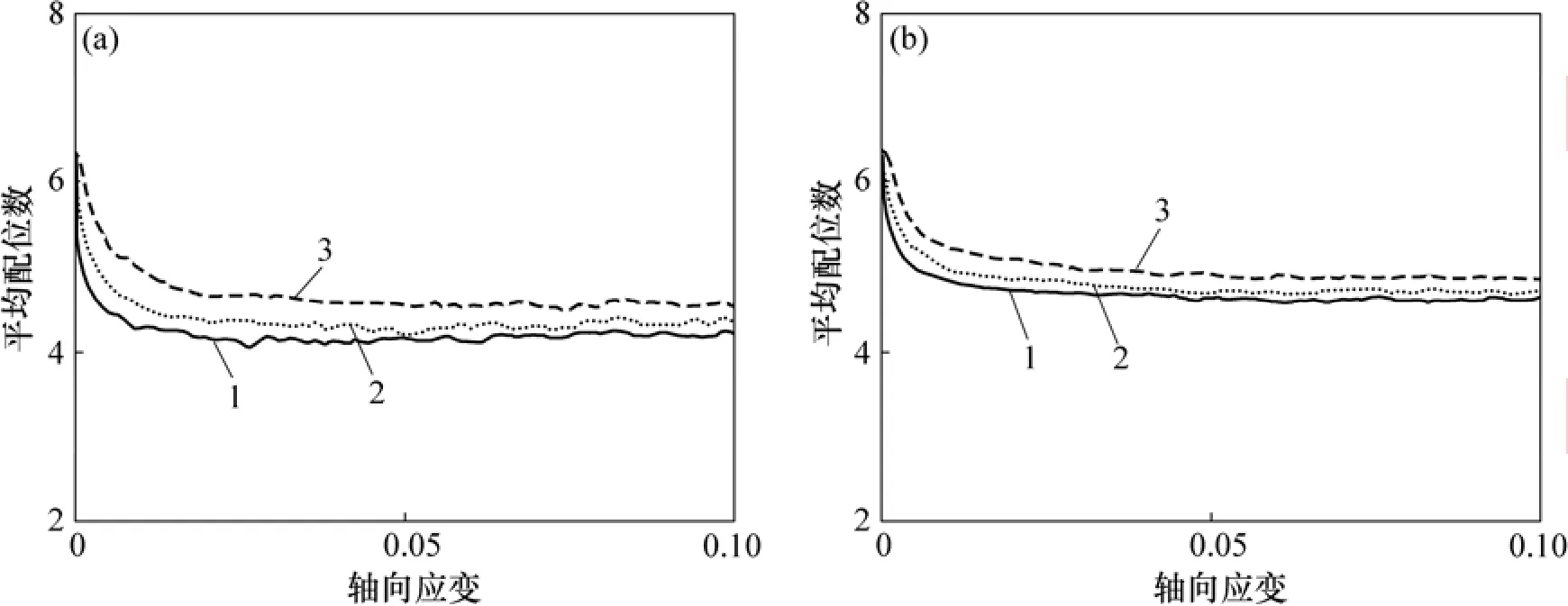
图15 密实样在不同围压下剪切过程中平均配位数与轴向应变的关系Fig.15 Relationships between average coordination number and axial strain of dense sample during shearing under different confining stresses

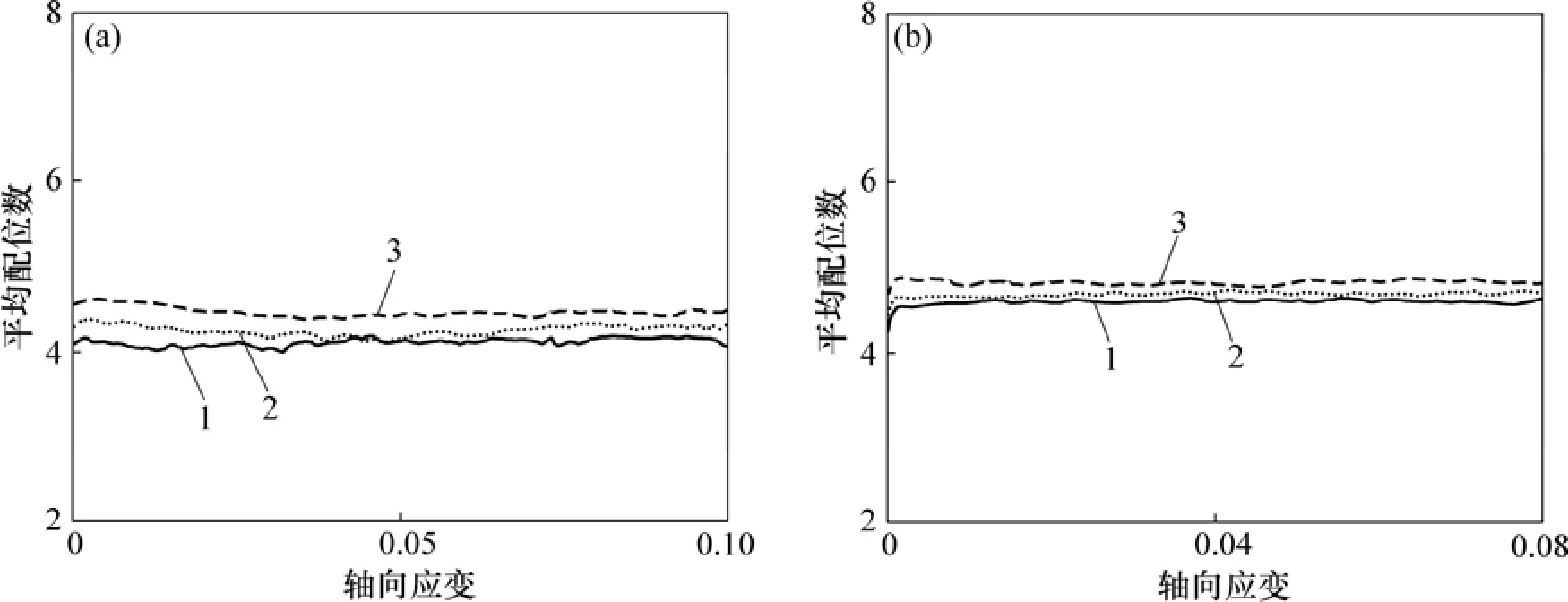
图16 松散样在不同围压下剪切过程中平均配位数与轴向应变的关系Fig.16 Relationships between average coordination number and axial strain of loose sample during shearing under different confining stresses

5 结论

(1) 非饱和土颗粒间抗剪强度由 2个部分组成：一部分是外荷载，另一部分是由吸力引起的颗粒间作用力，强度与颗粒间作用力成正比；吸力是通过增加颗粒间作用力来提高强度的，其颗粒间作用力并非随着吸力增加而呈线性增加。这从微观上解释了宏观表达式中吸力项强度并非随吸力增加线性增加。

(2) 密实和松散干颗粒材料在剪切过程中分别呈应变软化和应变硬化现象，这与传统土力学相符；本研究颗粒级配松散颗粒材料在吸力为100和200 kPa、围压为50，100和200 kPa条件下均呈应变软化，说明吸力可以改变应力−应变特性。

(3) 在剪切过程中，主要是外荷载引起接触组构变化，吸力影响很小，说明吸力的作用近似各向同性。

(4) 在相同吸力下，围压越大，接触点数目越多，毛细水对抗剪强度的贡献越大。

(5) 实际中的颗粒材料并非球形，颗粒之间存在咬合作用，下一步是要将考虑颗粒之间抗转动能力的模型引入三维离散元非饱和颗粒材料的分析。

[1] Bishop A W, Blight G E. Some aspects of effective stress in saturated and partly saturated soils[J]. Geotechnique, 1963, 13(3):177−197.

[2] Fredlund D G, Morgenstern N R, Widger R A. The shear strength of unsaturated soils[J]. Canadian Geotechnical Journal, 1978,15(3): 313−321.

[3] Cundall P A, Strack O D L. The distinct element method as a tool for research in granular media: Part Ⅰ[R]. Minnesota:University of Minnesota, 1978: 1−97.

[4] Thornton C. Numerical simulations of deviatoric shear deformation of granular media[J]. Geotechnique, 2000, 50(1):43−53.

[5] JIANG Ming-jing, ZHU He-hua, LI Xiu-mei. Strain localization analyses of idealised sands in biaxial tests by distinct element method[J]. Frontiers of Architecture and Civil Engineering in China, 2010, 4(2): 208−222.

[6] JIANG Ming-jing, Yu H S, Harris D. Bond rolling resistance and its effect on yielding of bonded granulates by DEM analyses[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(7): 723−761.

[7] JIANG Ming-jing, Yu H S, Harris D. Discrete element modeling of deep penetration in granular soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006,30(4): 335−361.

[8] 蒋明镜, 胡海军, Murakami A, 等. 管涌现象的离散元数值模拟[J]. 武汉大学学报: 工学版, 2008, 41(增刊): 19−24.

JIANG Ming-jing, HU Hai-jun, Murakami A, et al. Numerical analysis of piping by DEM[J]. Engineering Journal of Wuhan University, 2008, 41(S): 19−24.

[9] JIANG Ming-jing, Leroueil S, Konrad J M. Insight into shear strength functions of unsaturated granulates by DEM analyses[J].Computers and Geotechnics, 2004, 31(6): 473−489.

[10] Fisher R A. On the capillary forces in an ideal soil; correction of formulae given by W B Haines[J]. The Journal of Agricultural Science, 1926, 16(3): 492−505.

[11] Cho G C, Santamarina J C. Unsaturated particulate materials particle-level studies[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(1): 84−96.

[12] Fredlund D G. Density and compressibility characteristics of air-water mixtures[J]. Canadian Geotechnical Journal, 1976,13(4): 386−396.

[13] JIANG Ming-jing, Konrad J M, Leroueil S. An efficient technique for generating homogeneous specimens for DEM studies[J]. Computers and Geotechnics, 2003, 30(5): 579−597.

[14] Oda M, Iwashita K. Mechanics of granular materials[M].Netherlands: A A Balkema, 1999: 1−80.

[15] JIANG Ming-jing, Yu H S, Harris D. A novel discrete model for granular material incorporating rolling resistance[J]. Computers and Geotechnics, 2005, 32 (5): 340−357.

(编辑 陈爱华)

Numerical simulation of triaxial shear test of dense and loose granulates under constant suction by discrete element method

JIANG Ming-jing1,2，HU Hai-jun1,2

(1. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China;2. Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education,Tongji University, Shanghai 200092, China)

The effect of suction on the strength of unsaturated dense and loose granulates from macro and micro view was investigated by three-dimensional discrete element method (DEM). The samples were generated by multi-layer with undercompaction method and then consolidated under different confining pressures. Based on the similarity theorem, the suction contact model was implemented into a three-dimensional DEM software to calculate interparticle force due to capillary water. Triaxial shear tests were performed on the cubic unsaturated samples to study shear strength of samples.Macroscopic variables (e.g., axial stress, axial strain) and microscopic variables (e.g., average coordination number,contact fabric) during shear test under different consolidation stresses with different suctions were measured. The results show that suction leads to higher shear strength and average coordination number of granulates than dry granulates. When the vertical load increases, the main contact orientation moves towards the vertical direction. Under the same suction, the numbers of contact points and shear resistance due to capillary water increase with the confining pressure.

unsaturated soil; discrete element method; suction; shear strength; fabric; coordination number

TU441.32

A

1672−7207(2010)06−2350−10

2009−10−15；

2009−12−21

国家自然科学基金资助项目(10972158)；国家杰出青年基金资助项目(51025932)

蒋明镜(1965−)，男，江苏如皋人，教授，博士生导师，从事天然结构性黏土、砂土、太空土、深海能源土、非饱和土的宏观和微观试验、本构模型和数值分析研究以及土体逐渐破坏分析研究；电话：13761404246；E-mail: mingjing.jiang@tongji.edu.cn