基于BP网络的注塑成型模具硬态高速铣削力研究

王凌云，黄红辉

(上海工程技术大学 制造工程系，上海，200437)

基于BP网络的注塑成型模具硬态高速铣削力研究

王凌云，黄红辉

(上海工程技术大学 制造工程系，上海，200437)

用AlTiN 涂层硬质合金立铣刀对4Cr5MoSiV1钢注塑成型模具进行硬态高速铣削，研究切削加工参数对切削力的影响；通过多因素法进行正交试验，利用改进的BP神经网络建立切削力的神经网络模型并对工艺参数进行优化，将网络预测结果与现场加工实践数据进行对比。研究结果表明：人工神经网络能准确地预测铣削力，模型具有较强的泛化能力和自适应能力；在高转速、小切深、合适的进给速度以及微量切削液状态下铣削力较小，为优化模具硬态铣削的切削参数并对其实际生产应用提供了较好的依据。

模具硬态铣削；BP神经网络；铣削力模型；参数优化

在高速硬切削条件下，切削力直接影响切削热的产生，并进一步影响刀具磨损和破损、刀具寿命及已加工表面的质量。在生产中，切削力又是计算切削功率，合理选择和使用机床、刀具和夹具的必要依据。铣削力建模常用的方法有分析方法、试验方法、机械方法和数值方法4种[1]，Takashi等[2−12]用多种不同形状的刀具及刀具−工件材质组合在不同切削条件下获得的试验数据研究铣削力，但较少考虑切削速度、轴向及径向切深、进给量等重要加工参数的综合影响[13]。人工神经网络(ANN)是由大量的、较简单的处理单元(或称神经元)广泛地互相连接而成的复杂网络系统，具有大规模并行分布存储和处理、自适应和自学习能力，特别适用于处理需要同时考虑许多因素和条件的、不精确和模糊的、非线性以及模式特征不明确的问题，近年来已广泛应用于许多工程领域。本文作者综合考虑切削用量、微量润滑油量等参数对铣削力的影响，利用改进的BP神经网络建立铣削力模型，研究模具高速硬切削切削力的规律，并将其运用于模具实际生产中。

1 试验

1.1 试验系统

试验材料为 4Cr5MoSiV1钢。机床为 MAKINO高速立式加工中心V33。采用牧野(日本)的高速主轴，转速为2.0×104r/min，快移速度为 20 m/min，采用轴心冷却，轴承内润滑方式，由高速回转发生的热位移抑制至最小限度，加工精度稳定。

在试验中，采用的刀具参数不变且加工系统处于稳定切削状态。刀具采用直径为8 mm的AlTiN涂层硬质合金立铣刀，螺旋角为30˚。

试件为一注塑件的模具型腔，该模具产品的尺寸较小，材料为 ABS，结构如图 1所示。型腔材料为4Cr5MoSiV1淬硬钢，硬度(HRC)为 55，采用潜伏式浇口进胶，定模型腔结构如图2所示。

图1 试件结构图Fig.1 Structure of mold product

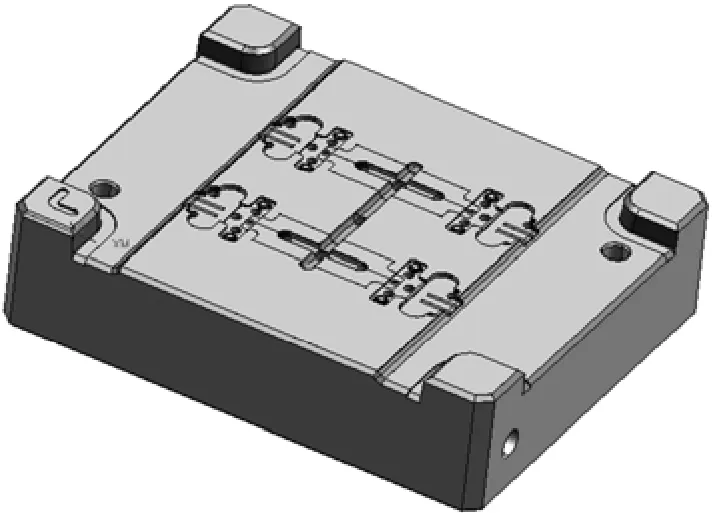
图2 模具型腔结构Fig.2 Structure of mold parts (cavity)

测试仪器为 Kistler9257A三向压电式动态测力仪，Kistler多通道电荷放大器以及相应的数据采集与处理系统。

1.2 试验方法

对定模模具零件进行高速硬态铣削(可以在淬火后一次性铣成)。采用多因素正交试验，选取现场加工参数，采用基于数值优化的Levenberg-Marquardt算法(简称LM算法)，利用改进的BP神经网络建立铣削力模型，研究模具高速硬切削切削力的规律。采用该算法不仅可以提高网络学习速度，还可以增加算法的可靠性，用于切削力预测的效果良好。

切削力F取3个切削分力平方和的平方根，切削分力的测量结果则是从测试软件上提取的动态切削力。

2 试验结果与分析

2.1 正交试验

按照L25(55)正交表共设计了5×5组试验用于训练神经网络，5个切削参数为：主轴转速n(r/min)、轴向切削深度ap(mm)、径向切削深度ae(mm)、进给速度vf(mm/s)和微量润滑液量Q(mL/h)。试验数据及切削力实测值如表1所示。表1中的切削参数是根据模具零件加工生产现场的高速精加工要求进行选取，以提高模具零件加工铣削力预报模型的精度。

2.2 铣削力的预测模型

图3所示为BP网络结构图。采用三层BP神经网络进行切削力的预测，其中：xi为输入层节点，分别表示转速n、轴向切深ap、径向切深ae、进给速度vf及润滑液量Q，yj为隐含层节点；zl为输出层节点，表示合力F。

输入层有5个节点，隐含层有11个节点，输出层有1个节点。上、下层之间各神经元实现全连接，即下层的每一单元与上层的每一单元都实现全连接，而每层各神经元之间无连接。网络按有教师示教的方式进行学习，当一对学习模式提供给网络后，神经元激活值从输入层经中间层向输出层传递，在输出层的各神经元获得网络的输入响应。之后，按减小希望输出与实际输出之间误差的方向，从输出层经各中间层逐层修正各连接权值，最后回到输入层。

隐含层输出为：

表1 铣削力模型训练样本Table 1 Model of training samples

图3 BP网络结构图Fig.3 BP neural network structure

其中：wji为输入层节点i与隐含层节点j之间的网络权值；j为隐含层的阈值；f为激励函数，采用Sigmoid型，即

输出层的输出为：

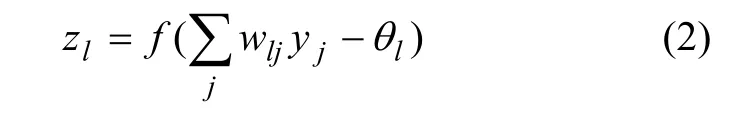
其中：wlj为隐含层节点j与输出节点之间网络权值；l为输出层的阈值。输出节点误差为：

其中：tl为目标输出。输入层节点误差δl为：

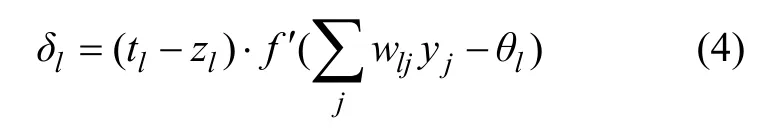
其中：f′表示对函数f求导。

隐含层节点误差jδ′为：

权值修正为：

其中：Δwlj和Δwji为网络权值变量的增量； 为反映训练速率的比例系数。

2.3 BP算法的改进

BP算法由于自身的原因不可避免地具有收敛速度慢和极易陷入局部极小值等缺陷，因此，通常需要对BP算法进行改进。对BP算法进行改进的方法比较多，本文作者采用LM算法改进BP算法。LM算法属于一种利用标准的数值优化技术的快速算法，其形式如下。

权值修正量：

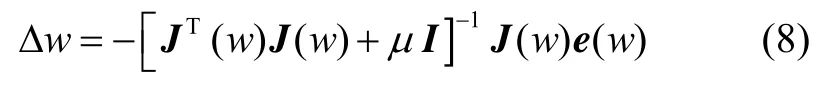
式中： ( ＞0)为比例系数；I为单位矩阵；J(w)为误差权值Jocobain矩阵；e为误差矢量。

从式(8)可知：如果 取值大，则LM算法接近梯度下降法。每迭代成功一步，则 减少，在接近误差目标时，则逐渐与高斯−牛顿法相似。由于 LM 算法利用了近似的二阶导数信息，因此，它的收敛速度比梯度下降法快。算法步骤如下。

步骤1设置初始权值w0为较小的随机非零值；

步骤 2给定输入/输出样本对，计算网络各层的输出；

步骤3计算网络的输出误差E；

步骤4计算各层误差l和δj′；

步骤5调整各层权值；

步骤6检查是否对所有样本完成1次轮训，未完成则返回步骤2；

步骤7检查网络总误差是否达到精度要求，若未达到，则返回步骤2。

对神经网络进行训练的过程实际上是一个函数逼近的过程，也就是对神经网络内部的神经元之间相互作用的连接权值不断修改的过程。取误差允许值ε=1×10−6，μ=0.1，隐含层结点数n=11，初始化网络权值向量 w0, 取上述 25组铣削试验数据作为训练网络的样本。

用 MATLAB工具箱实现以上过程，其程序代码的主要部分如下：

其中：t为输出层铣削力试验值的向量；p为输入层5个参数试验值的向量；F为铣削力的归一化处理值。

图4所示为网络训练次数与误差的关系。从图4可知：经过213次训练后，网络收敛至目标误差内。图5所示为神经网络铣削力预测曲线图。从图5可知：预测值与实测值拟合较好。

图4 网络训练次数与误差的关系Fig.4 Relationship between training times and error

图5 神经网络铣削力预测曲线图Fig.5 Neural network forecasting graphs of milling force

2.4 预测模型的应用

在一些注塑模具零件的加工中，用铣削力的预报模型得到的预测值与实测值进行比较得出：该模型的预测精度达到90.21%，表明所建立的模型具有较强的预测能力。

2.5 切削参数对铣削力的影响分析

在相对低的转速(切削速度)区域(1.05×104～1.45×104r/min)，当主轴转速增大时，各切削分力均不同程度地增大，而径向切深、轴向切深、进给速度及微量润滑液量增大，切削力增大，但增大的幅值不同，表明各参数对其影响程度不同；在相对高的转速1.65×104r/min下, 应变率强化作用得到较大加强，虽然热软化作用有一定的加强，但因应变率强化作用占主导地位，切屑剪切变形也开始局部化，再加上剪切角增大，使得切削力增大；在转速为1.85×104r/min时，随着转速(切削速度)的进一步增大，热软化作用占主导地位，切屑剪切变形更加局部化，切削力开始随切削速度的增大而减小。

切削速度对切削力的影响比较复杂。一方面，切削速度的提高导致剪切角增大，剪切力降低，随着切削温度的升高，摩擦因数明显减小，剪切力减小；另一方面，剪切角增大及切削速度本身的提高又会使切屑惯性力增大。但在精加工中，切深和每齿进给量都较小，切屑的质量小，虽然惯性力随切削速度提高而增大，但其增加幅度比剪切力减小幅度小得多，故切削速度的提高最终导致切削力的降低。

2.6 切削参数优化选择

用改进的 BP神经网络对铣削力进行预测，用MATLAB编程对预测的数据进行排序，按照如图6所示的程序算法框图求取铣削力F的最小值Fmin，在试验数据区间段，当主轴转速为1.05×104r/min、轴向切削深度为0.06mm、径向切削深度为0.04 mm、进给速度为1.6 m/s和微量润滑液量为80 mL/h时，切削力最小为82.0 N；而在主轴转速为1.85×104r/min、轴向切削深度为0.09 mm、径向切削深度为0.04 mm、进给速度为2.8 m/s和微量润滑液量为140 mL/h时，切削力仅有较小的增加。结合表面粗糙度研究结果，综合考虑切削力及加工质量[14]，采用高转速、小切深、合适的进给速度以及微量润滑液状态下时，注塑成型模具进行硬态高速铣削效果好。

图6 求取Fmin的算法框图Fig.6 Diagram of algorithm of solving Fmin

2.7 其他参数分析

采用逆铣容易获得更小的壁直线度公差和 90°角公差。当不同轴向走刀之间重合时，接刀痕也 较小。

螺旋角β越小，则切削力越大；β越大，则切削力越小。所以，高速立铣时，应适当增大刀具的螺旋角。

铣削中运用最少量润滑技术(MQL)，可减少刀具—工件和刀具—切屑之间的摩擦，起到抑制温升、降低刀具磨损、防止黏结、提高加工质量的作用。试验结果表明：MQL辅助切削的刀具磨损量、加工表面粗糙度及切削力都与湿切削的相当，而且被加工表面的毛刺明显比湿切削的少。

3 结论

(1) 用三层改进的 BP神经网络对切削力进行预测，通过模具现场加工证明所建立的铣削力预测模型具有较高的预测精度。

(2) 主轴转速为1.85×104r/min、轴向切削深度为0.09 mm、径向切削深度为0.04 mm、进给速度为2.8 m/s和微量润滑液量为140 mL/h时，切削力较小。

(3) 采用高转速、小切深、合适的进给速度以及微量切削液状态下注塑成型模具进行硬态高速铣削效果好。

(4) MQL辅助切削的刀具磨损量、加工表面粗糙度及切削力都与湿切削的相当。

[1] Ehmann K F, Kapoor S G, Devor R E, et al. Machining process modelling: A review[J]. Journal of Manufacturing Science and Engineering, 1997, 119(4): 655−663.

[2] Takashi M. Effect of tool stiffness upon tool wear in high spindle speed milling using small ball end mill[J]. Journal of the International Societies for Precision Engineering and Nanotechnology, 2001, 25(2): 145−154.

[3] Kim G M, Cho P J, Chu C N. Cutting force prediction of sculptured surface ball-end milling using Z-map[J]. International Journal of Machine Tools & Manufacture, 2000, 40(2):277−291.

[4] Li H Z, Zhang W B, Li X P. Modelling of cutting forces in helical end milling using a predictive machining theory[J].International Journal of Mechanical Sciences, 2001, 43(8):1711−1730.

[5] Lee T S, Lin Y J. A 3D predictive cutting-force model for end milling of parts having sculptured surfaces[J]. Int J Adv Manuf Technol, 2000, 16(11): 773−783.

[6] Lee P, Altintas Y. Prediction of ball-end milling forces from orthogonal cutting data[J]. Int J Mach Tools Manufact, 1996,36(9): 1059−1072.

[7] Yun W S, Cho D W. Accurate 3-D cutting force prediction using cutting condition independent coefficients in end milling[J].International Journal of Machine Tools & Manufacture, 2001,41(4): 463−478.

[8] Fuh K H, Hwang R M. A predicted milling force model for high-speed end milling operation[J]. Int J Mach Tools Manufact,1997, 37(7): 969−979.

[9] Azeem A, Feng H Y, WANG Li-hui. Simplified efficient calibration of a mechanistic cutting force model for ball-end milling[J]. International Journal of Machine Tools &Manufacture, 2004, 44(2/3): 291−298.

[10] Ikua B W, Tanaka H, Obata F, et al. Prediction of cutting forces and machining error in ball end milling of curved surfaces (Ⅱ):Experimental verification[J]. Journal of the International Societies for Precision Engineering and Nanotechnology, 2002,26(1): 69−82.

[11] Sarhan A, Sayed R, Nassr A A. Interrelationships between cutting force variation and tool wear in end-milling[J]. Journal of Materials rocessing Technology, 2001, 109(3): 229−235.

[12] Bao W Y, Tansel I N. Modeling micro-end-milling operations(Ⅰ): Analytical cutting force model[J]. International Journal of Machine Tools & Manufacture, 2000, 40(15): 2155−2173.

[13] 刘志新. 高速切削过程动力学建模及其物理仿真研究[D]. 天津: 天津大学机械工程学院, 2006: 17−18.

LIU Zhi-xin. Research on dynamic modeling of high speed cutting process and its physical simulation[D]. Tianjin: Tianjin University. College of Mechanical Engineering, 2006: 17−18.

[14] 王凌云, 黄红辉. 注塑成型模具硬态铣削表面粗糙度研究[J].中南大学学报: 自然科学版, 2009, 40(6): 1604−1608.

WANG Ling-yun, HUANG Hong-hui. Surface roughness of plastic mold parts in finish hard milling[J]. Journal of Central South University: Science and Technology, 2009, 40(6):1604−1608.

(编辑 刘华森)

Milling force of plastic mold parts in high speed hard milling based on BP neural network

WANG Ling-yun, HUANG Hong-hui

(Department of Manufacturing Engineering and Technology, Shanghai University of Engineering Science,Shanghai 200437, China)

Taking the hard milling of the plastic mold parts (cavity) as an example, using a hardened 4Cr5MoSiV1 steel and AlTiN coated carbide end-milling tool, the empirical model of the cutting force model was carried out with the improved BP neural network and a multi-factorial orthogonal test, the accuracy of the cutting force network prediction was examined by field-processing practice (practice of hard milling of the mold parts). The results show that the artificial neural network can predict the size of milling force well and has strong generalization ability and adaptive capacity; the smaller milling forces can be attained by using higher spindle speed, appropriate feed rate, lower axial and radial depth of milling parameters as well as minimum quantity of lubricant (MQL), which provide a better basis for cutting parameters optimization of hard milling of the plastic mold parts and its manufacture.

hard milling of mold parts; improved BP neural network; milling force model; parameters optimization

TH16；TH161+.1

A

1672−7207(2010)06−2218−06

2010−09−01；

2010−10−08

上海市教委自然科学基金资助项目(gjd-07050)；上海工程技术大学科技发展基金资助项目(2008xy60)

王凌云(1963−)，女，湖南湘阴人，教授，从事数控技术应用、先进制造技术、CAD/CAM 等研究；电话：13501979635；E-mail:wanglyun16@sina.com