桥梁防洪评价壅水计算方法浅析
李江海
(吕梁市横泉水库建设管理局,山西 吕梁市 033000)
1 问题的提出
根据《中华人民共和国防洪法》等有关规定,跨河道修建桥梁等建筑物时,应就洪水对建设项目可能产生的影响和建设项目对防洪可能产生的影响作出评价,编制防洪评价报告,提出防御措施。按照《河道管理规范内建设项目防洪评价报告编制导则(试行)》,防洪评价报告包括六大内容,其中作为防洪评价报告重要组成部分的防洪评价计算,主要包括水文分析计算、壅水分析计算、冲刷和淤积分析计算、河势影响分析计算等内容。根据目前山西省编制的防洪评价报告来看,大部分防洪评价计算都有较成熟和统一的计算方法,但桥梁的壅水分析计算方法种类繁多,计算结果差距较大,因此有必要提出较为合理的壅水计算方法。常用的壅水计算公式主要有水面曲线公式、无底坎宽顶堰公式和公路桥涵设计手册《桥位设计》中的两个壅水计算公式,下面着重分析上述四种方法的优缺点和适用条件。
2 壅水计算作用
通过对河道内修建桥梁前后的水面曲线分析,计算出建桥后最大壅水高度、壅水位置和壅水长度,由此不仅可以复核桥梁的建设高度和两岸堤防的高度是否满足行洪要求,还可分析得出建桥后对防汛抢险和桥址河段上下游其他河道及建筑物的影响程度,在此基础上提出相应的防治和补救措施,作出防洪综合评价。
3 壅水计算方法比较
为计算建桥后河道的壅水情况,首先需计算建桥前的天然河道水面曲线,以便与建桥后的水面曲线进行比较,确定壅水高度。关于建桥前的天然河道水面曲线计算,在各类防洪评价报告中方法较为统一,即
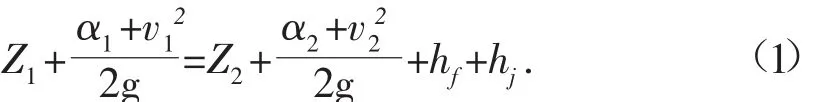
式中:Z1,Z2——上下游断面的水位,m;
v1,v2——上下游断面的流速,m/s;
α1,α2——上下游断面的动能修正系数;
hf,hj——沿程水头损失和局部水头损失,m。
一般河道均为缓流,水面曲线应从下游向上游通过试算推求。为了分析建桥后的壅水情况,天然河道水面曲线计算分段时,除按公式应用要求确定计算断面外,还必须将桥址处和初估最大壅水高度位置作为计算断面。对于建桥后桥梁的壅水计算,常用的公式有以下四种:
3.1 水面曲线公式
计算公式仍采用式(1),通过对建桥前后水位的比较可得出壅水高度,但需考虑因桥梁阻水产生的局部水头损失。在实际计算中,采用该方法的优点是:该公式作为水力学水面曲线计算中的基本公式,在各行业中得到普遍应用,特别是在河道规划等计算精度要求不高的工程中,计算过程较为简便。缺点是:局部水头损失较难确定,如桥墩长宽比不等于4时,局部水头损失系数无明确取值,另外河槽内新建桥墩对原过水面积的减小、桥下回流区域产生的无效过水面积与湿周、桥墩方向与水流方向夹角不同等因素也会影响局部水头损失系数的取值,但这些因素在该公式中得不到直接体现,虽然上述部分参数可参照《桥梁水力学》等资料中的有关公式确定,但计算过程较为繁琐。对于比较顺直的河道采用明渠均匀流公式,而绝大多数天然河道由于形状不规则,且调蓄作用不明显,一般采用下列恒定流水面曲线公式进行计算:
3.2 无底坎宽顶堰公式
无底坎宽顶堰公式计算公式为:

式中:Q——过桥流量,m3/s;
σ——淹没系数;
m——流量系数;
b——桥净长度,m;
H0——上游流速水头,m。
根据上游流速水头和上游断面即可计算出上游水深,得出壅水高度。该方法的优点是计算简单,缺点是必须满足使用条件,即桥宽与上游水深的比值必须在0.67~2.5之间;壅水位置在3~5倍的上游水深之间,但具体位置难以确定,一般仅用于矩形断面,而不规则的天然河床断面计算相当复杂。所以式(2)多用于影响不大且过水断面为矩形的小桥涵壅水计算。
3.3《桥位设计》公式之一
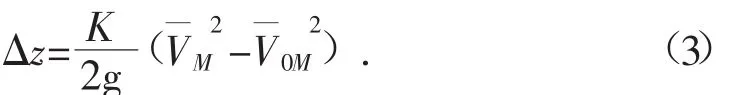
3.4《桥位设计》公式之二

式中:Δz——桥前最大壅水高度,m;
η——系数;
4 结语
式中:Δz——桥前最大壅水高度,m;
K——壅水系数;
通过对以上四种壅水计算公式的分析可知:在推求整个河道水面曲线计算中,对最高壅水位与桥墩的准确距离等要求不是很高,所以部分因素可以忽略,此时采用水面曲线计算公式较为简单,但对于防洪评价中的桥梁壅水计算,精度要求相对较高,若采用该公式进行计算,不仅计算过程复杂,而且要求的计算参数较多,一般难以满足,故防洪评价计算中要慎用;对于矩形过水断面的小桥涵可采用式(2);对于资料比较齐全的工程可采用式(3);对于资料不全、精度要求不是很高的工程可采用式(4)。上述桥梁壅水计算公式主要适用于缓坡河道,陡坡河道一般不会出现很长的壅水,主要应考虑桥墩的水流冲击高度。由于桥梁实际水流非常复杂,目前壅水计算中有的公式是对许多影响水流的因素进行了简化甚至予以忽略,大多属于理论与经验相结合的公式,使得计算结果或多或少与实际情况有所不同,因此,对于所在河段有重要防洪任务或对河势稳定可能产生较大影响的桥梁,在采用上述公式进行防洪评价壅水分析时还应通过数学模型计算或物理模型试验复核计算结果。

