动态滑模控制在并联机器人中的应用
朱彩红
(苏州市职业大学 电子信息工程系,江苏 苏州 215104)
并联机器人同串联机器人相比,具有刚度大、承载能力高、精度高、结构紧凑等特点,可广泛应用于工业、航空、军事等领域[1].最近几十年,国内外学者对并联机器人的特点、机构学、运动学方面进行了广泛、深入的研究.但是,并联机器人作为一个结构复杂、多变量、多自由度、多参数耦合的非线性系统,其控制策略、控制方法的研究极其复杂.最初设计控制系统时,大多把并联机器人的各个分支当作完全独立的系统来进行控制,控制策略为传统的PID控制,控制效果很不理想.模糊控制方法可以在不要求机器人模型精确的情况下实现机器人的控制,但是模糊控制方法的模糊规则设计比较重要,规则设计的好坏将会直接影响到控制的效果[2],而且该规则的设定需要具有专家知识或是经过多次试验得到,因此在没有相应的条件下,该方法可能无法起到较好的控制效果.
滑模变结构控制本质上是一类特殊的非线性控制,其非线性表现为控制的不连续性,这种控制策略与其他控制策略的不同之处在于系统的“结构”并不固定,而是在动态过程中根据系统当前的状态(如偏差及其各阶导数等)有目的地不断变化,迫使系统按照预定“滑动模态”的状态轨迹运动[3].研究表明[4-6]:滑模变结构控制具有快速响应、对参数变化及扰动不灵敏、无需系统在线辩识,物理实现简单等优点.滑模变结构控制方法比较适合并联机器人控制[7-8],因此本文采用了一种新的机器人轨迹跟踪变结构控制方法,即基于动态切换函数的动态滑模控制方法,亦即通过设计新的切换函数或将常规滑模变结构控制中的切换函数s通过微分环节构成新的切换函数σ,该切换函数与系统控制输入的一阶或高阶导数有关,可将不连续项转移到控制的一阶或高阶导数中去,得到在时间上本质连续的动态滑模控制律,可以有效地降低抖振.
1 滑模控制器的设计
滑模变结构控制器的设计需要完成以下的工作: 切换函数s(x)的求取;保证滑动模态的存在;滑动模态稳定性的确定;变结构控制趋近阶段的鲁棒性及动态品质的保证;变结构控制的寻求.
考虑如下单入单出n阶仿射非线性系统:

式中:x∈R为可测状态变量;u,y∈R分别为系统的输入和输出;f(x),g(x)为已知平滑函数;η为系统中的不确定项,它包括模型不确定性和外加扰动[9].
定义误差及切换函数分别为:

式中:ei=e(i-1)(i=1,2,…,n)为跟踪误差及其各阶导数,选取常数c1,c2,…,cn-1,使得多项式pn-1+cn-1pn-2+…+c2p+c1为Hurwite稳定,p为Laplace算子.则

构造新的动态切换函数

式中λ为严格的正常数.
假设1 不确定性满足有界条件,存在有界函数Bn(x),使得│η│≤Bn(x),x∈Rn,且g(x)符号恒定.
假设2 不确定项导数有界即

假设3 存在正实数ε,满足

动态滑模控制律取为

稳定性分析:稳定性是系统的一个基本结构特性,稳定性问题是系统控制理论研究的一个重要课题.
将式(2)代入式(4)得

则

将式(1)、(2)代入式(9)整理得

将控制律式(7)代入式(10)得

则根据假设1~3得

通过李亚普诺夫稳定性分析,得出新的动态切换函数σ满足,即满足滑模变结构控制理论的到达条件,从而验证了系统的稳定性,也就保证了控制器的鲁棒性和动态品质.
2 并联机器人控制模型的建立
本文研究的少自由度并联机器人具有各支路机构简单,不存在虚约束及工作空间较大等特点[10].
机器人系统完整的拉格朗日动力学模型为:

由于式(12)已写成拟线性化的形式,看上去比较简洁.实际上,在本研究的系统中式(12)的展开形式相当复杂.基于机器人关节或支路模型的分散控制系统是目前应用最为广泛的设计方法之一,在工业工程中绝大部分的机器人系统都采用了该类设计方法.
对于本文所研究的并联机器人,相互并联的各支路可用图1表示.
当机器人关节的驱动装置为交流伺服电机,且忽略等效干扰力矩,可导出机器人各支路的数学模型传递函数为

图1 机器人支路模型

式中:J'=Lp(Ja+Jm+i2J0);B'=(Rp+KAKi)(Ja+Jm+i2J0)+Lp(Bm+i2B0);W'=(Rp+KAKi) (Bm+i2B0);Kx=3K2tp/2;K=3KAKpreKtp/2.
3 实例仿真及分析
机器人的交流伺服电动机参数为:Kpre=88,Ki=2.2,KA=6,Ktp=3.41 N·m/A,Lp=0.038 37 H,Rp=5.09 Ω,Ja=0.19 kg·m2,取减速装置的速比为i=40,关节部分在减速装置驱动侧的转动惯量为0.1 kg·m2.由于机构间的耦合作用,系统的等效转动惯量和等效负载阻力系数取J0=40,B0=0.取Jm=0,Bm=0.
由此可得交流伺服驱动机器人关节的模型传递函数为
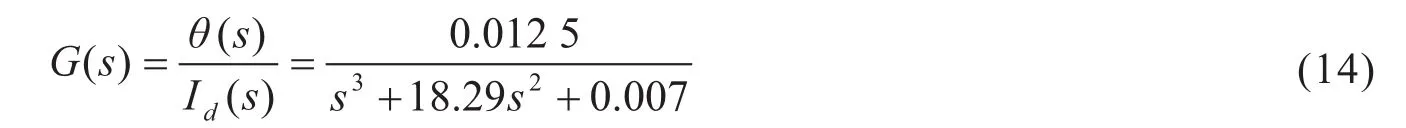
转换为状态方程,则有

这里f(x)=-0.007x1-18.29x3,g(x)=0.012 5.
设期望的跟踪信号为yd=sint,跟踪误差为e=x(1)-yd.n=3时,定义s=c1e+c2+c3,取c1=c2=100,c3=1,λ=3 000,初始条件为x(0)=[0.5 0 0],则动态控制律为:
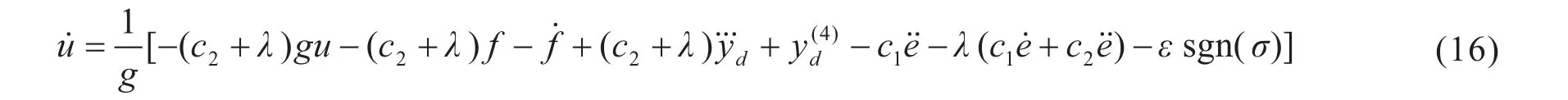
以Matlab/Simulink构成仿真模型,其中包括两个S—Function,仿真采用ode45,步长0.001 s.仿真结果如图2所示.

图2 仿真结果
4 结 论
仿真结果表明,所采用的机器人轨迹跟踪滑模变结构控制方法,即基于动态切换函数的动态滑模控制,具有良好的抗干扰作用和跟踪性能,其研究为进一步实现该并联机器人机构的高精度实时控制奠定了基础.
[1] PIEPER J.First order dynamic sliding mode control:Decision and Control,Tampa,December 16-18,1998[C].New York:IEEE Press,c1998.
[2] HWANG Chihlyang,CHANG Lijui,YU Yuansheng.Network-based fuzzy decentralized sliding mode control for car-like mobile robots[J].IEEE Trans.on Industrial Electronics,2007,54(1):574-585.
[3] 胡跃明.变结构控制理论与应用[M].北京:科学出版社,2003.
[4] MOON J,KIM K,KIM Y.Design of missile guidance law via variable structure control [J].Journal of Guidance,Control and Dynamics,2001,24(4):659-664.
[5] SATO H,TANAKA M,MATSUNO F.Trajectory tracking control of snake robots based on dynamic model[J].Transactions of the Society of Instrument and Control Engineers,2006,42(6):651-658.
[6] 梅 红,王 勇.快速收敛的机器人滑模变结构控制[J].信息与控制,2009,38(5):553-557.
[7] 吴 博,吴盛林,赵克定.并联机器人控制策略的现状和发展趋势[J].机床与液压,2005(10):5-8.
[8] 王洪斌,王洪瑞,肖金壮.并联机器人轨迹跟踪积分变结构控制的研究[J].燕山大学学报,2003,27(1):25-28.
[9] 刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005.
[10] 许春山,孙兴进,曹广益.一种新的机器人轨迹跟踪滑模变结构控制[J].计算机仿真,2004,21(7):115-118.

