拓展双曲线法在铁路客运专线路基沉降预测中的应用

王小刚,陈善雄,余 飞,王星运

(1.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室,武汉 430071;2.湖北省电力勘测设计院,武汉 430024)

1 概述

合理有效地分析和预测最终沉降量是路基工程的一个重要的课题[1]。路基沉降量的预测方法主要有三类。第一类为经典的分层总和法。第二类为基于固结理论的数值模拟方法,如考虑非线性弹性模型及弹塑性模型的有限元方法等。这二类方法由于计算模型与计算参数与实际有一定的偏差,计算结果与实际情况并不完全相符。第三类为根据实测数据推算沉降量与时间关系的回归拟合法,主要有双曲线法、三点法、Asaoka法、泊松曲线法、星野法、沉降速率法、S型方法、增加曲线法以及各种组合方法等[2～6],但每种方法都有一定的适用范围和局限性,如双曲线法需要采用恒载以后的数据进行预测,因而要求恒载期不能过短；三点法要求选取的恒载后的三点时间间隔相等,且尽可能的大,所以人为取点的影响较大；Asaoka法要经过等时均分等。

德国高铁在双曲线法的基础上,引入荷载系数的概念,形成了拓展双曲线法,并应用于路基沉降预测并取得了较好的预测效果。本文将结合武广铁路客运专线路基现场观测数据,对比拓展双曲线法与双曲线法、三点法、Asaoka法等的预测结果,研究拓展双曲线法时间段合理选取等问题,以评价拓展双曲线法对于我国铁路客运专线路基沉降评估的适用性和有效性。

2 拓展双曲线法介绍

拓展双曲线方法是在常规双曲线法中引入荷载系数拓展而成的,它假定在荷载增量、加载速率变化不大的情况下,沉降变形的增量与荷载增量成正比。该方法与传统方法的最大区别就是将填筑期观测数据纳入分析时间段以内,其基本公式如下

(1)

(2)

式中，ζ为荷载系数；σ为t时刻的荷载水平,σ=hγ,h为填方高度,γ为土的重度；σmax为最大荷载；σmax=Hmax×γ,Hmax为填方最大高度；St为t时刻的沉降量；t为自土方工程开工以来的累计时间；a、b为曲线拟合参数,a为截距,b为斜率。

对(1)式进行变换得

(3)

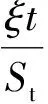
当t→∞时,可以利用直线的斜率计算轨道结构铺设完成后的基底最终沉降量

(4)

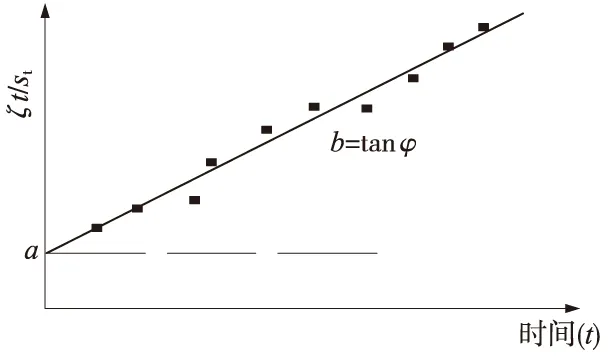
图1 参数a、b的求解

3 拓展双曲线法的适用性分析

3.1 工程概况

武广铁路客运专线正线全长1 068.6 km,设计时速300 km,铺设无砟轨道,无砟轨道要求路基的工后沉降量不大于15 mm,因此,采用CFG桩、柱桩、强夯、压实等地基处理的方式进行地基加固。

选取典型断面DK1 291+364沉降板观测数据进行分析。该断面采用注浆、混凝土桩进行地基加固,2008年1月11日开始填土,第56 d填土完成,累计填土高度为2.85 m,观测至2008年10月7日沉降量为7.56 mm,图2为该断面的H-t-S曲线图。

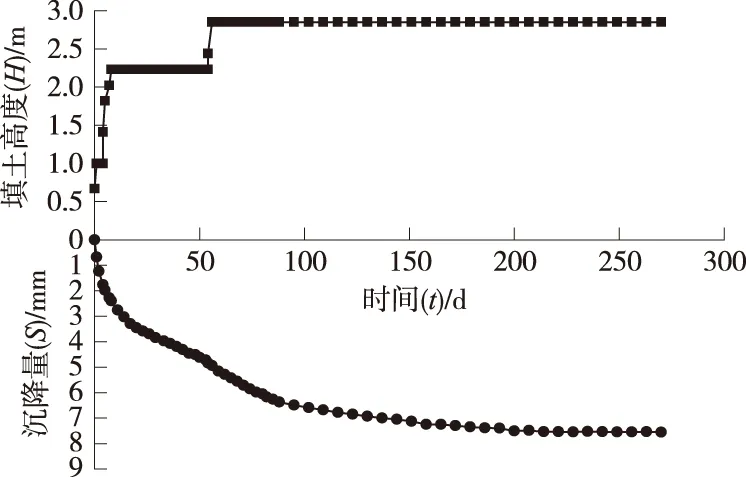
图2 断面DK1 291+364沉降板H-t-S曲线

3.2 不同方法的预测结果对比

(1)拓展双曲线法

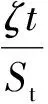
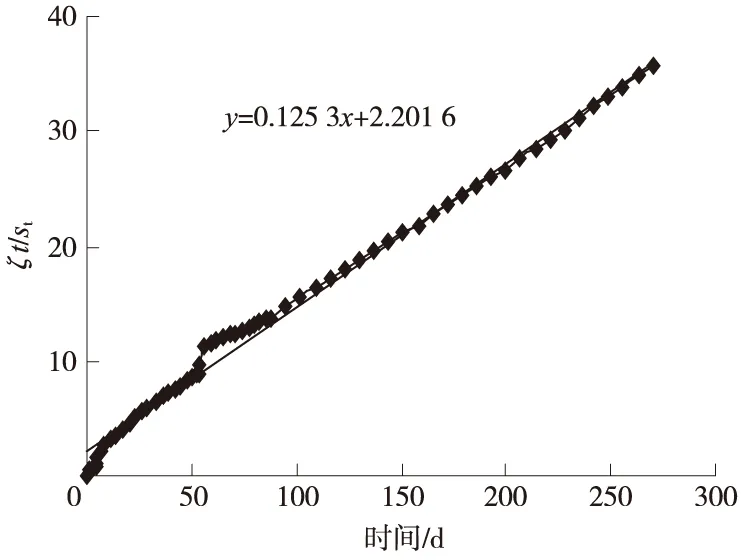
图3 拓展双曲线法直线回归曲线

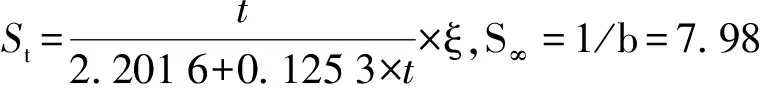
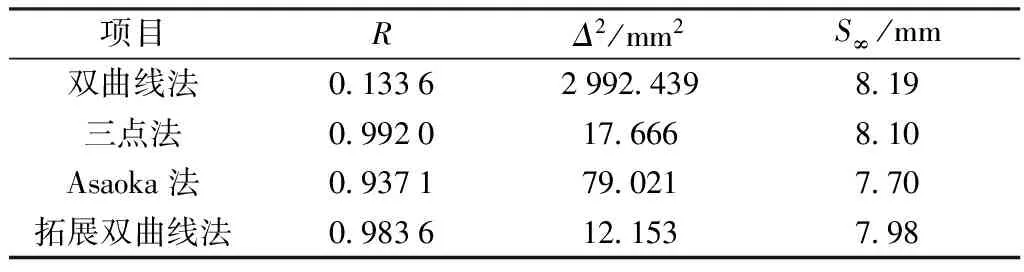
表1 不同预测模型的预测结果对比

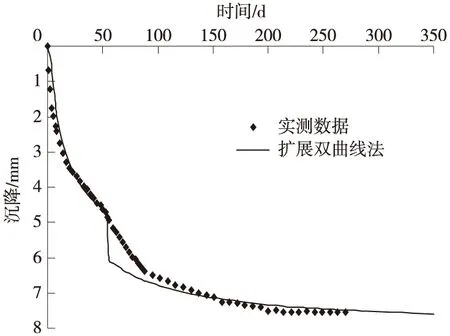
图4 拓展双曲线法的拟合曲线

由于拓展双曲线法中引入了荷载系数的概念,此方法相对于传统方法的最大特点在于它不仅利用了恒载期后的数据,也利用了加载期的沉降观测数据,因此,它对观测期的适用性较强。

由表1和图4的结果分析可知,拓展双曲线法的拟合效果较好,相关系数高,误差平方和小。

(2)其他模型的预测结果

利用常规双曲线法、Asaoka法和三点法等沉降预测模型,对武广铁路客运专线DK1 291+364断面的沉降板0～280 d的沉降观测数据进行拟合预测,得到的结果分别如下。

双曲线法

Asaoka法

St=7.7-7.7e-0.039 641t

St=8.1-6.680 36e-0.016 5t

这几类不同预测模型的相关系数、误差平方和最终沉降量等详见表1与图5。

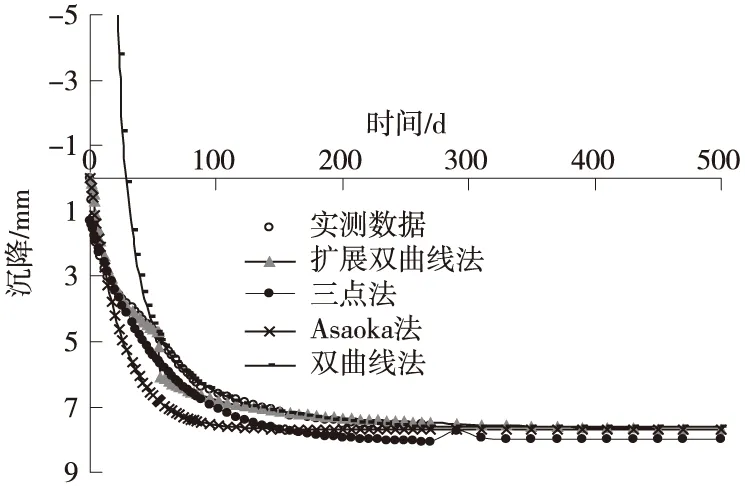
图5 各类沉降预测对比

分析表1和图5可知：

①拓展双曲线法在第50～70 d这段时间内与实测数据偏差略大,这是由于此段时间内,路基上经过一段停载时间后,又发生了二次加载,即此时的荷载增量较大,沉降速率较快,两者不满足线性关系(从图3中可以看到回归曲线偏离直线)。因此,在运用拓展双曲线法时,要特别注意恒载稳定后,又突然加载的情况。从表1中可见,拓展双曲线法的相关系数仅次于三点法。误差平方和在这几类预测方法中为最小。

②双曲线法的拟合曲线前期误差比较大,甚至出现负值(实际上前期的负值比图中所示的更大,大于-5 mm的数据点已省去)。从而导致相关系数很低,曲线的后半段与实测数据的拟合情况较好。

③Asaoka法,三点法的沉降预测曲线整体上在实测曲线的下方,相比于拓展双曲线法,它的预测结果略为偏大。这三类方法误差平方和都比较小,在工程允许的误差范围之内。

(3)拓展双曲线法在观测期较短时的优势

当观测期较短,这里只用0～95 d的观测数据(56～95 d为恒载荷期),此时运用不同的预测方法对比结果如图6所示。

从图上可以看出，20 cm深度土样的连线比较平缓，明显表现出较低的异质性，而0～20 cm深度的平均数据(对5 cm和20 cm深度土样求平均)与GPR数据的平均趋势更为接近，但又失去了当前点位置的异质性，因而，在本实验中，地面直达波的测量深度很有可能小于20 cm。而通过对图3和图4综合分析，GPR的总体测量精度约为0.02 cm3/cm3。

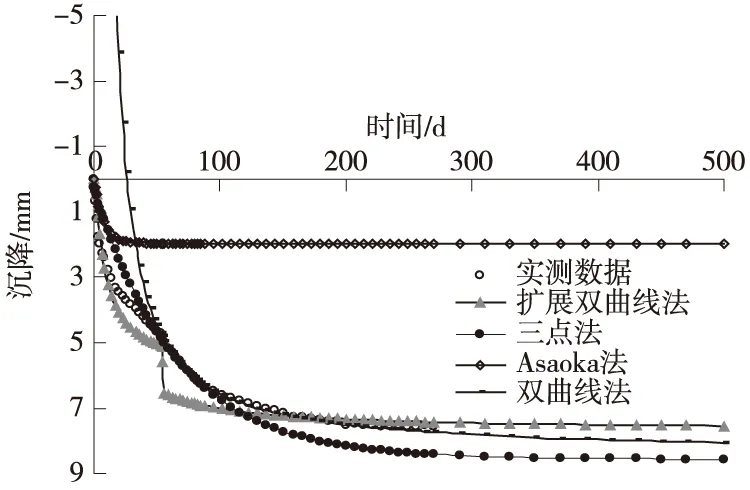
图6 恒载1个月时的各预测方法对比

由图6可知,当观测期较短时,拓展双曲线法相比其他预测方法拟合的效果更好。这主要是由于它引入了荷载系数概念,把加载区的观测数据纳入分析段的原因。而其他方法只利用恒载区的观测数据。因而在观测期较短的时候,拓展双曲线法有着独特的优势。

4 预测精度影响因素分析

4.1 起始终点时间和恒载时间

为更好地运用拓展双曲线法,以下讨论起始时间和恒载期的长短对预测结果的影响。

选定了2个时间起点和3个时间终点,共6个时间段的观测数据来进行预测对比分析,分析结果见表2。其中,t0为加载起始时间；th为停载时间点；tz为评测时间终点；tz-1为评测时间终点前1个月,其他含义照此类推。表中的th～tz为5～7个月。

由表2的分析结果可知：

(1)以停载时间th为起点的数据段,比以加载时间t0为起点的数据段的相关系数高,但两者相差很小,反映了时间起点对回归曲线相关系数影响不大。但恒载期长短对相关系数存在一定的影响,恒载期数据越短,相关系数呈逐步减小的趋势。

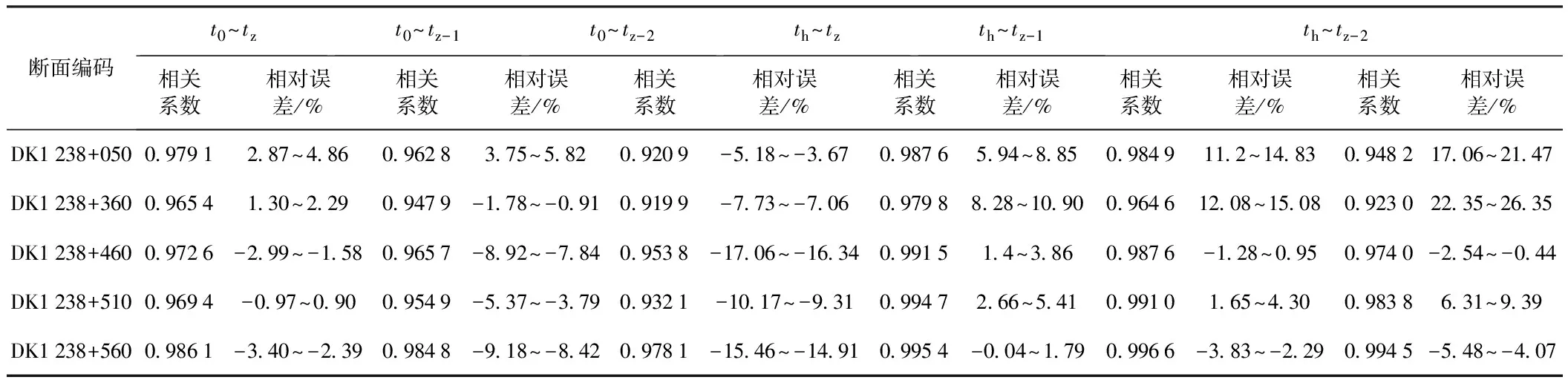
表2 拓展双曲线法回归曲线相关系数与预测误差分析

(2)不同的时间起点对预测误差的影响规律并不明显,但恒载期长短对预测误差存在明显的影响。当选取的时间段包含整个恒载期数据时(t0～tz),预测相对误差在5%以内；当选取的时间段包含的恒载时间缩短1～2个月时(t0～tz-1、t0～tz-2),相对误差明显变大,达到10%～20%或更大些。这就表明,在恒载时间较短的情况下,采用拓展双曲线法进行预测,可能存在较大的误差。因此,采用拓展双曲线法时,恒载观测期不宜小于4～5个月。

4.2 加载期观测频率的影响

对DK1 291+364断面分别取加载期的观测时间间隔为5～7 d(第0、5、11、17、23、29、36、42、48、53 d)和10～14 d(第0、11、23、33、42、56 d)的观测数据作为分析对象,恒载期的所有观测数据都加以利用。进行拓展双曲线法的计算分析，得到结果如表3所示。

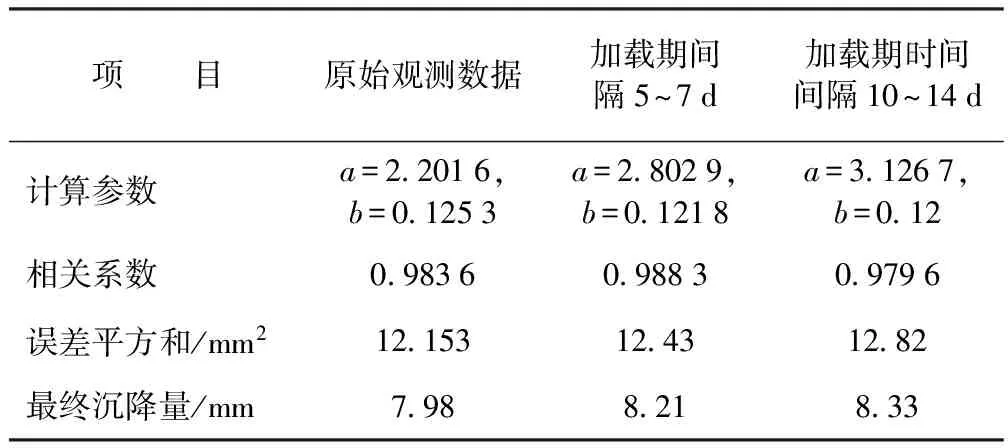
表3 加载期不同时间间隔的拓展双曲线法的结果对比

由表3的分析结果可见,随着加载期的沉降观测时间间隔的增大,误差平方和、最终沉降量都略有增加,相关系数的波动较小。这说明加载期的观测频率在一定范围内(5～10 d观测一次)波动时,对预测结果产生的影响不大。

5 相关系数与相对误差的分析

相关系数和相对误差都是曲线拟合法的重要参考指标,考虑到观测数据的波动性会对回归分析造成很大的影响,致使相关系数不满足要求,或者相对误差过大。本文对DK1 230+310～DK1 238+710段126个路基断面沉降观测数据进行了分析,其相关系数和相对误差结果统计列于表4与图7。

表4 拓展双曲线法相关系数和相对误差统计

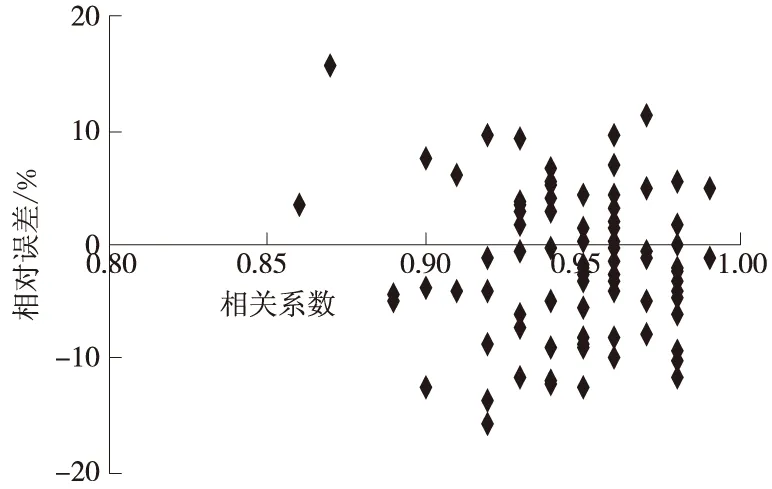
图7 拓展双曲线法相关系数与相对误差

分析表4与图7,不难看出拓展双曲线法的相关系数均在85%以上,有88.0%能满足不小于0.92的要求,可见拓展双曲线法用于路基沉降预测是可靠性的。拓展双曲线法的相对误差在-10%～10%以内居多,所占比例达到86.8%,相对误差最大也在20%以内。相关系数与相对误差未见明显的相关关系。

可见,拓展双曲线法用于路基沉降预测具有良好的适应性,大多数情况下可以取得较好的预测效果,是一种值得推荐的路基沉降预测的方法。

6 结论

根据以上的分析可以得出如下结论：

(1)拓展双曲线法的拟合效果较好,相关系数高,误差平方和小。双曲线法的前期预测曲线偏离实测数据较大,三点法与Asaoka法的预测结果略为偏大。

(2)拓展双曲线法对观测期的适应性较强。但是这种适应性也是有限的,从多个断面的分析结果可知,它的预测误差和恒载期长短密切相关,恒载期越长,预测误差越小。因此,采用拓展双曲线法时,恒载观测期不宜小于4～5个月。

(3)由于拓展双曲线法假定荷载增量、加载速率都比较小,因此,在停止加载后一段时间又突然加载的情况下,即荷载增量突然增大的时候,会出现和实测曲线有较大偏差。

(3)加载期的观测频率对拓展双曲线法的预测结果影响较小。随着频率的增大,误差平方和、最终沉降量都略有减小。

[1]蔡 英.铁路客运专线路基研究[M].成都：西南交通大学,1995.

[2]胡荣光.客运专线路基沉降规律影响因素分析与沉降预测[D].长沙：中南大学,2008.

[3]Mosleh A. Al-Shamrani. Applicability of the rectangular hyperbolic method to settlement predictions of sabkha soils[J]. Geotechnical Geological Engineering, 2004,22:563-587．

[4]金 莉.几种预测模型在高路堤沉降预测中的对比分析[J].西部探矿工程,2006,18(4):234-236.

[5]王志亮,郑明新,吴 勇,等.增加曲线模型在路基沉降预测中的应用研究[J].岩土力学,2004,6(25)：901-903.

[6]潘林有,谢新宇,罗 昕,等.软土地基实测沉降的拟合和预测[J].哈尔滨工业大学学报,2004,34(11)：1474-1475.