仅采用Rx与R滑的大小比较来选择供电电路行吗？

李维兵

(南通高等师范学校 江苏 南通 226100)

电学实验是每年高考实验考查的重点，其中供电电路中限流式和分压式(图1)的选择一直困扰着学生，致使许多学生在考试时失分严重．因此，作为物理教学工作者，我们应该积极钻研，探讨影响供电电路选择的因素，找出解决途径，帮助学生攻克这一难关．

图1

笔者曾见过一篇题为《伏安法的电路设计》[1]的论文，论文的作者对供电电路限流式和分压式的选择做了总结，他仅采用了待测电阻Rx与滑动变阻器R滑的比较来选择电路，方法如下：

(1)当R滑≫Rx时(通常情况下，R滑>10Rx)用限流式．

用分压式．

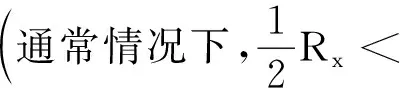
笔者在电学实验教学的过程中发现，文献[1]作者对供电电路所总结的三点，在具体解题过程中并不都适用，仅采用待测电阻Rx与滑动变阻器R滑的大小比较来选择电路具有一定的片面性．下面对此进行探讨．

(1)举例说明

【例题】用伏安法测某金属的电阻(约40 Ω).已知电源电动势为6 V，内电阻约为0.05 Ω；电流表量程为50 mA，内电阻为10 Ω；电压表量程为3 V，内电阻为6 kΩ；滑动变阻器阻值为0～200 Ω．请设计一个实验方案并画出电路图．

解析：按文献[1]作者思路解，因为

假设限流式：估算最小电流

其待测电阻最小电压

Umin=IminRx=1 V

电流和电压均没有超过量程，应该接限流式．

假设分压式：利用欧姆定律可以估算出滑动变阻器的滑片移到不同的位置时，电流表、电压表所对应的值分别为

(1)

U=IR滑

(2)

数据分析计算如表1.

表1

从上面两种方式分析可以看出：选用限流式时，电流表的范围大约在24 ～50 mA之间,电压表大约在1～2 V之间；而选用分压式时，由表格中的估算可以看出，电流表范围在0～50 mA,电压表范围在0～2 V之间．不难发现，采用分压式时，电表读数误差更小，故分压式更合理．因此在限流式和分压式电路的选择上，并不是仅仅采用待测电阻Rx与滑动变阻器R滑进行简单比较就能下定论的．

实际上，在伏安法测电阻的实验中，除了滑动变阻器会对供电电路的选择有影响外，不同的电源、不同量程的电压表、电流表也会对供电电路的选择有影响．

(2)不同的电源对供电电路选择的影响

如上面的例题，设其他条件均不改变，将电源电动势改为3 V，请设计电路．

假设限流式: 估算最小电流

其待测电阻最小电压

Umin=IminRx=0.48 V

电流和电压均没有超过量程，而且当电流表满偏电流

Imax=50 mA

其待测电阻的最大电压

Umax=ImaxRx=2.4 V

假设分压式：利用上面(1)、(2)两式可以估算待测电阻的电流和电压．

数据分析计算如表2.

表2

从上面两种方式分析可以看出：选用限流式时，电流表范围在12 ～50 mA之间，电压表的范围在0.48～2.4 V之间；而选用分压式时，电流表范围大约在0～50 mA，电压表的范围大约在0～2 V，且滑动变阻器从零滑到140 Ω时，电压仅在1 V以内变化，故此时选限流式更好．

再如，设其他条件均不改变，将电源电动势改为12 V，采用限流式，估算最小电流

接近满偏，可知只能采用分压式．可见，选择不同的电源会影响供电电路的选择．

(3)不同量程的电表对供电电路选择的影响

如上述例题，设其他条件均不改变，将电流表量程改为100 mA，电压表量程改为6 V，请设计电路．

假设限流式:估算最小电流

其待测电阻最小电压

Umin=IminRx=1 V

当电流表满偏电流

Imax=100 mA

其待测电阻的最大电压

Umax=ImaxRx=4 V

其滑动变阻器此时电阻

R滑=0 Ω

假设分压式：电流和电压的变化如表1所示，从表1中可以看出，滑动变阻器的电阻R滑从0～180 Ω间，电压的范围基本集中在0～3 V之间，大约为满偏的一半．

相比之下，此时选限流式更为合理．可见不同量程的电表会影响供电电路的选择．

由此可见，在电学实验设计电路的过程中，供电电路的选择受到滑动变阻器、电源、电压表、电流表等诸多因素的影响．因此，实验设计灵活多变、难度大．虽然我们无法下定论来简单的判断，但可以通过估测判断的方法，来解决这一难题．该过程分三步走，第一步根据待测电阻的大小估测电流表、电压表的范围来选合适的电表；第二步假设限流式，估算出电压、电流的范围，再假设分压式，设滑动变阻器滑到一些位置(如表1所示)，估算出电压、电流的范围；第三步对上述估算进行比较，哪一种估算出来的电表的范围与所选用的电表的量程更符合，就应该选哪一种连接方式．

总之，供电电路的选择是灵活多变的，仅通过Rx与R滑的比较来选择供电电路是不行的．我们只有估算判断比较后，才能选出最合理的方式．

参考文献

1 赵金平,伏安法的电路设计.中学物理教与学.2009(1)：18