“田字变化”类型的网络电路求解

顾春杰 王军明

(奉化市奉化中学 浙江 奉化 315500)

在高中物理恒定电流一章中，我们总会讨论二端无源电阻网络求等效电阻的问题．其中“田”字形网络出现较多，小小“田”字可以有“大变化”.图1是一个田字形电阻网络，先不妨把A1、A2、A3、A4称为“顶”，把B1、B2、B3、B4称为“腰”，而O称为“心”．则可把“田”字形网络分为，顶-顶；腰-腰；顶(腰)-心；顶-腰，共4大类，8种变化形式．

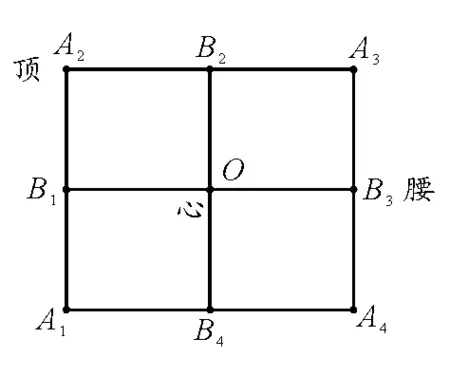
图1 田字形电阻网络

根据“田”字网络的对称性，假设两端加上电压，总能找到电势相等的点，那么就可以将接在等电势节点间的导线或电阻断开(即去掉)，也可以用导线或电阻将等电势节点连接起来，此种处理所得电路与原电路等效．

下面我们一一讨论．

1 “顶-顶”作为二端网络的端口

1.1 对角顶点间等效电阻

已知“田”字形电阻网络每边的电阻均为R，求A1、A3间的等效电阻．(以下求解问题类同)

分析与解1：假设A1A3两端加电压，电流从A1流进，A3流出，因为网络相对A1A3连线对称，故中心O点可断开，如图2所示.利用电阻的串并联知识易得，A1A3间等效电阻

图2

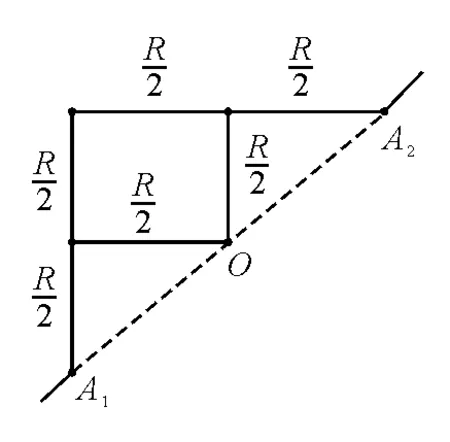
图3

1.2 相邻顶点间等效电阻

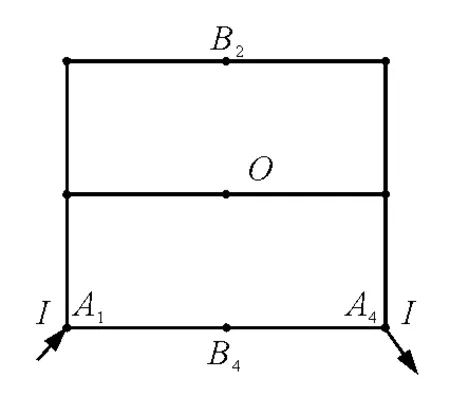
图4

2 “腰-腰”作为二端网络的端口

2.1 相邻腰间等效电阻

图5

2.2 相对腰间的等效电阻

分析与解：假设B1B3两端加电压，电流从B1流入，B3流出，此情景与1.2小节情形相似，B2、B4、O都是等势点，处理方法亦相同，如图6所示电路.利用串并联知识易得B1B3间等效电阻RB1B3=R.

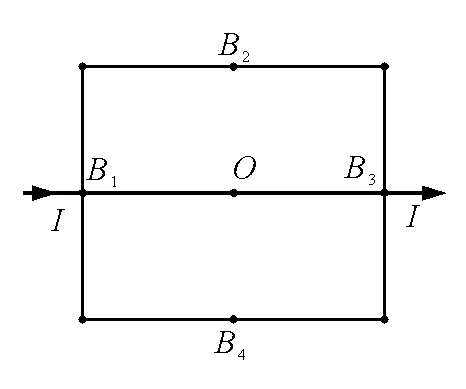
图6

3 “顶(腰)-心”作为二端网络的端口

3.1 顶对心的等效电阻

图7 图8

3.2 腰对心的等效电阻

图9 图10

4 “顶-腰”作为二端网络的端口

4.1 相邻顶腰间的等效电阻

图11

图12 图13

分析与解：图11是一个不对称的问题，针对这种不对称情况，我们设法把它转化为对称的情形.运用叠加原理，图11相当于图12和图13两种对称情况的叠加，此种处理与原情况等效．分别算出两种对称情况下流过A1B4边的电流，叠加得图11中流过A1B4边的电流，再利用UA1B4=RA1B4×I，求解等效电阻RA1B4．

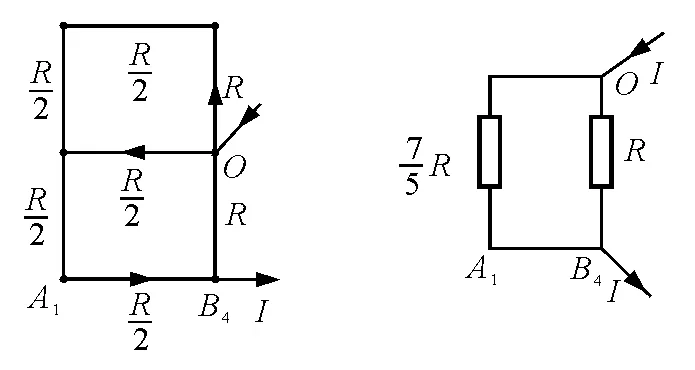
图14 图15

4.2 相间顶腰间的等效电阻

图16

图17 图18

图19 图20

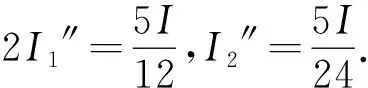
5 拓展：看似不是“田”字形电阻网络的问题

三只相同的金属圆圈，两两正交的连成图21(a)所示的形状．若每一只金属圈原长的电阻为r，试求图中A、B两点间的等效电阻RAB．

图21

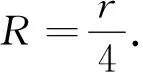
以上我们讨论了“田”字形无源二端网络的8种变化及立体网络可转化为“田”字形网络的情形.分析归纳得出“田”字形无源电阻网络处理的一般方法：假设二端加上电压，电流从网络一端流进，另一端流出，根据电路的对称性找到电势相等的一系列点，采用“断开、去除、折叠”等手段简化网络，利用简单串并联电路的规律求解等效电阻，较为复杂的情况需要用到电路的叠加原理和求解电流分布来确定等效电阻．事实上在求解具体问题时，往往多种手段集于一题，问题才能解决．以上是笔者在指导竞赛过程中的一点不成熟的思考，还望各位物理同仁批评指正．

参考文献

1 范小辉.新编高中物理奥赛指导.南京：南京师范大学出版社，2008

2 程稼夫．中学奥林匹克竞赛物理教程·电磁学篇.合肥：中国科学技术大学出版社，2004