一道机械能守恒定律习题的解析

陆一娣

(江阴市教师进修学校 江苏 江阴 214400)

高中物理教学中，教师需要创设一种教育情境，让学生在感性的体验中提高能力.现以一道力学题目为例，谈谈物理解题思路中运用数学知识使解题变成严谨、更形象的教学过程.

【例题1】如图1所示，在横截面为半圆形半径为R的光滑固定柱面上，用一根不可伸长的细绳分别系小球A和B两侧.已知mA=2mB，开始时A、B静止且与圆柱轴心同高，A球可竖直向下运动，然后释

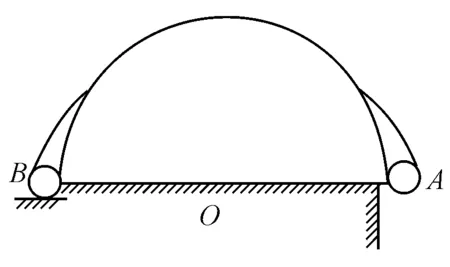
图1

放A球.求小球B到达柱面最高点的速率.应用机械能守恒定律学生可以列出方程并求得结果.

(1)

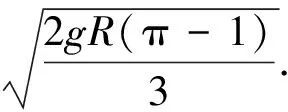
学生作图(图2)并列出方程

进而求得

对以上的结果学生愕然！在惊奇地探究过程中学生们意识到，事实上B球在尚未到达顶点时就已经脱离了圆柱面轨道，因此本题是一道错题！在充分肯定学生们大胆、正确的意见基础上，老师鼓励学生们把本题加以修改，这时学生大脑即刻进入兴奋状态，并产生了一种创造意识，在热烈的学习氛围中，一个富于新意的题目2创造出来了.

【例题2】在例1中去掉已知条件mA=2mB，并由静止起释放A球.若要使B球能沿圆轨道通过半圆顶点，则A和B的质量mA、mB应满足怎样的条件(此时A球尚未着地)？

师生们初步分析：首先要使B球起动必须mA>mB.释放A球后，B球从静止开始沿光滑圆柱面上升并到达顶点，由于柱面光滑，系统机械能守恒.由题意得

(2)

B球在顶点而不脱离圆轨道时

(3)

由式(2)、(3)解得

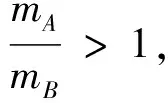
(4)

运用类比思维的方法讨论上述解题过程，可以发现以上分析仅仅考虑了B球在顶点位置时不离开轨道.而这并不能保证其在起点到顶点过程中始终不脱离圆轨道，因此上述解法有不够严谨.

运用严密的数学知识讨论，本题的规范解法应为：设B球在任意位置M(θ角)时速度为v，如图3所示，则

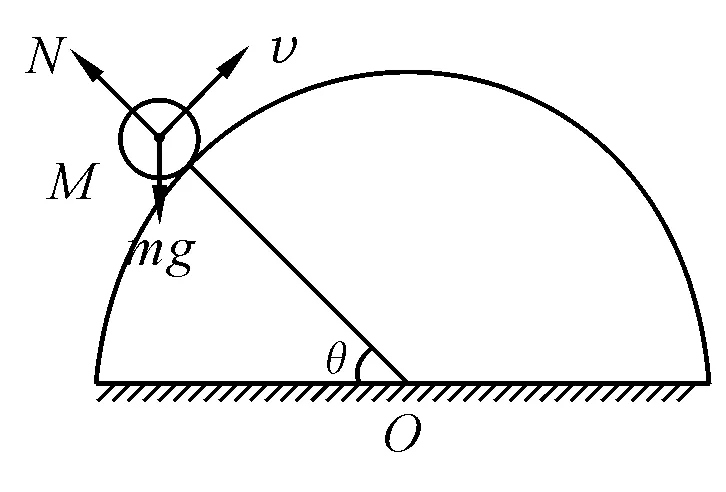
图3

(5)

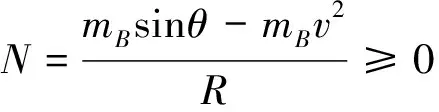
(6)

由式(5)、(6)解得

(7)

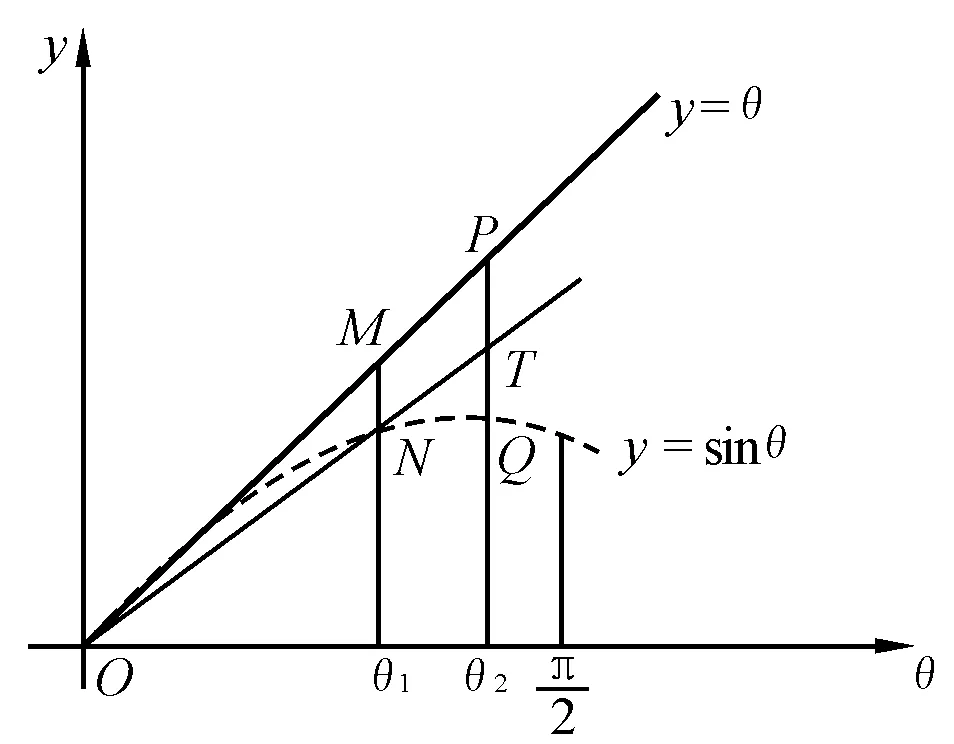
图4

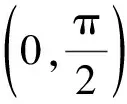
所以

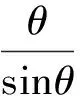
整理得

(8)

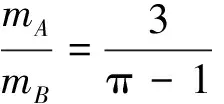
上述解题过程十分严谨，无懈可击.

下面继续运用数学知识对本题作进一步的讨论，以求对本题的物理过程作更深层次的研究、探讨，使物理意义更直观明了.

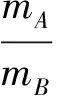
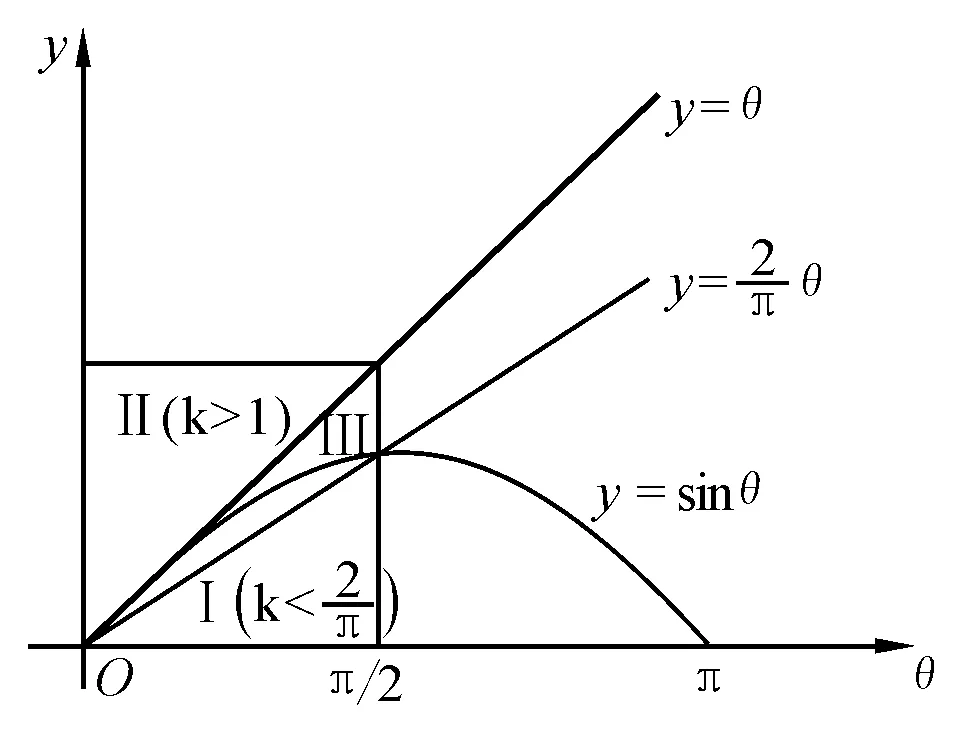
图5

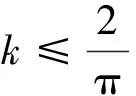
即

此即为本题所求的结果，小球B始终沿圆轨道运动且能过顶点.

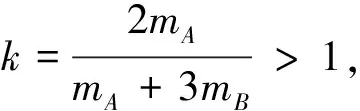
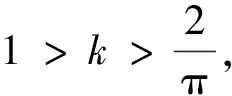
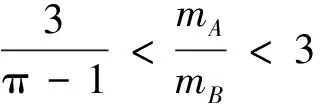
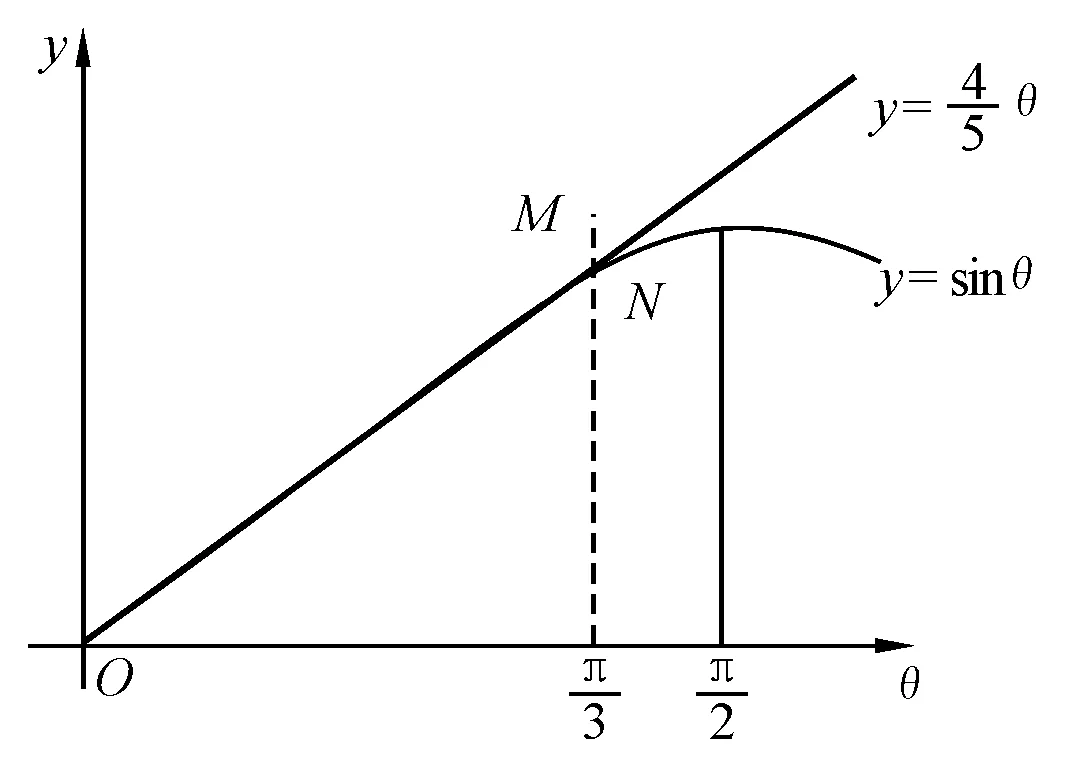
图6

“要给学生一滴水，教师必须常流水”.要培养学生的创新能力，教师首先应是一个不断的创新者.教师要营造一种生动活泼的教育氛围，培养学生积极主动去思维，造就符合时代发展的创新型人才.