迈克耳孙干涉测波长的不确定度分析

赵中华

(辽宁地质工程职业学院 机电系 辽宁 丹东 118008)

赵 杰

(辽东学院 机电学院 辽宁 丹东 118003)

B类不确定度

总不确定度[6～7]

本文分析了测量波长过程中误差的来源，认为文献[6]、[7]计算波长不确定度的方法不妥，并提出新的比较合理的波长不确定度计算方法.

1 在计算波长不确定度方面现有教材存在问题的分析

迈克耳孙干涉测量波长实验原理：设λ为待测波的波长，Δd为变化N个条纹M1移动的距离，是M1的初始位置与末位置的差，则待测光波的波长

波长是间接测量的物理量.

由误差理论知道对物理量的测定需要对测量结果进行不确定度评价，物理量分为直接测量和间接测量量.直接测量与间接测量的标准不确定度的计算方法是不同的.直接量的标准不确定度来源于多次重复测量的A类不确定度，和由仪器误差引入的B类不确定度，而间接测量量的标准不确定度是由各直接测量的标准不确定度传递而来，由传递公式来计算.文献给出的波长不确定度的计算方法适于直接量的不确定度计算，而不适于求间接测量量的不确定度，显然将波长看作直接量来计算是不合理的.本实验中波长是间接测量量，其不确定度应由直接量的标准不确定度传递而来.

2 不确定度分析

2.1 误差的来源

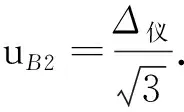
2.2 物理量Δd的测量不确定度

2.2.1 物理量Δd的测量可认为是等精度测量

采用逐差法进行数据处理时，将数据前后平分为两组，前后两组d值之差Δd是间接测量量，其标准不确定度是由各直接量di的不确定度传递而来的.

因为Δdi=d2i-d1i，由间接量不确定度传递公式可得

则有

u(Δd1)=u(Δd2)=…=u(Δdi)=…

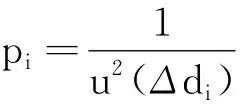
2.2.2 Δd的测量不确定度

因为Δd的测量可认为是等精度测量，则Δd的最佳值

(1)

A类不确定度

(2)

B类不确定度

(3)

总不确定度

(4)

2.3 波长不确定度计算

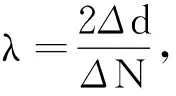
(5)

波长的不确定度由Δd和ΔN(干涉条纹改变数)的标准不确定度传递而来的，

本实验认为N是可以精确测量的，ΔN是等间距的，它的测量误差非常小以至可以忽略.则

(6)

3 实验数据处理

3.1 实验数据

我校迈克耳孙干涉仪型号为GS-1，采用氦-氖激光光源.在调节好仪器后，记下M1镜的初始位置读数d0,继续沿原方向转动微调手轮，每涌出50个圆环干涉条纹记录一次M1镜的位置读数d，连续测量9次，记下9个d值.将数据d0至d9共10个数据,前后平分为两组，用逐差法求出干涉条纹涌出的条纹数ΔN=250时，移动镜M1移动的距离Δd，数据见表1.

表1 迈克耳孙干涉仪测量波长数据

3.2 数据处理结果

3.2.1 Δd的测量处理结果

Δd可近似看作等精度测量，由公式(1)可得

由公式(2)并作t因子修正，可得A类不确定度

1.14×1.2×10-4mm=1.37×10-4mm

仪器最大误差为2%，由公式(3)可得B类不确定度

9.1×10-4mm

由公式(4)可得总合成不确定度

3.2.2 波长λ的测量结果

由公式(5)得λ平均值

6.329 3×10-4mm

由公式(6)可得相对不确定度

7×10-6mm

3.2.3 实验结果表示

参考文献

1 郑建洲.大学物理实验.北京：科学出版社，2007.167～174

2 彭庶修，朱华.大学物理实验教程.北京：国防工业出版，2006.87

3 潘小青.大学物理实验教程.上海：华东理工大学出版社，2005.170

4 赵维义.大学物理实验教程.北京：清华大学出版社，2007.194

5 徐建强.大学物理实验.北京：科学出版社，2006.229～236

6 张志东，魏怀鹏.大学物理实验(第二版).北京：科学出版社，2007.262

7 原所佳.物理实验教程.北京：国防工业出版社，2006.187

8 沈元华.基础物理实验.北京：高等教育出版社，2003.11