多重共线性的检验及对预测目标影响程度的定量分析

张 玲

(辽宁地质工程职业学院,辽宁 丹东 118008)

1 问题的提出

在多元线性回归模型经典假设中，其重要假定之一是回归模型的解释变量之间不存在线性关系，也就是说，解释变量X1，X2，……，Xk中的任何一个都不能是其他解释变量的线性组合.如果违背这一假定，即线性回归模型中某一个解释变量与其他解释变量间存在线性关系，就称线性回归模型中存在多重共线性.多重共线性违背了解释变量间不相关的古典假设，将给普通最小二乘法带来严重后果.多重共线性包含完全多重共线性和不完全多重共线性两种类型.理论上可以证明，当回归方程中的某些变量之间完全相关时，回归系数不存在；当自变量之间高度相关时，回归系数表现出不确定性，从而使回归系数的标准差大大增加.从应用角度看，由于多重共线性的存在，如果仅从回归系数的经济意义出发去解释经济现象，往往会得出一些与经济理论相反的结论.例如我们有时计算某厂的利润y、总产值x1、销售收入x2变化的二元线性回归方程

yc=-2094.57+05710x1-0.1429x2

(1)

(1)式表明，当工业总产值x1不变时，销售收入x2每增加一个单位，利润y平均减少0.1429个单位，显然与事实不符.导致这一问题的出现，主要是由于多重共线性的存在.事实上，这类问题在回归分析中并非鲜见.因此，有必要总结出多重共线性的检验及校正方法.

2 多重共线性的检验

通常多重共线性检验的方法有单相关系数矩阵法、t检验法和符合判断法.下面分别加以介绍：

(1)单相关系数矩阵法.所谓单相关系数矩阵法，就是分别计算出每两个自变量之间的单相关系数，并将计算结果列成一张矩阵表，在单相关系数矩阵中，任何两个自变量之间的相关系数r>0.8都可能导致多重共线性的出现，方法如下:

考察多元线性回归模型Y=β0+β1X1+…+βkXk,其解释变量之间的相关系数矩阵为:

因为rij=rji，所以上面相关阵为对称阵，rjj=1，只需考察主对角线元素上方(或下方)某个元素绝对值是否很大(一般在0.8以上)，就可以判断两个解释变量间是否存在多重共线性.另外需要特别注意的是，如果相关系数很大，则一定存在多重共线性，如果相关系数很小，不一定没有多重共线性.

如果欲建立某社会商品零售总额(当年实现的社会商品购买力)回归预测模型，初选三个自变量，依次是当年形成的社会商品购买力x1、上年末结合的购买力x2和当年零售商品货源x3.根据表1计算解得三元线性回归方程为

(2)

表2列出了自变量之间的单相关系数.从表2可以看出，自变量之间的单相关系数均大于0.8,处于高度状态，表明有多重共线性存在.

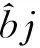
(3)

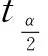
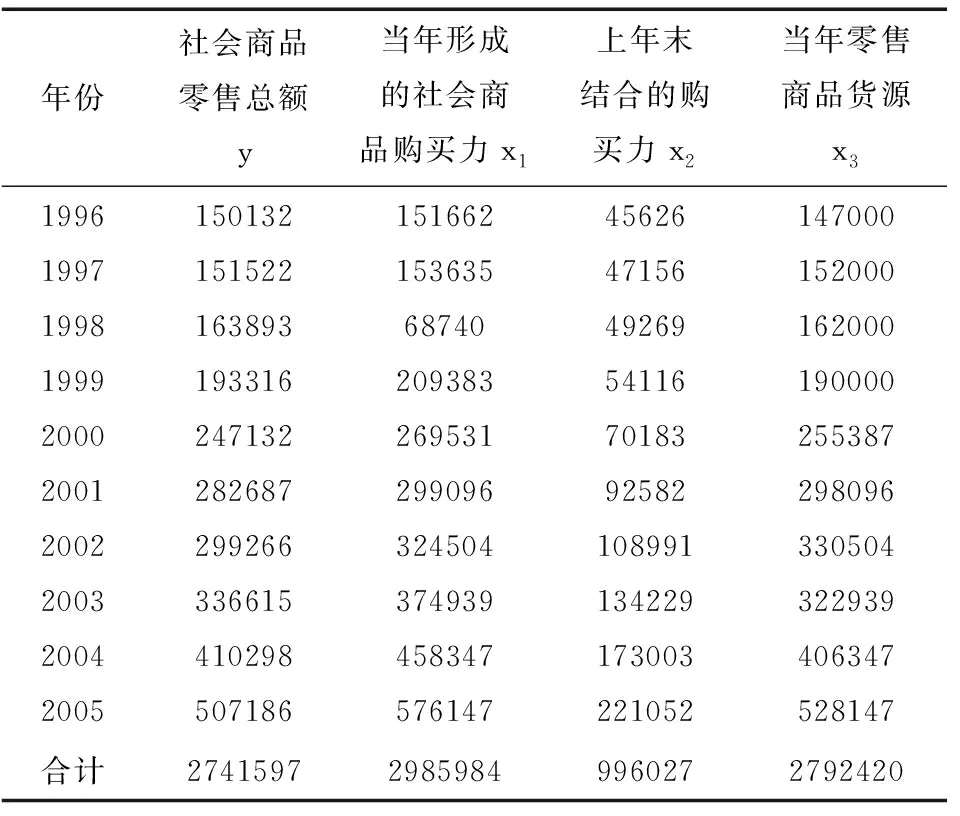
表1 某市社会商品零售总额预测基础数据表 (单位:百万元)

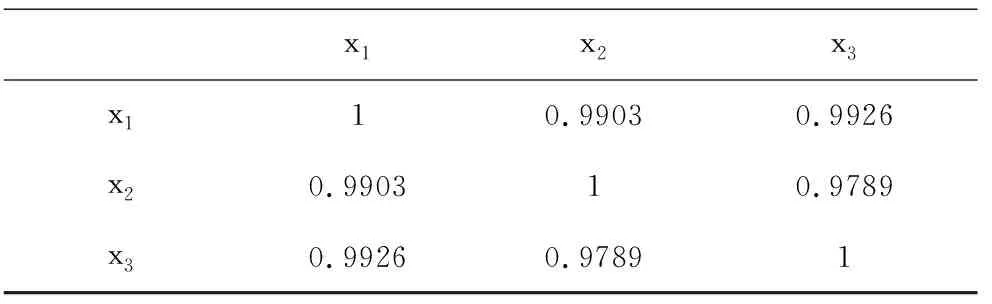
表2 单相关系数矩阵

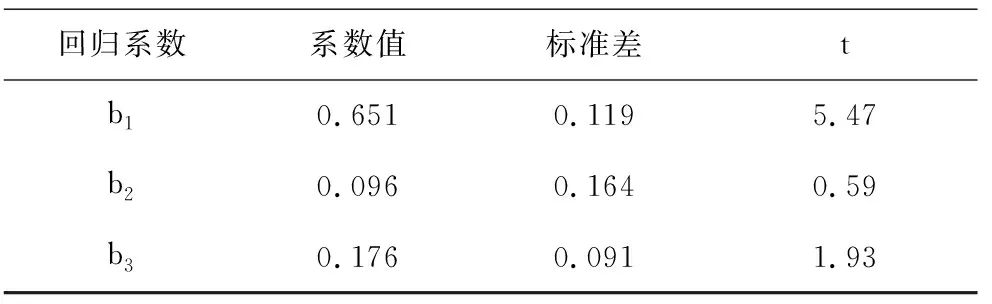
表3 回归方程的(2)的t检验

(3)符号判断法.如果回归方程中的回归系数b与其相应的单相关系数r正负号相反，表明有多重共线性存在，例如方程(1)的回归系数b=-0.1429,而工业总产值y与销售收入x之间的单相关系数r=0.68,正负号相反，因些我们断定方程(1)存在多重共线性.

以上阐述的三种检验方法，用于判断回归方程是否存在多重共线性，所起的作用是不同的，笔者认为单相关系数矩阵法可以作为查明多重共线性存在的必要条件；符号判断法可以作为查明多重共线性存在的充分条件；t检验法则应作为查明多重共线性存在的充分且必要条件.

3 多重共线性的校正方法

如果回归方程中存在多重线共线性，应设法消除或减轻它的影响.我们在解决方程(2)上多重线共线性的影响时，采用了删减变数和引入附加方程的校正方法，效果比较明显.现分述如下：

3.1 删减变数法

删减变数即删除多元回归方程中的某个自变量

(1)该自变量应该是与因变量之间相关系数最小者；

(2)在单相关系数矩阵中，应舍弃高度相关自变量中的一个；

(3)若某个自变量x的回归系数b与单相关系数r正负号相反，则应删除该变量.

根据以上原则并结合具体情况，我们删除了方程中(2)中的自变量x2x3，重新建立了社会商品购买力x的变化的一元回归方程：

yc=21367+0.8466xi

(4)

方程(4)的t检验结果见表4

表4 回归方程(4)的t检验

此时,t0=6.85、t1=89.12均大于t分布表中的t0.025=2.31的理论值.表明(4)式回归系数的显著性检验

3.2 引入附加方程法

结余购买力表现为沉淀的货币和银行存款，但是这部分在下一年内并非全部成为当年的购买力，其中一部分仍以结余的形式存在，因此我认为当年形成的社会商品购买力和上年末结余的购买力对社会商品零售总额的边际效应是有明显差异的，反映到回归方程(2)中，b1要大于b2，即

(5)

将上式代入(2)中，(2)式可化为

令

(6)

则有

(7)

至此，我们可以建立社会商品零售总额y依新变量Z、当年零售商品货源x3变化的二元回归方程.经计算：

yc=19819+0.6777Z+0.1689x3

(8)

4 多重线性对预测目标影响程度的定量分析

多重共线性无疑会给经济分析和预测带来误差，然而这种误差究竟有多大，目前在理论上还没有证实，这个问题可以通过对校正前后的回归方程进行“事后检验”，进而比较它们的预测误差来解决.例如前例某市的当年形成的社会商品购买力x1为698311百万元，当年零售商品货源x3为650000百万元，上年末结合的购买力x2为290013百万元，将上述数值分别代入方程(2)、(4)、(8)中求出当年社会商品零售总额的观测值，然后与实际值进行比较，计算出观测绝对误差和观测相对误差.有关计算结果见表5.

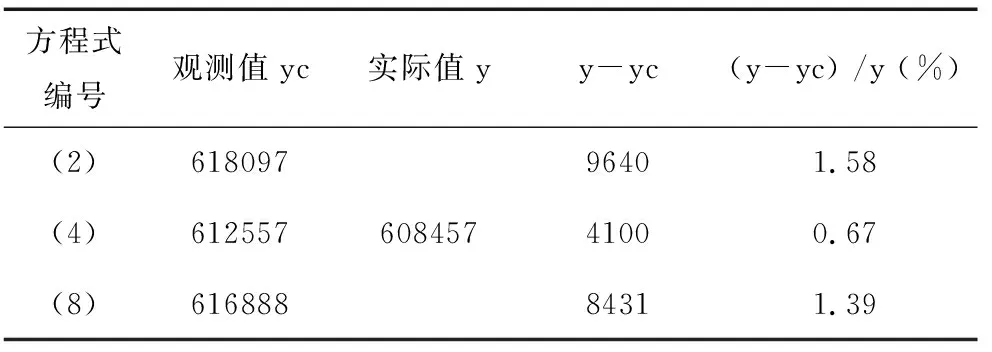
表5 预测绝对误差及预测相对误差计算表 单位:百万元

从表4可以看出，方程(2)的观测误差最大，方程(4)的观测误差最小.其中，从预测的绝对误差看，方程(2)比方程(4)大5540万元；从相对误差看，方程(2)比方程(4)高0.91%，这里的5540百万元和0.91%就是由于多重线性的存在对预测目标的影响程度.

多重共线性问题是计量经济分析中的重要内容，可以看出，多重线性的存在给多元回归分析和预测带来了一定的影响，但我们只要事先能够正确地识别它，并采取一定的补救措施，就会减轻或消除它的影响，从而使统计分析和观测建立在更加科学准确的基础上.

参考文献：

[1]盛骤.概率与数理统计[M].北京:高等教育出版社,2001.

[2][德]克劳斯 ·巴克毫斯.多元统计分析方法[M].上海:上海人民出版社,2000.

[3]李志伟.统计分析概论[M].北京:对外贸易出版社,1984.

[4]3克劳斯·巴克毫斯[德].多元统计分析方法[M].上海:上海人民出版社,2008.

[5]P.L.Meyer.[美].概率引论及统计应用[M].北京:高等教育出版社.1986.

[6]薛毅.最优化原理和方法[M].北京:北京工业大学出版社.2001.

[7]孙文瑜,徐成贤,朱德通.最优化方法[M].北京:高等教育出版社.2004.