大射电望远镜索牵引并联机构索力优化分析
黄 亮,朱文白,唐晓强,姚 蕊
(1.中国科学院国家天文台,北京 100012;2.清华大学精密仪器与机械学系,北京 100084)
上世纪90年代初,国际天文学界提出建造大型射电望远镜计划。经过不断努力,中国科学家提出利用贵州天然的喀斯特洼地,建造目前世界上最大的单口径射电望远镜——500m口径球面天文望远镜(Five-hundred-meter Aperture Spherical Telescope),简称FAST[1]。FAST望远镜馈源支撑系统主要有两级调节系统协调完成馈源的定位和指向调整:一级调节系统由6根钢索拖动馈源舱,实现馈源舱大范围的空间扫描,并初步满足观测要求;二级调节系统由AB轴、Stewart平台等部分组成,实现馈源精确定位和馈源姿态精整[2]。由高塔、钢索和馈源舱组成的一级调节系统可视为巨型索牵引并联机构。
索牵引并联机构自提出以来,凭借结构简单、工作空间大等特点,在起重、风动实验等诸多领域得到广泛应用[3]。为对索牵引并联机构实施控制,获得索长的准确信息是重要一环。很多索牵引并联机构索长跨度小,在分析中将绳索构型简化为直线。但在FAST望远镜中,钢索跨度超过100m,钢索的自重不能忽略,而呈悬链线状[4-5]。在悬链线方程中,钢索的索长和钢索的张力构成非线性关系,因此需要使用迭代法求解[5-6]。在有的机构中将悬链线简化为抛物线,通过引入Moore-Penrose广义逆来迭代求解[7]。
在应用迭代法求解索长的过程中,迭代计算开始前需要确定迭代初值,迭代初值的选取对收敛性和迭代步数有很大影响。而且每一步迭代都要求解一个线性方程组,解算效率较低。为提高解算效率,简化求解过程,本文提出一种线性简化模型——赝曲线模型。经过比较精确的非线性模型和简化模型的求解结果,说明了简化模型在求解上的精确性和快速性,为实时控制和大规模的计算提供便利。另外,由于馈源位姿调整由两级调节系统协作完成,在给定位置时,馈源舱体的姿态可在一定范围内变化,馈源舱可以在不同姿态下求解对应的索力和索长。故而在给定位置下,索力可视为姿态的函数。这就为索力的优化提供了可能。为此,本文还以在给定位置处6根钢索的索力值尽可能均匀分布为优化目标,对索力进行优化。
1 巨型索牵引并联机构
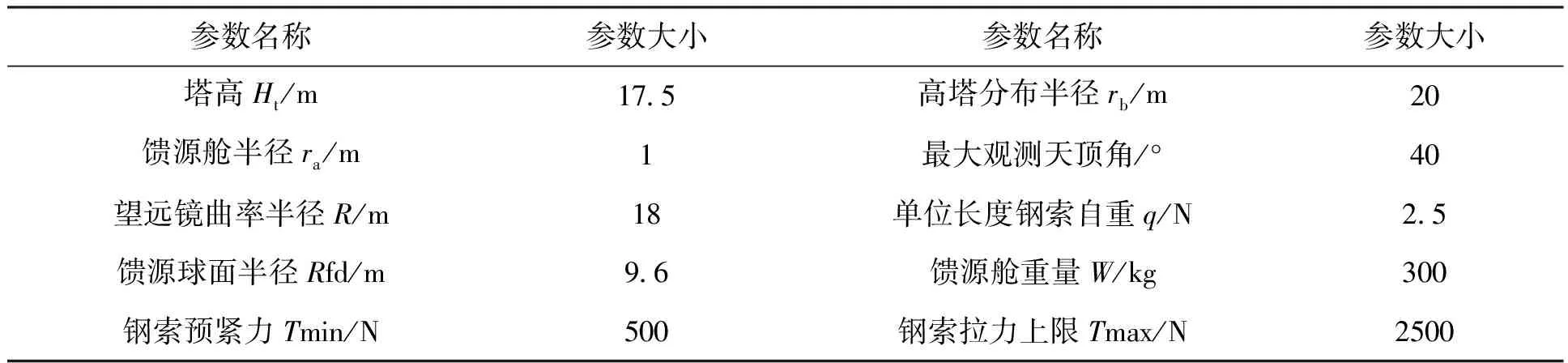
巨型柔索并联机构的基本结构如图1。6座高塔Ti(i=1~6)均匀分布在反射面周边,通过钢索牵引馈源舱在馈源球冠面上运动。馈源舱上有3个铰接点J1(J2)、J3(J4)、J5(J6),每个铰接点连接两根钢索,依次与高塔T1~T6对应。记与高塔Ti连接的钢索为Ci,i=1~6。馈源舱下安装AB轴与Stewart平台。在完成子系统关键技术实验后,中国科学院国家天文台在密云建造了机构完整的50m FAST缩尺模型,并在此基础上全面试验和验证FAST各项技术指标。
为便于描述,以反射面底部中心为原点O建立全局坐标系C1[X-Y-Z],X轴指向高塔T1,Z轴指向天顶。以馈源重心为原点Ow建立与馈源舱体固连的舱体坐标系C2[Xw-Yw-Zw],Zw轴与3个铰接点组成的平面J1J3J5垂直,指向天空方向;Xw轴垂直于Zw轴,指向铰接点J1。以钢索Ci与馈源舱体的铰接点Ji为原点OCi建立钢索坐标系C3i[XCi-YCi-ZCi],规定XCiOCiYCi平面与XOY平面平行,XCi轴指向对应的铁塔Ti,ZCi轴与Z轴方向一致,其中i=1~6,共有6个钢索坐标系。
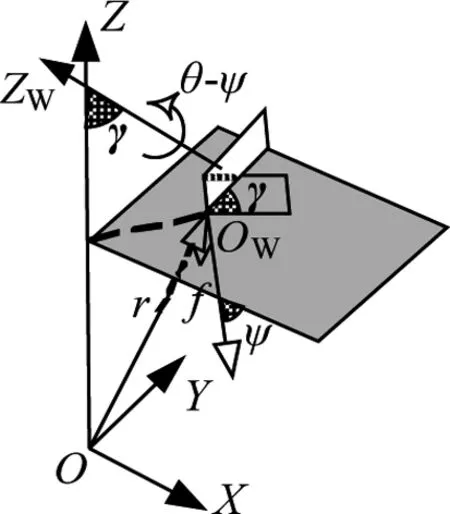
图2 舱体姿态角示意图Fig.2 Illustration of the attitude angle of the feed cabin
馈源舱的位姿可以通过全局坐标系C1到舱体坐标系C2的齐次坐标变换得到:在C1系中,先绕Z轴旋转角度θ,再绕单位向量f旋转角度γ,最后平移向量r得到C2系。其中单位向量f在C1系中表示为(cosψ,sinψ, 0),r=xwi+ywj+zwk,(xw,yw,zw)是Ow在C1系中的坐标,则变换矩阵可以写为:
Q=Trans(xw,yw,zw)Rot(f,γ)Rot(Z,θ)
(1)
其中Rot(f,γ)是绕f轴旋转角度γ的旋转矩阵[8]。
若向量f和向量r垂直,则角度γ即为舱体的倾斜角,舱体的姿态可以用(ψ,γ,θ)来表示。当舱体重心坐标(xw,yw,zw)给定,即可根据向量f垂直于向量r得到角度ψ。根据FAST望远镜机构的布局和坐标系的建立方法,角度θ不随舱体位置的变化而变化,始终为0.5236rad,即30°。
2 索力的解算和优化
2.1 钢索的受力分析
以某一根钢索为分析对象,省略下脚标i,记钢索与馈源舱的铰接点为B,钢索在B处所受拉力为TB,HB和VB分别为TB的水平和竖直分量;钢索与高塔定滑轮接触点为A,钢索在A处所受拉力为TA,HA和VA分别为TA的水平和竖直分量。钢索除在A、B两点受到拉力作用外,还要受自身重力作用,单位长度的钢索所受重力为q,其受力情况如图3。h和l分别为A、B两点之间的竖直和水平距离,σ为TB与水平面的夹角。

图3 钢索的受力分析Fig.3 Force analysis of a steel cable used as a catenary

图4 舱体的受力分析Fig.4 Force analysis of the feed cabin
钢索的形状可用不同的解析式来表达,为获得准确的索长信息,选用悬链线准确的表达式描述钢索形状:
(2)
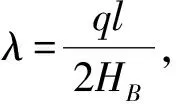
由(2)式可以得到钢索的索长L:
(3)
进一步代换可得:
(4)
对A点列写力矩平衡方程,可得到VB。记:
(5)
则钢索拉力的竖直分量为:
(6)
VA=qL-VB
(7)
作为柔性件,钢索不能承受压力,只能受拉力。为避免钢索虚牵,需给钢索一个最小的预紧力Tmin[3]。同时钢索的拉力不能无限增大,应小于拉力上限Tmax,故拉力应满足:
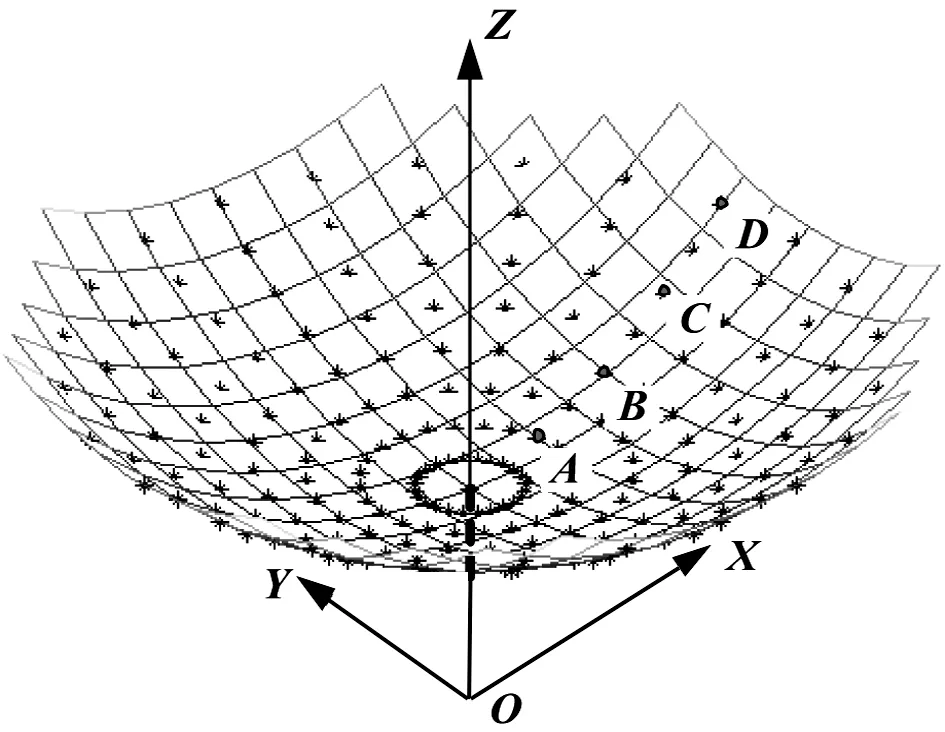
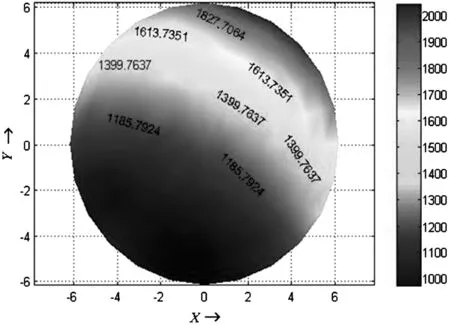
Tmin (8) 2.2.1 舱体静平衡方程 (9) 以HB为未知数,将(5)、(6)两式代入方程组(9),整理得: A6×6HB6×1=b6×1 (10) 其中: 式中ηi为第i个钢索坐标系的XC轴与全局坐标系X轴的夹角;(xJi,yJi,zJi)为第i根钢索与馈源舱铰接点在全局坐标系中的坐标; 式中W为馈源舱所受的重力;(xw,yw,zw)为馈源舱舱体坐标系原点Ow在全局坐标系中的坐标;I为式(5)所表达的积分项。待求的6根钢索索力水平分量组成列向量HB: HB=[HB1HB2HB3HB4HB5HB6]T. 由于方程组(9)是在精确的悬链线方程基础上得到的,因此称该模型为悬链线模型。由(5)式可知,积分项I为λ的非线性函数,因此方程组(9)为非线性方程组,要解出TB,需要使用迭代法。 为了得到迭代初始值,首先将悬链线简化为直线,有: (11) 对比(6)式,(11)式实际上是将(6)式中的积分项全部抛弃后剩下的部分,称这一简化模型为直线模型。由此可以将非线性方程组简化为线性方程组,整理得: (12) 其中A即为式(10)中的A项,b′=[0 0WWywWxw0]T。 当给定馈源舱位姿时,即可列写直线模型方程组(11),求解得到直线模型索力水平分量HBL。初值HBL确定后,就可用迭代法求解非线性方程组[6]。 求解悬链线模型须求解一个非线性方程组,应用迭代法将其转换为求解多个线性方程组。如果初值选的不好或停止条件过于苛刻,很可能导致结果不收敛或收敛很慢。在保证精度的前提下为简化计算,试图寻找其他线性模型作为悬链线模型的简化模型,即提出了赝曲线模型。 2.2.2 赝曲线模型及其求解 (13) 由(5)、(6)两式可知: (14) 对比(6)、(11)两式,(14)式并没有将(6)式中的积分项I全部抛弃,它考虑了钢索自重对A点的力矩作用,但是它认为力臂为l/2,没有考虑由于钢索形状的变化而导致钢索自重对A点力矩的变化。因此,它介于悬链线模型和直线模型之间,称之为赝曲线模型。利用简化结论(13)、(14),化简非线性方程组,可得: (15) 其中A即为式(10)中的A项。 式中Li为第i根钢索的索长,由式(14)求得。 当给定馈源舱位姿时,即可列写赝曲线模型方程组(15),求解得到赝曲线模型索力,记为TBS。解得的TBS需要满足式(8)所示的约束条件,若不满足则舍弃该解。求得满足条件的TBS,即可得到索长LBS。 根据天文观测的要求,馈源在跟踪射电源时,馈源的相位中心应该时刻位于射电源和反射面曲率中心所在的直线,即主光轴上,记馈源相位中心倾斜角的理论设定值为γ0。这一调节过程由两级调节系统共同完成:一级调节系统调节舱体的倾斜角γ,二级调节系统对馈源相位中心的倾斜角进行补充和精调。因此舱体的倾斜角γ可以在一定的范围内变化,只要一、二级调节系统的调节结果最终能够使馈源相位中心倾斜角达到γ0即可。也就是说在同一位置,馈源舱可以在不同的姿态下满足静平衡方程组。在某一位置(xw,yw,zw)和角度θ、ψ下,可以给定不同的γ值来求解出满足约束条件(8)的钢索索力,记使舱体同时满足(8)式和静平衡方程组的倾斜角γ的集合为Γ。索力TB即可视为倾斜角γ的函数。因此,可以选取一定的优化目标来对索力进行优化[9]。 当钢索牵引馈源到达某一位置时,如果6根钢索的索力差别很大,系统的力特性会变差,控制上表现出较大的时滞差异,难以协调[5,7]。为此提出以在给定位置处6根钢索的索力值尽可能均匀分布为优化目标,对索力进行优化。基于钢索索力方差最小原则的索力优化配置方法的寻找目标、目标函数、约束条件分别为: findγ∈Γ (16) s.t.AHB=b,Tmin 本文基于密云机构完整的50m FAST缩尺模型进行计算,其参数如表1。 表1 密云50mFAST缩尺模型参数Table 1 Parameters of the Miyun 50m scaled-down model of the FAST 为比较悬链线模型和赝曲线模型对索力的求解结果,选取馈源球冠面上的均匀分布的193个测试点进行计算。图5反映了这193个测试点在馈源球冠面上的分布。 图5 测试点在馈源球冠面上的分布Fig.5 The distribution of test points over the spherical cap for positioning the feed cabin 将赝曲线模型得到索力与索长分别记为TBS和LBS,悬连线模型解得的索力与索长分别记为TBC和LBC。两模型求解结果的比较见表2。 表2 悬链线模型与赝曲线模型求解结果的比较(i=1~6)Table 2 Comparison of the results between the Catenary Model and the Pseudo-Curve Model 从表2可以看出,两模型求解结果非常接近。利用精确的悬链线模型得到的结果,可以求得λch(λ)/sh(λ)在[1.000027, 1.001179]之间变动,sh(λ)/λ在[1.000013, 1.000590]之间变动,符合赝曲线模型简化条件,完全可以用赝曲线模型代替悬链线模型进行求解。在相同计算机硬件条件下,用C++分别编制赝曲线模型和悬链线模型索力求解程序,悬链线模型程序求解一个位姿下的索力平均耗时51.04μs,赝曲线模型程序耗时12.75μs,约为前者的1/4。在实时控制中会涉及到大规模计算,赝曲线的解算优势将在大规模计算中得到进一步体现,也为实时控制提供了可能。 当舱体倾斜角γ∈Γ时,各钢索均不虚牵。索力优化就是要在集合Γ中,选取一个γ满足优化准则。图6为沿X轴方向γ的取值范围。 图6 沿全局坐标系X轴倾斜角γ的取值范围Fig.6 Value range of γ(describing the inclination of the feed cabin) 图7 索力方差f(γ)随倾斜角γ的变化Fig.7 The change of f(γ)with γ,where f(γ) is the variance of the tension along a cable 利用(16)式对赝曲线模型解算的索力进行优化。选择馈源球冠面上的4个点A(0.8084, 0.2166, 8.4335),B(2.4007, 0.6433, 8.7242),C(3.9201, 1.0504, 9.2967)和D(5.3204, 1.4256, 10.1337),如图5。这4个点均匀分布在由馈源球冠面最低点到边缘的弧线上,具有一定代表性。通过索力优化,得到在不同倾斜角γ下这4点的索力的方差f(γ)曲线,如图7。 由图7可见,索力方差随着倾斜角的变化而变化;在某一倾斜角下,索力方差可取极小值,此时索力分布最为均匀。馈源舱越靠近馈源球冠面的边缘(如点D),索力方差的极小值越大,索力方差的变化幅度越大,索力方差对倾斜角变化越敏感,因此十分有必要对索力进行优化。 对馈源球冠面上的193个点进行索力优化,优化后的索力在[972.8N, 2101.8N]之间变动。对某一根钢索,索力随着索长的增大而减小;当索长较小时,索力对索长变化非常敏感,索长较大时,索力在1000N左右波动,变化不大。图8展示了第2根钢索的索力分布,钢索C2的索力TB2以高塔T2所在半径为对称轴对称分布,其他5根钢索的索力分布也具有类似特点。 图8 钢索C2的索力分布(N)Fig.8 The distribution of tension along the cable C2 给定位置下进行索力优化,同时也可得到与优化后索力对应的舱体倾斜角γ,利用式(4)也可得到钢索索长L。在赝曲线模型求解的基础上,表3给出了索力优化后FAST索牵引并联机构的有关参数值。 表3 索力优化后的计算结果Table 3 Calculations after the optimization of cable tensions 本文从大射电望远镜索牵引并联机构的静力学平衡方程入手,着力分析了静力学模型的建立和简化,并在此基础上对索力进行优化,得到一些有益结论,为后续工作奠定一定基础。 (1)在精确的悬链线模型基础上得到的赝曲线模型,将非线性方程组简化为线性方程组,赝曲线模型在保证求解精度的同时将求解速度提高了4倍,为实时控制或大规模仿真计算提供了便利。 (2)利用赝曲线模型得的满足约束条件的倾斜角组成集合Γ,γ在该集合内取值时都可以避免虚牵,为索力的优化提供了可能。提出以在给定位置处6根钢索的索力值尽可能均匀分布为优化目标,钢索索力方差最小为优化准则,对索力进行优化,得到满意的优化结果。优化后的索力是在该位置下分布最为均匀的一组。 致谢:在论文完成过程得到李辉等同事的大力帮助,提出许多宝贵建议,在此表示感谢。 [1] NAN Rendong.Five hundred meter aperture spherical radio telescope(FAST)[J]. Science in China: Series G Physics, Mechanics & Astronomy,2006,49(2):129-148. [2] 朱文白. FAST望远镜天文规划和馈源支撑的相关研究[D]. 北京:中国科学院国家天文台,2006,16-18,70-75. Zhu Wenbai. Researches on the kinematics planing and feed supporting design for FAST[D]. Beijing: National Astronomical Observatories, CAS, 2006, 16-18, 70-75. [3] 郑亚青,刘雄伟,林麒. 绳索牵引并联机构的研究概况与发展趋势[J]. 中国机械工程,2003,14(9):808-910. Zheng Yaqing, Liu Xiongwei, Lin Qi. Research Survey and Development Tendency of Wire-Driven Parallel Manipulators[J]. Chinese Mechanical Engineering, 2003,14(9): 808-910. [4] LI HUI, NAN RENDONG, KAERCHER H, et al. Working Space Analysis and Optimization of the Main Positioning System of FAST Cabin Suspension[C]//Proceedings of SPIE, Astronomical instrumentation, Ground-based and airborne telescopes Ⅱ,2008, Marseille,France.Bellingham: SPIE-International Society for Optical Engine,2008:70120T-1~70120T-11. [5] 孙欣,段宝岩. 巨型柔性Stewart平台解空间、工作空间的研究及悬索张力的优化分析[J]. 机械工程学报,2002,38(2):16-21. Sun Xin, Duan Boyan.Study on Solution Space,Working Space and Cable Tension’s Optimized Analysis for Huge Flexible Stewart Platform[J].Chinese Journal of Mechanical Engineering, 2002,38(2):16-21. [6] 杜敬利,段宝岩,仇原鹰,等. 舱索系统的非线性静力学分析与索长解算[J]. 机械科学与技术,2006,25(8):946-948. Du Jingli, Duan Baoyan, Qiu Yuanying,etal. Nonlinear Static Analysis and Cable-length Solution of a Cabin-cable System[J].Mechanical Science and Technology, 2006,25(8):946-948. [7] 姚蕊,唐晓强,李铁民,等. 大型射电望远镜馈源定位3T索牵引并联机构分析与设计[J]. 机械工程学报,2007,43(11):105-109. YA0 Rui,TANG Xiaoqiang,LI Tiemin,et al. Analysis and Design of 3T Cable-Driven Parallel Manipulator for the Feedback’s Orientation of the Large Radio Telescope[J].journal of Mechanical Engineering, 2007,43(11):105-109. [8] 谭民,徐德,侯增广,等. 先进机器人控制[M]. 北京:高等教育出版社,2007:34-36. [9] 王文利,孙欣,段宝岩,等. FAST中的宏/微机器人概念及索张力的优化配置[J]. 西安电子科技大学学报(自然科学版),2000,27(6):726-729. WANG Wen-li, SUN Xin, DUAN Bao-yan,et al. Concept of parallel matro/micro manipulator and optimal scheme for cable tension in the FAST project[J].Journal of XIDIAN University, 2000,27(6):726-729.2.2 钢索索力的求解

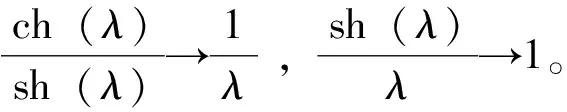
2.3 钢索索力的优化
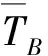
3 数值算例




4 结 论