基于CCD星图的空间目标精确光学定位方法研究

谌 钊，罗 成，华卫红

(国防科学技术大学光电科学与工程学院，长沙 410073)

空间目标主要是指人造卫星，包括工作的卫星和不工作的卫星，同时也包括各种空间碎片，如进入空间轨道的助推火箭、保护罩和其他物体，还包括进入地球外层空间的各种宇宙飞行物，如彗星和小行星。空间目标监测就是对这些空间目标进行探测跟踪、定位定轨预报、识别编目、侦察、分析等，而通过光学定位方法来确定空间目标的轨道则是实现空间目标监测的重要手段之一。光学定位方法是用天文望远镜和CCD探测器组成的光电摄像系统对空间目标进行成像，CCD便会将同一视场中的空间目标和其周围恒星同时记录下来，然后利用恒星的相关信息来确定空间目标位置的一种隐蔽、无源、被动的探测方法，该方法弥补了雷达探测易受到地面杂波和大气损耗的影响及自身功率和工作波长的限制而很难实现对远距离空间目标定位的不足，具有易于实现、成本低、精度高等优点。国外在空间目标光学定位领域已经做了大量的研究和实际应用，其中加拿大的CASTOR(Canadian Automated Small Telescope for Orbital Research)系统判读的卫星方位精度可达到2″。

本文提出一种基于CCD星图和球面几何原理且易于实现的空间目标精确光学定位方法。首先介绍一套用于获取CCD星图的小型空间目标精确光学定位系统，该系统获取的CCD星图中的空间运动目标轨迹的起点、终点时刻可精确到微秒量级，且系统成像过程满足线性成像的要求，以保证星角距的旋转不变性[1]。而后根据CCD星图的特点，提出Top-hat变换和中值滤波相结合的算法滤除星图中的噪声，包括光子噪声、背景噪声、仪器噪声和读出噪声以及CCD的颗粒噪声[2]。在此基础上，提出基于梯度Hough变换的星点、轨迹检测定位算法。与传统星点定位算法相比[3]，该算法运算速度快，能够实现对星点和空间运动目标轨迹的同时定位。最后利用星角距的旋转不变性和球面几何原理，实现对空间目标的精确定位，定位精度可达到角秒量级。

1 星图的获取

文中拍摄星图所用的小型空间目标光学定位系统主要由天文望远镜、CCD和GPS授时器组成。其中美国Meade公司的LX200R系列天文望远镜，口径为14英寸(356mm)；微光图像增强CCD(简称ICCD)，ICCD探测器的最大特点是灵敏度很高，响应时间在微秒量级，保证了能够得到精确的轨迹起止点的时刻。

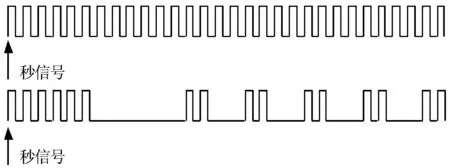
图1 控制ICCD分段曝光的方波信号Fig.1 Square wave signals for controlling the segmented exposures of the ICCD

如图1，GPS授时器提供一个卫星经过视场的整秒时刻，作为ICCD开始曝光的信号，称之为“秒信号”，并提供一个106Hz的TTL方波信号来控制ICCD进行曝光，这时得到的卫星轨迹将是一条连续密集的条纹线，轨迹的起点和终点时刻可以精确到微秒量级，但是却无法满足多个数据点(多段轨迹)的卫星定位要求。为此，编译单片机程序并制成实体控件与GPS授时器相连接，单片机程序可以将GPS授时器给出的106Hz的方波信号进行分段控制处理，用这样的方波信号再来控制ICCD的曝光，即可得到有多个可用数据点(多段轨迹)的卫星条纹轨迹星图。如图2，卫星经过视场时由望远镜系统工作在恒星跟踪模式下拍摄[4]，即望远镜跟踪恒星，CCD凝视天空中某一选定的位置来采集数据，则恒星呈现为光点，卫星由于运动而呈现为滑过视场的条纹轨迹。从星图中可以得到的信息有轨迹从长亮到长暗为卫星运动的方向；长短轨迹的长度比为3∶1(由单片机控件设定ICCD的曝光时间来调整)，且每段轨迹的起止时刻可精确计算到微秒量级。

图2 原始星图及其三维灰度分布图Fig.2 The original stellar image and the 3-D plot of its intensity distribution

2 星图预处理

CCD星图中的噪声主要是大量的背景灰度噪声，本文分3个步骤进行去噪处理，以达到对去噪效果的要求。

2.1 Top-hat变换

Top-hat变换是数学形态学中膨胀和腐蚀的组合运算。由膨胀和腐蚀这两种基本运算可以组合成开运算和闭运算。开运算是先进行腐蚀运算，再进行膨胀运算；闭运算则是先进行膨胀运算，再进行腐蚀运算。Top-hat变换是从原始图像中减去开运算后的图像来提取图像中小于结构元素尺寸的峰值，即亮特征。而星点亮度和背景灰度区别明显，选择大小合适的结构元素即可将大量的背景灰度去除。

2.2 中值滤波

中值滤波的原理是把序列中一点的值，用该点领域中各点值的中值来替代。在数字图像中采用一个含有奇数点的滑动窗口，将窗口中心点的值用窗口内各点的中值代替。其功能是使与周围像素灰度值的差比较大的像素用与周围灰度值接近的像素替换，从而可以消除孤立的噪声点。

2.3 二值化阈值分割

设原始图像为f(x，y)，采用双峰直方图方法[3]选取阈值T，将图像分割为两部分，分割后的图像为：

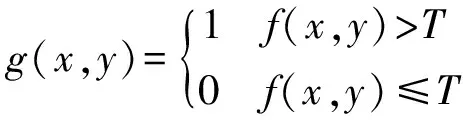
(1)

降噪后的星图如图3。

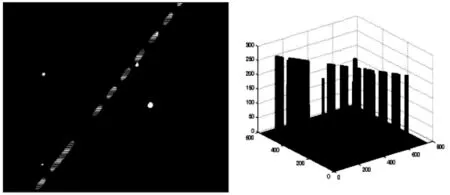
图3 降噪后的星图及其三维灰度分布图Fig.3 Stellar image with reduced noise and the 3-D plot of its intensity distribution

3 CCD星图星点和轨迹的精确定位

3.1 算法原理(圆Hough变换)

Hough变换所实现的是一种从图像空间到参数空间的映射关系，是图像处理中从图像中识别几何形状的基本方法之一，应用很广泛。

圆Hough变换的基本思想是，在(x,y)空间中圆的方程为：

(x-a)2+(y-b)2=r2

(2)

取(a,b)作为参数空间，因此在原图像(x,y)空间中圆上任意一点(xi,yi)与(a,b)空间中的圆：

(a-xi)2+(b-yi)2=r2

(3)

相对应。(x,y)空间中所有共圆的点，即满足(x-a0)2+(y-b0)2=r2的点，在(a,b)空间中的对应曲线相交于一点(a0,b0)。利用上述Hough变换的步骤，最终可在累加数组中寻找到(a0,b0)点出现的峰值，从而检测出在(x,y)空间中有一个以(a0,b0)为中心，r为半径的圆，即确定了CCD星图中星点的位置。本算法中的半径r可以自定义为某一个范围，用以检测实际所需的星点中心位置，减少了运算量，提高了星图处理速度。

3.2 梯度的求取

Hough变换星点定位算法首先要进行星点边缘检测，在数字图像处理领域中，一阶导数可以用于检测图像中的一个点是否是边缘点，而一阶导数是基于各种二维梯度的近似值的。图像f(x,y)的梯度定义为如下的向量:

(4)

梯度向量指向坐标(x,y)处f的最大变化率方向。在边缘检测中，一个重要的量就是这个向量的大小，用Δf表示：

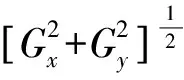
(5)

这是一个标量值，它给出了ΔF方向上每增加单位距离后f(x,y)值增大的最大变化率。梯度向量的方向也是一个重要的量。令θ(x,y)表示向量ΔF在(x,y)处的方向角，有：

(6)

这里角度是以坐标轴为基准度量的。至此，式(5)、(6)分别给出了梯度大小和梯度方向角的计算公式。两者都涉及到了Gx和Gy，也就是图像在每个像素位置上的偏导数∂f/∂x和∂f/∂y。有很多经典的边缘检测算子可以用来求Gx和Gy，如Roberts算子、Sobel算子和Prewitt算子等。这里将不再做详细论述。

3.3 算法的具体实现步骤

以极坐标方程形式来表示圆：

a=x-rcosθ,b=y-rsinθ

(7)

(7)式中，x和y为当前像素点的坐标；r为半径，其值可以事先指定或在一个循环中逐个取值，本算法是事先给出待检测星图中星点光斑半径的大概范围，然后循环取值；θ为求得的梯度方向角；a和b为计算得到的星点圆心坐标。利用梯度信息和圆Hough变换来完成星点、轨迹快速定位算法的具体实现步骤如下：

(1)扫描原始星图，利用梯度算子对其求梯度，并将梯度图像存放在新的缓冲区中；

(2)开辟一个二维的累加器缓冲区；

(3)扫描步骤(1)得到的梯度图像，将梯度值小于给定阈值的像素点排除在累加序列之外，而对梯度值等于或大于给定阈值的像素点，找到其在原始星图中的位置坐标x和y，用(6)式求其梯度方向角，设为θ，并在一个对半径r的循环中按(7)式求得星点的中心位置坐标a和b值，且对此累加数组进行累加操作。

(4)找到累加数组中值最大的那个元素，其对应的值就是所要检测的星点和轨迹的中心位置。定位结果如图4，图4中各星点和轨迹所对应的中心位置坐标如表1。

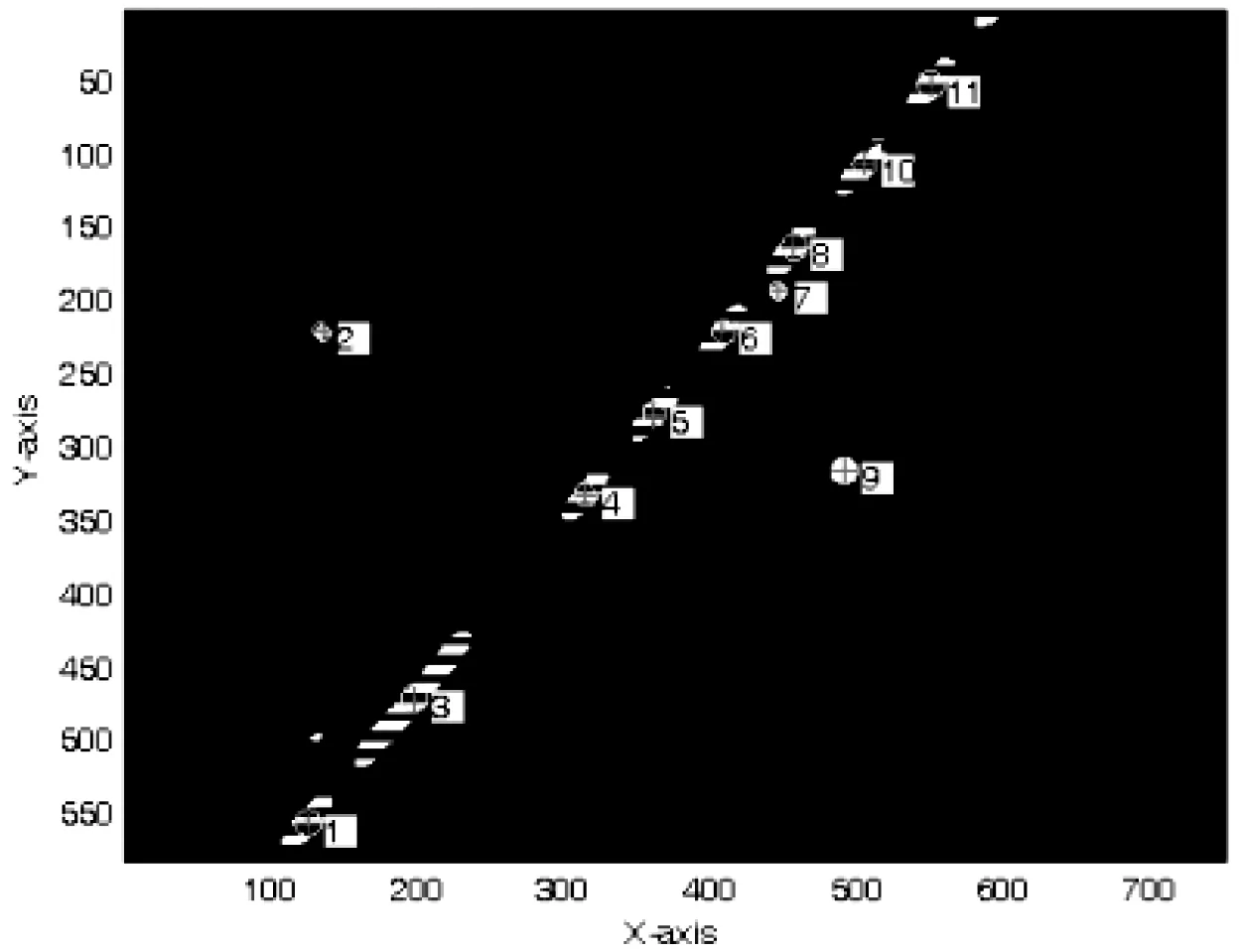
图4 星点、轨迹中心位置标记图像Fig.4 Image marked with central positions of stars and a track of object

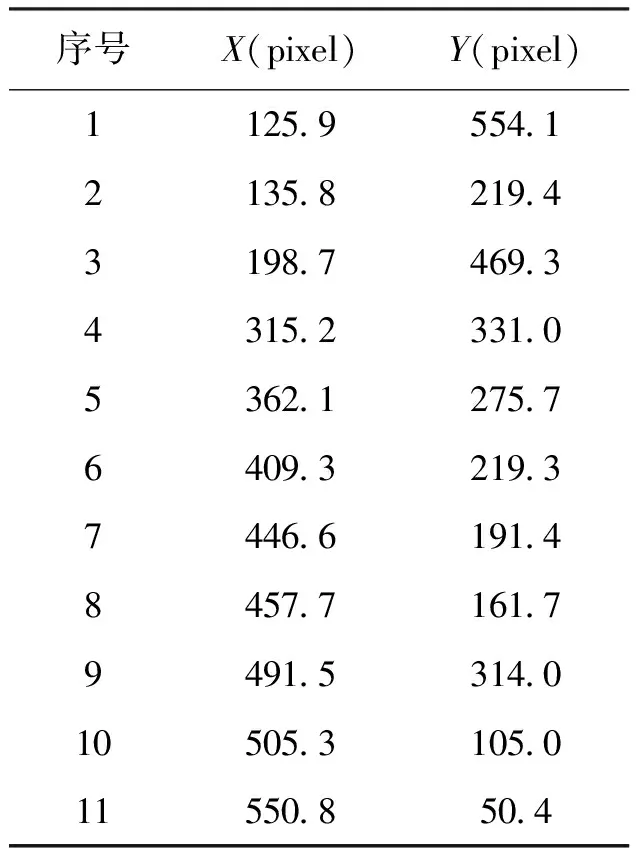
序号X(pixel)Y(pixel)1125955412135821943198746934315233105362127576409321937446619148457716179491531401050531050115508504

4 空间目标的精确定位

4.1.1 球面上两点的角距离公式(星角距)

如图5，dAB表示天球上两天体A(αA,δA)和B(αB，δB)的角距离，由边的余弦公式可得，球面上两点的角距离公式为:

cosdAB=cos(90°-δA)cos(90°-δB)+sin(90°-δA)sin(90°-δB)cos(αA-αB)

(8)

平面两点间的距离公式为：

(9)

图5 天球图Fig.5 Illustration of certain distanceson a celestial sphere

经过星图识别可得CCD星图中各恒星像点所对应的SkyMap星图软件中的恒星的详细星历信息，包括其赤经(α)和赤纬(δ)。利用(8)式和(9)式，可分别求出图4中所对应的各颗恒星间的角距离和CCD星图中两恒星像点间的距离。由于星角距的旋转不变性，可知恒星角距离和恒星像点间的距离一定对应成比例，即三颗恒星的角距离和其像点间的距离可构成一对相似三角形。以图4中的2、7、9号恒星为例，所构成的相似三角形的对应边的比值关系如表2。

表2 相似三角形对应边的比例关系

4.1.2 轨迹中心位置定位精度的检验

定义图4中数字序号3、4、5、6、8、10、11相邻两点之间的距离分别为L1、L2、L3、L4、L5、L6。原始星图中卫星条纹轨迹的长短变化是用单片机给出的TTL方波信号控制ICCD的曝光时间得到的，曝光时间之比为3∶1，经理论计算：

L1∶L2∶L3∶L4∶L5∶L6=2.5∶1∶1∶1∶1∶1

(10)

将表1中各点的位置坐标代入(9)式，得L1、L2、L3、L4、L5、L6值如表3。给出方差计算公式：

(11)

求得轨迹中心间距方差为S=1.7，即轨迹中心位置的定位误差最大为1.7个像素。此结果表明本文算法对轨迹中心位置的定位精度十分理想，完全可以用来求取运动目标的空间位置坐标。

表3 轨迹中心间距

4.2 两个已知恒星求解待测空间目标的位置

待测空间目标σ(α,δ)到两已知恒星(α1,δ1)和(α2,δ2)的角距离分别为d1、d2，则由(8)式可得：

(12)

求解(12)式中的方程组，即可得到待测空间目标的位置坐标。

4.3 空间目标定位精度的验证实验

选取图4中2、7、9号3恒星进行空间目标定位精度的验证。假设已知7号和9号恒星，2号恒星为待测空间目标。则可根据(8)式求得7号和9号恒星间的角距离，根据(9)式求得CCD星图中2、7、9号恒星像点间的距离。由表2结果可知，待测空间目标到两已知恒星间的角距离可由相似三角形边的比例关系来求取。将求取的角距离代入(12)式，再解算此方程组即可求得待测空间目标(2号恒星)的位置坐标。按上述方法对2、7、9号恒星进行交互式定位精度验证，并利用2、7、9号已知恒星两两求出3号轨迹处的空间位置坐标，结果如表4。

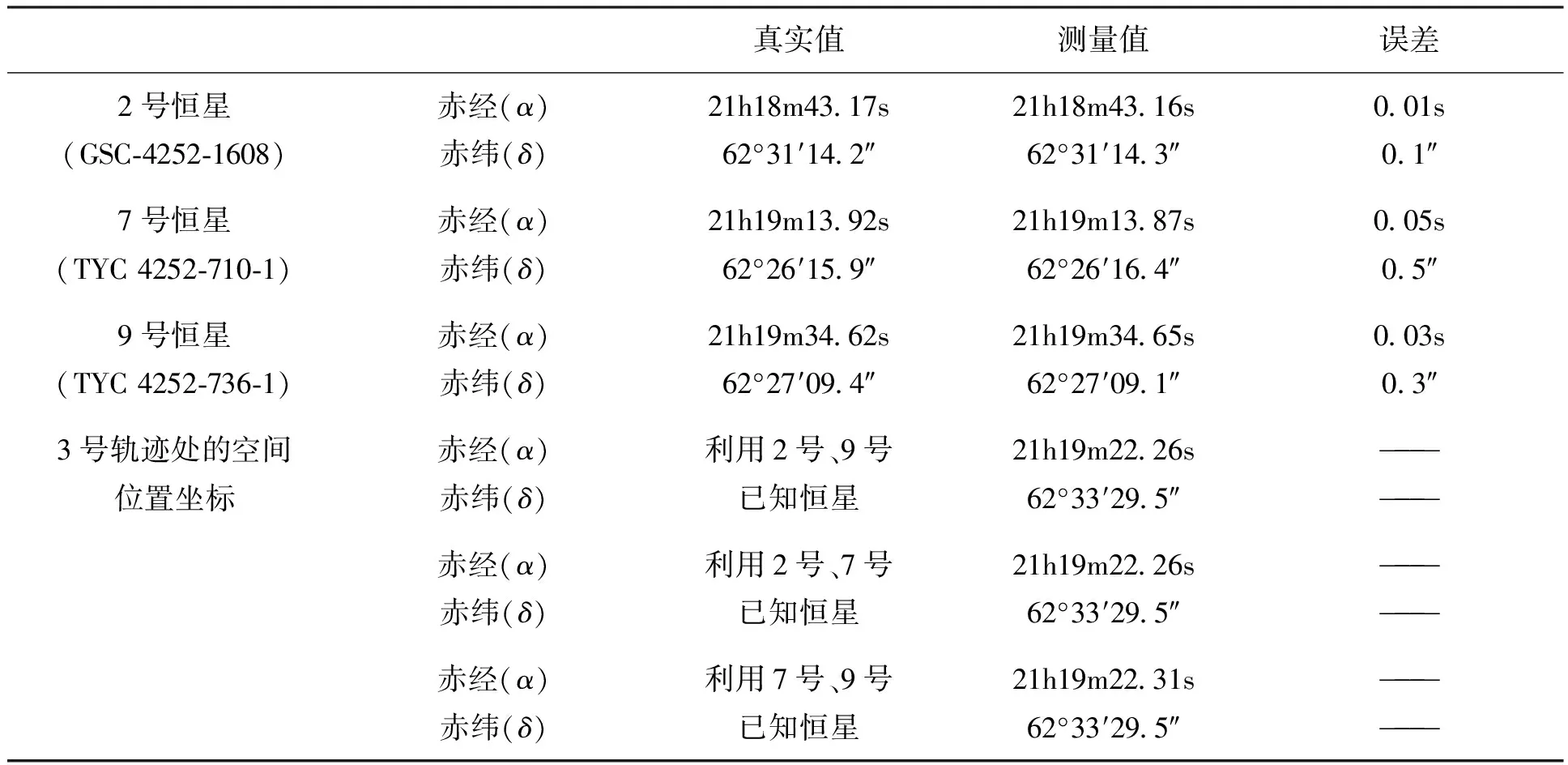
表4 空间目标定位精度验证实验结果

由表4的实验结果可以看出，本文方法对恒星空间位置的定位精度完全可以达到角秒量级，而对轨迹中心位置的定位精度也十分理想，所以用同样的方法来求取运动目标空间位置坐标的精度也必定能够达到角秒量级，并且用不同的两颗恒星来求取同一运动目标某一时刻的位置坐标的结果也基本保持一致。现在天文爱好者和天文科技工作者常用的电子星图软件SkyMap Pro 10对卫星位置的预报误差在5′～10′，其主要原因可能是建立预报模型时所考虑的影响因素不够全面，而且模型建立的时间也比较久远了。所以，本文方法在实际应用中也有很好的参考价值。另外，利用不同的恒星来给同一空间目标进行定位的结果不完全相同，本文将做进一步的研究，以便得到精度最高的空间目标定位结果。

5 结 论

本文利用一套小型的空间目标光学定位系统获取星图，基于ICCD极高的响应灵敏度，并通过单片机技术标定了星图中轨迹的起止时刻，其精度可达到微秒量级。用Top-hat变换和中值滤波相结合的算法滤除星图中的各种噪声；用基于梯度Hough变换算法完成了对星点和轨迹的同时精确定位，缩减了星图处理步骤；最后利用星角距的旋转不变性和球面几何原理，实现了对空间目标的精确定位，定位精度达到了角秒量级。这样一套简单的小型天文望远镜系统既能够实现对空间运动目标的精确定位，当条件满足时，还可用于卫星等空间目标的初轨计算[5]。所以，作为一种简单而有效的光学定位方法，其在空间目标监测领域必将有着广阔的应用前景。

[1] 李东明，金文敬，夏一飞，等.天体测量方法：历史、现状、和未来[M].北京：中国科学技术出版社，2006.

[2] 张春华，周晓东，陈维真.基于背景抑制的星空图像目标运动轨迹提取[J].红外与激光工程，2008，37(1)：143-146.

Zhang Chun-hua,Zhou Xiao-dong,Chen Wei-zhen.Target Trace Acquisition Method of Star Images Based on Background Elimination[J].Infrared and Laser Engineering,2008,37(1):143-146.

[3] 王兆魁，张育林.一种CCD星图星点快速定位算法[J].空间科学学报，2006，26(3)：209-214.

Wang Zhao-kui,Zhang Yu-lin.Algorithm for CCD Star Image Rapid Locating[J].Space Sci.,2006,26(3):209-214.

[4] 杨远贵，冯和生，郭锐，等.高轨空间碎片的观测模拟[J].天文研究与技术—国家天文台台刊，2004，1(1)：69-74.

Yang Yuan-gui,Feng He-sheng,Guo Rui,etal.The Observational Simulation of the Synchronous Debrises[J].Astronomical Reseauh & Technology,2004,1(1):69-74.

[5] 刘林，王海红，胡松杰.卫星定轨综述[J].飞行器测控学报，2005，24(2)：28-34.

Liu Lin,Wang Hai-hong,Hu Song-jie.Summary on Satellite Orbit Determination[J].Journal of Spacecraft TT&C Technology,2005,24(2):28-34.