边坡爆破振动传播规律的试验研究

钟冬望,陈江伟,余 刚

(1.武汉科技大学理学院,湖北武汉,430065;2.武汉科技大学冶金工业过程系统科学湖北省重点实验室,湖北武汉,430065)

随着国民经济建设的发展,爆破技术在采矿、水电、铁路、高速公路等基础建设项目中的运用越来越广泛,大规模的爆破开挖边坡的情况越来越多,但由爆破引起的边坡滑坡、坍塌等事故屡见不鲜。爆破对边坡的作用主要表现在两个方面[1-3]:一是形成的震动惯性力增加了边坡的致滑因素;二是爆破后出现不断的震动使边坡围岩中的剪应力增加,使原生结构面、构造结构面、原有的裂纹裂隙扩展和延伸,甚至产生新的爆破裂纹和微裂纹,致使其原有的力学性能下降,从而影响了边坡的整体稳定性。

边坡在爆破开挖过程中的稳定问题是一个亟待解决的问题。为了探索爆破震动的传播规律,寻求爆破荷载作用下边坡的动态响应及其响应与爆源之间的对应关系,陈士海等[4-7]研究了爆破开挖对边坡稳定性的影响,并通过现场监测提出了切实可行的减震措施。为此,本文从爆破地震效应分析入手,对实验室内混凝土边坡的爆破振动进行试验研究,探讨爆破振动在边坡中的传播规律,并分析了边坡爆破振动对边坡作用机理和地震强度的影响,以期为了解边坡爆破振动对边坡地震强度的变化规律提供试验依据。

1 试验

1.1 模型的制作与安装

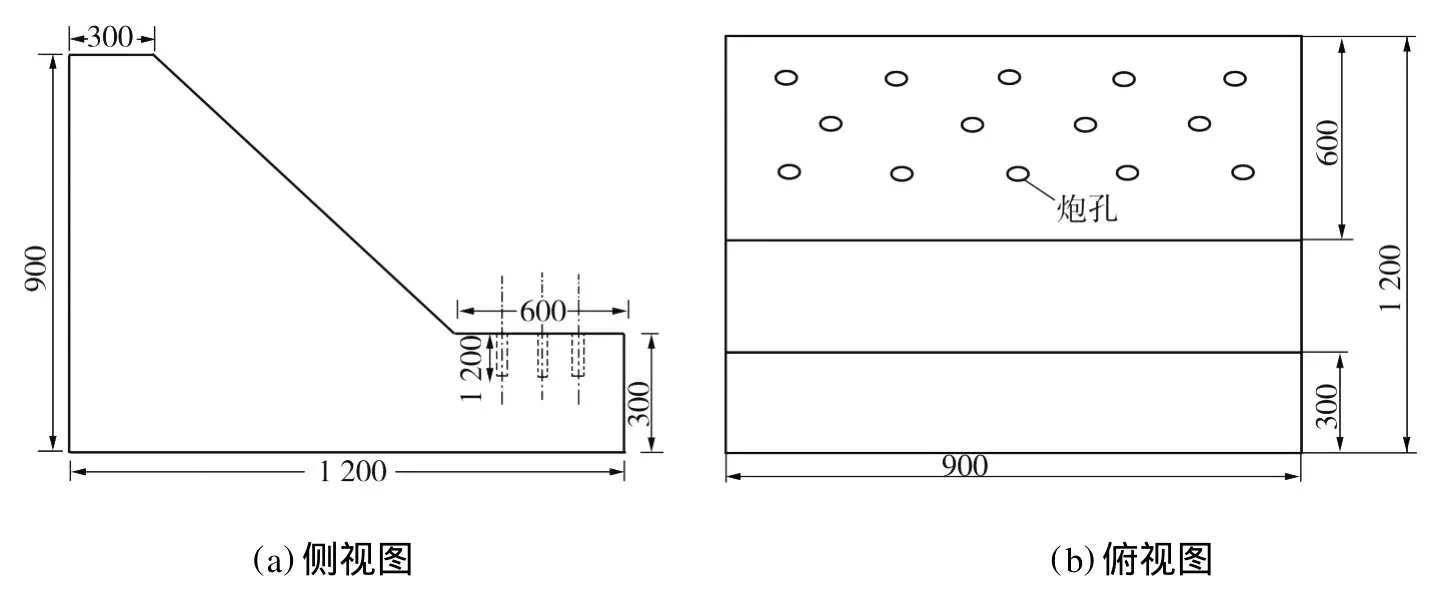
图1 试件模型的侧视和俯视图(单位:mm)Fig.1 Side and top view of the specimen model

图1为试件模型的侧视和俯视图。模板按图纸的尺寸进行加工,模拟试件的制作由425#硅酸盐水泥和筛选后的细砂浇注而成,配比为m(水)∶m(水泥)∶m(砂子)=0.5∶1∶2,养护28 d。图2为试件的实际模型。成型试件模型的主要参数如下:压缩强度为42.5 M Pa;体积密度为2 436 kg/m3;泊松比为0.20;拉伸强度为2.53 M Pa;弹性模量为33.4 GPa;纵波速度为4 052 m/s;模型边坡角为42°。试件规格为1 200 mm×900 mm×900 mm,共分2组:一组在离底线100 mm处设有深为250 mm、宽为10 mm预留的预裂缝,另一组未设。每个模型台阶上预留14个炮孔,炮孔的排距为100 mm,孔距为200 mm,炮孔直径为10 mm,炮孔深度为200 mm,孔内采用8#纸质普通瞬发电雷管。为保证炮孔堵塞效果,除预留装药长度外,其余全部用细沙堵塞。由于试件模型尺寸较小,为了减少和消除试件模型四周自由面对爆破效果的影响,爆破前还在垂直爆破自由面方向的两侧施加钢板,并用钢筋和螺栓夹紧,以便模拟边界效应。

图2 试件实际模型图Fig.2 Actual specimen model

1.2 测试系统和测点布置

本试验所用测试仪器为IDTS3850爆破振动记录仪。该爆破振动记录仪可同时记录3个方向的振动速度,其分辨率高,最小分辨振动速度可达0.001 6 cm/s,读数精度达到0.5%,并可自动地实时采集8次爆破振动波形。在坡顶等间距分别布置3个测点,在坡身正中间布置1个测点,在坡底与坡身交界处布置3个测点,共计7个测点。每个测点布置1台爆破振动记录仪和1台水平垂直2个方向速度传感器。速度传感器的安装是在设计点位钻凿一直径为6 mm、深为50 mm的孔,将传感器的尖锥插入并固定,保持与试件耦合即可。图3为试件模型的俯视平面图。

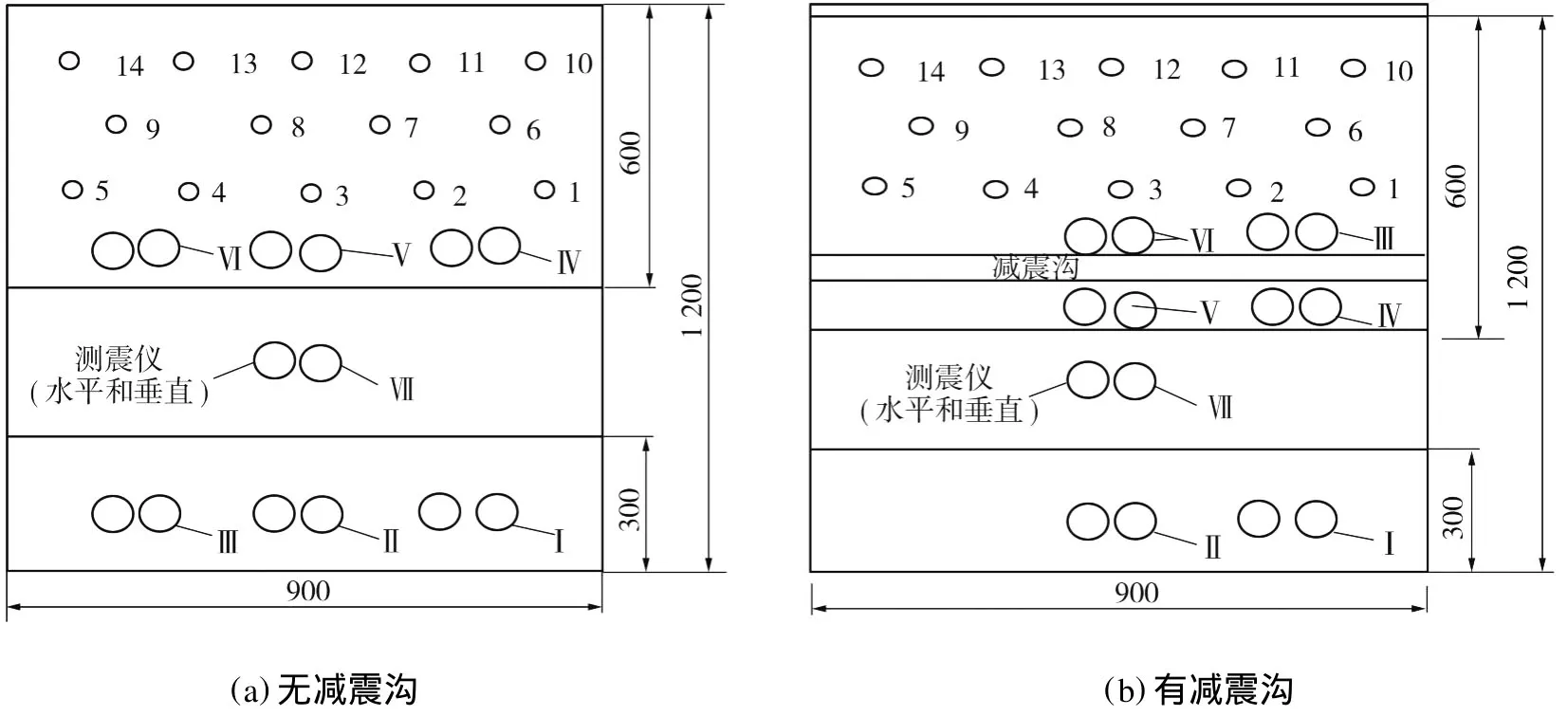
图3 试件模型的俯视平面图(单位:mm)Fig.3 Planar graph of the specimen model

2 结果与分析

2.1 试件爆破振动分析

爆破地震波的破坏作用主要决定于质点振动速度,而不是波自身的传播速度,其传播和衰减遵循一定的规律。因此,只要估计质点的最大振动速度并采取一定的控制手段,就可减少爆破振动带来的危害。质点的最大振动速度公式为

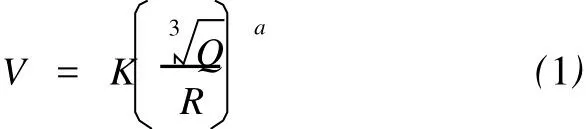
式中:V为质点振动速度,cm/s;Q为单段最大药量,kg;R为爆破中心至被保护对象或测点的距离,m;a为爆破地震波传递的衰减指数;K为爆破现场地质条件的系数。

对预裂缝减振的效果可直接采用计算法、推算法、频响分析法和动力学计算法等[8]。采用推算法,即首先在与现场实际相似的台阶模型上测得大量爆破振动数据,再根据测点与不同爆源的距离采用

式中:ri为测点至第i爆源的距离,m;qi为测点至第i爆源的药量,kg。式(2)～式(4)求等效距离R—、等效药量Q—和相应的比例距离r—;最后再对振动速度和比例距离取对数,通过回归分析后,得出预裂缝振动衰减公式。

2.2 试件爆破振动传播规律的分析

在无减震沟的情况下,先对每个孔使用单发8#瞬发电雷管,然后逐个孔进行爆破,并对不同炮孔爆破时同一测点的振动速度进行分析。表1为起爆孔点爆破时测点1监测的振动速度。由表1可看出,在同一个测点上,距离爆源越远振动速度越慢,地震波随着距离的延长呈衰减的趋势,但垂直方向振动速度的衰减速度明显大于水平方向振动速度的衰减速度。

表1 起爆孔点爆破时测点1检测的振动速度Table 1 Vibration velocity of first monitoring point after blasting

再对某一炮孔爆破后不同测点的振动速度进行分析。表2为孔点10起爆后6个监测点的振动速度。图4为表2所列数据制作的振动速度衰减图。由图4可看出,当炮孔起爆后,距离爆源越远,振动速度越慢,地震波随着距离的延长呈衰减的趋势,但垂直方向振动速度的衰减速度明显大于水平方向振动速度的衰减速度,这与振动传播理论相吻合。

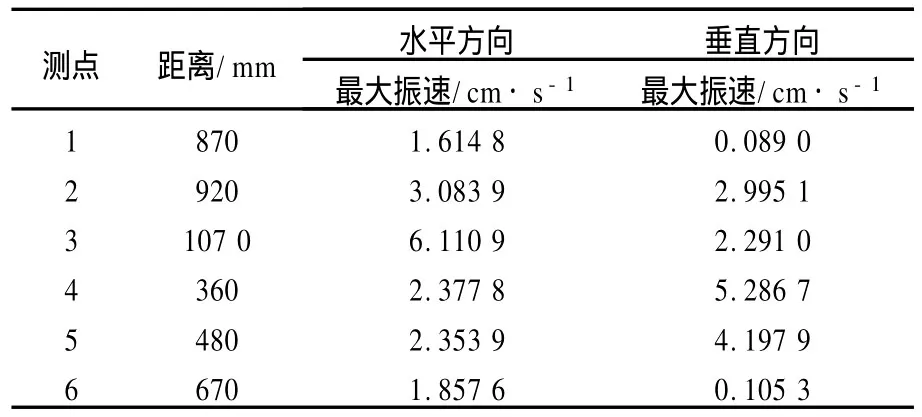
表2 孔点10爆破时各测点监测的振动速度Table 2 Vibration velocity of each monitoring point after blasting

图4 振动速度随距离的变化Fig.4 Variation of vibration velocity with the distance

由于工程实践中通常用垂直方向的最大振动速度作为判据,因此根据所测得的数据用Sadovsk公式进行回归分析,即可得振动速度衰减公式。对坡顶测点垂直方向的振动速度回归后,得:K1=153.62,a1=1.77;对坡底测点垂直方向的振动速度回归后,得:K2=104.87,a2=2.28。由此可得试件模型的振动速度衰减公式,即:

式中:V坡顶为坡顶测点质点振动速度,cm/s;V坡底为坡底测点质点振动速度,cm/s;Q为单段最大药量,kg;R为爆源至测点的水平距离,m。

比较式(5)、式(6)后发现,在同样条件下坡顶振动速度大于坡底振动速度,具有明显的高程放大效应;其次在同样条件下坡顶振动速度的衰减速度明显小于坡底振动速度的衰减速度,表明在临近边坡爆破时,边坡具有放大振动速度的作用,且振动速度的衰减速度变慢。

2.3 试件预裂缝减振效果分析

在试件模型中,坡底距离坡面100 mm的断面处有一个深为250 mm的减震沟,其平面图如图3(b)所示。为了便于分析,分别在预裂缝两侧设2组对称测点(测点3与测点4,测点5与测点6),其中处于预裂缝爆破区一边的有测点3和测点6,处于预裂缝保护区一边的有测点4和测点5,距离预裂缝均为50 mm。表3为孔点14用单个8#瞬发电雷管起爆后7个测点的振动峰值。据此分别将预裂缝两侧对称测点(测点3与测点4,测点5与测点6)的垂直方向振动速度和水平方向振动速度制作对比直方图,如图5所示。由图5(a)可看出,将爆破区测点3与保护区测点4的振动峰值作比较,其水平方向振动峰值降低了67.9%,垂直方向振动峰值降低了72.7%。同样地,由图5(b)可看出,将爆破区测点6与保护区测点5的振动峰值作比较,其水平方向振动峰值降低了64.7%,垂直方向振动峰值降低了86.2%,表明试件模型中的减震沟可将水平方向振动峰值降至64.7%～67.9%,垂直方向振动峰值降至72.7%～86.2%。分析结果表明,人工预留的预裂缝作为减震沟有明显的减震效果。

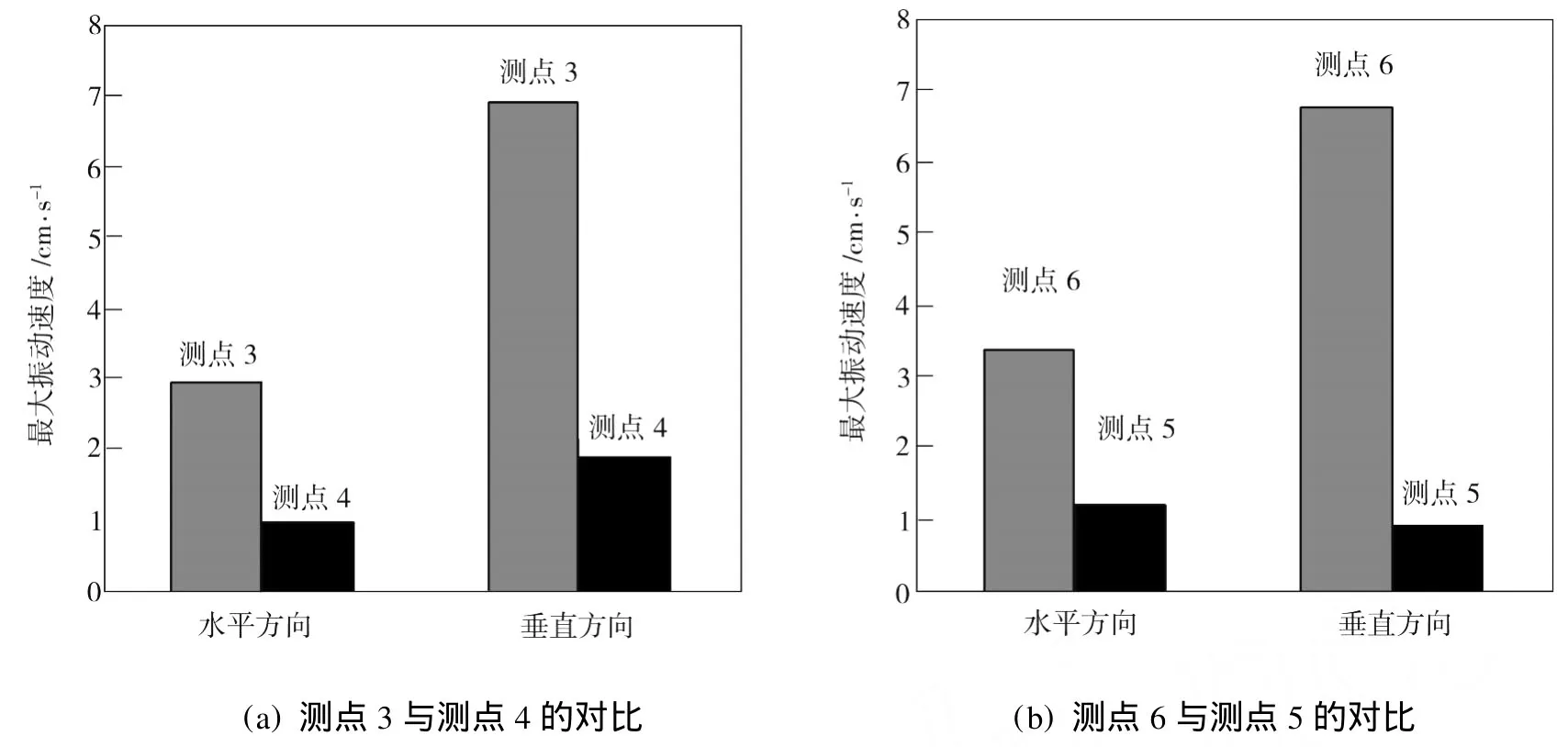
图5 预裂缝的减震效果示意图Fig.5 Schematic diagram of dam ping effect on the pre-split crack

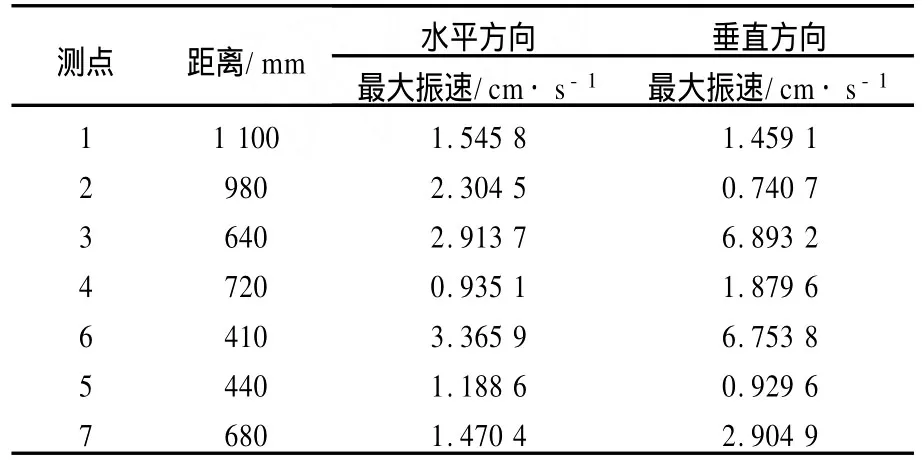
表3 孔点14爆破时各测点监测的振动速度Table 3 Vibration velocity of each monitoring point after blasting

3 结论

(1)试验条件下,混凝土试件模型的振动速度衰减公式分别为V坡顶=153.62(Q1/3/R)1.77;V坡底=104.87(Q1/3/R)2.28。

(2)距离爆源越远,振动速度越慢,地震波随着距离的延长呈衰减的趋势,且垂直方向振动速度的衰减速度明显大于水平方向振动速度的衰减速度。

(3)在同样条件下,坡顶振动速度大于坡底振动速度,具有明显的高程放大效应,且坡顶振动速度的衰减速度明显小于坡底振动速度的衰减速度,表明临近边坡爆破时,边坡具有振动速度放大作用,且振动速度的衰减速度变慢。

(4)试件模型中的减震沟可将水平方向振动峰值降至64.7%～67.9%,垂直方向降至72.7%～86.2%,表明预裂缝具有明显的减震效果,可运用于实际的边坡爆破工程。

[1] 李祥龙,庙延钢,杨溢,等.爆破震动对边坡稳定性影响分析[J].爆破,2006,23(4):15-19.

[2] 李廷春,沙小虎,邹强.爆破作用下高边坡的地震效应及控爆减振方法研究[J].爆破,2005,22(1):1-6.

[3] 李海波,蒋会军.动荷载作用下岩体工程安全的几个问题[J].岩石力学与工程学报,2003,22(11):1 887-1 890.

[4] 陈士海.爆破地震动研究现状[J].爆破,2003,20(1):13-18.

[5] 严晓新,李玉河.爆破动力对岩石边坡稳定性影响[J].隧道建设,2003,23(6):15-30.

[6] 舒大强,何蕴龙.岩质高边坡开挖爆破震动载荷及其对边坡稳定性影响的研究[J].工程爆破,1996,2(4):4-7.

[7] 贾虎.爆破动载作用下邻近硐室围岩稳定性的研究[D].淮南:安徽理工大学,2006.

[8] 钟冬望,林大泽,肖绍青.爆炸安全技术[M].武汉:武汉工业大学出版社,1992:24-56.