路基不均匀沉降值对板式轨道动力响应的影响

周 萌,宫全美,王炳龙,周顺华

(同济大学道路与交通工程重点实验室,上海 200092)

高速铁路为铁路事业的发展带来了新的机遇,其安全、可靠、舒适取决于构成铁路系统各方面的高品质和高可靠性。板式轨道在铁路中的应用始于1965年日本新干线,具有轨道平顺性高、刚度均匀性好、轨道几何形位能持久保持、维修工作量较少等特点,在各国高速铁路中得到了广泛应用,并对其开展了必要的研究工作。对于行车的安全性和轨道动力特性，一般建立车辆-轨道耦合模型进行求解,而对于轨道结构的受力分析则多以静载进行分析[1]。文献[2]通过建立车辆-轨道耦合模型对路基不均匀沉降下的板式轨道进行动力性能评估,按照客车舒适度的要求提出路基的不均匀沉降应控制在20 mm/20 m以下。文献[3～4]根据规范的设计轮重通过静力分析对轨道结构的强度做了一定的研究。但动荷载作用下的轨道结构动力响应和动载下轨道板的强度问题依然缺乏研究。路基工后沉降导致的轨道结构破坏是影响行车安全的主要因素。由于土质路基上铺设无砟轨道在我国尚处于起步阶段,对于无砟轨道线路在列车荷载长期作用下的轨道结构振动特性、变形特性以及运用安全性等方面都缺乏足够的理论、试验研究和设计经验。

本文将移动荷载和轨道-路基模型作为一个系统,分析了不同路基沉降量对板式轨道的动力影响,并对轨道的混凝土构件进行了强度校核。

1 板式轨道有限元分析模型

1.1 运动方程的求解

根据虚位移原理,有阻尼作用的连续弹性介质经有限元离散为多自由度体系后,整体的动力平衡方程为

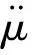
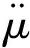
对运动方程的求解采用Newmark隐式直接积分法,根据给定初始时刻的位移、速度和加速度后,在t+Δt时刻的响应值应满足动力平衡方程(1),可求得t1时刻的位移、速度和加速度。而后逐步求得t1…tn时刻的解。

1.2 列车荷载的模拟

本文通过移动荷载对列车荷载进行模拟,文献[5]总结了荷载动力系数的取值研究。法国TGV高速列车最大计算轮重采用137 kN,德国ICE高速列车采用174 kN作为计算轮重,分别为静轮重的1.61倍和1.73倍。日本对轨道结构进行疲劳检算时,动力系数根据东海道新干线的实测值,取φ=1.45。

国内秦沈客运专线试验结果：无砟轨道试验速度达到321 km/h时,长枕埋入式无砟轨道动力系数为1.94,板式无砟轨道动力系数最大为1.57。我国在经过5次提速后,通过对测试数据的分析,国内学者建议,在速度≥200 km/h线路上,客运专线动力系数为2，客货共线动力系数为3。

车辆在通过路基正余弦不均匀沉降区域时,轮轨力会增大,且出现近似正余弦的波动,文献[6]计算了20 m波长下不同路基沉降量对轮轨力的影响,沉降幅值为10、20、30 mm时，300 km/h的客车轮轨力峰值分别为86、93、100 kN。鉴于增幅并不是很大,因此本文在计算时对0～30 mm的路基沉降量荷载幅值皆采用2倍的静轮重,速度为300 km/h,易比较沉降量的影响。

通过4对移动荷载模拟相邻转向架的经过，在任一时刻t,设车辆匀速移动轮载为

f(t)=K×p×δ(x-vt)(2)

式中K——动力系数,取值为2；

p——静轮重,取值为75 kN；

x——轮载在t时刻的位置；

δ——δ函数,即δ(xi=vti)=1,δ(xi≠vti)=0,xi为轨道板上承轨槽所在位置,xi=x0+ils(i=1,2，…),x0为初始参考点,ls为承轨槽间距。取转向架轴距为2.4 m,转向架中心距为18 m,车速v=300 km/h,经过两相邻承轨槽所需的时间Δt=ls/v。

1.3 路基不均匀沉降的模拟

假设路基表层的不均匀沉降形式为全波长余弦不均匀沉降,表达式为

(3)

余弦的弦长为20 m,绝大多数的路基不均匀沉降采用非线性弹簧进行模拟,本文根据点的几何坐标拟合余弦沉降曲线,并在路基上表面和混凝土底座的底面设立接触面,建立起轨道—路基三维有限元模型(图1),分析荷载经过时混凝土底座与路基面的接触状况,更贴近实际情况。接触面采用ADINA软件中的不穿透接触,即假设接触面在垂向为刚性的。路基的横截面为梯形,坡度为1∶1.5,采用线弹性的8节点实体单元,轨道板和混凝土底座在路基上的排列形式如图1所示,并对其进行1-3的编号。

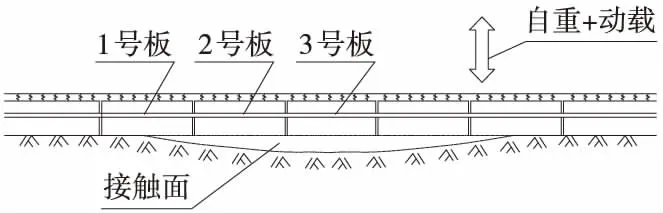
图1 路基不均匀沉降下轨道结构模型简图

1.4 板式轨道结构的力学模型参数

土质路基上的板式轨道主要是由钢轨、扣件和胶垫、轨道板、CA砂浆、混凝土底座、基床等组成,各构件的尺寸和参数如表1所示。

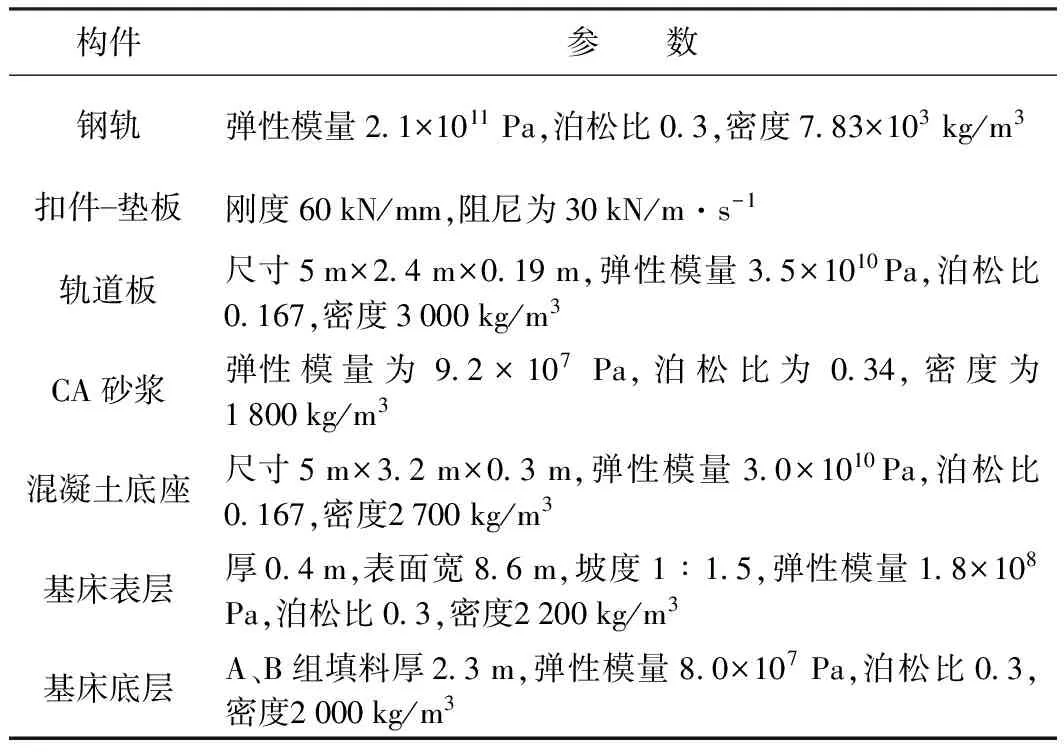
表1 土质路基上板式无砟轨道结构计算参数

模型建立时,将钢轨视为连续弹性点支承基础上的两节点哈密顿梁,轨下胶垫系统和扣件视为弹簧—阻尼结构,弹簧的初始长度为38 mm,一端与钢轨连接,一端与轨道板连接,弹簧的刚度为60 kN/mm,阻尼为30 kN/m·s-1,轨道板、CA砂浆、混凝土底座采用线弹性的8节点实体单元,3种结构层之间不考虑相互的错动,采用连续耦合相互作用,根据《客运专线无砟轨道铁路设计指南》等规定要求,混凝土底座结合轨道板每5 m设置1道伸缩缝,与轨道板采用对缝布置的形式。

2 板式轨道计算结果分析

2.1 路基不均匀沉降对轨道板的影响

路基是轨道结构的基础,路基的沉降特别是不均匀沉降会直接对轨道结构产生影响。路基的工后不均匀沉降使轨道结构产生的变形附加应力,轻者可导致轨道结构服务性能下降,对列车的舒适性产生影响；重者可能导致轨道结构损坏,影响行车的安全。

通过轨道-路基耦合模型的计算分析,将移动荷载作用下的轨道板各向应力、动位移幅值列于表2中,以对比不同的路基沉降量对轨道板的力学影响。

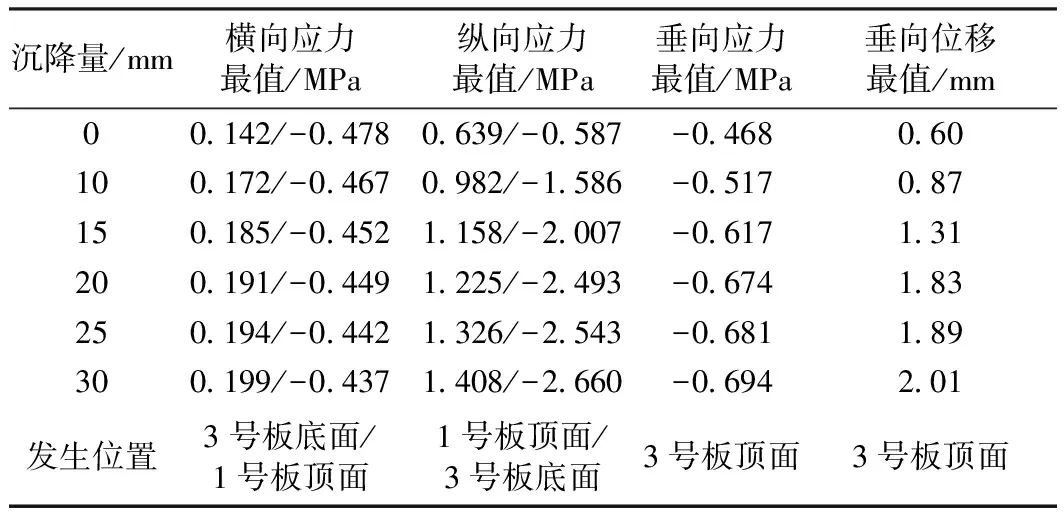
表2 不同路基沉降量对轨道板的影响

注：拉应力为正,压应力为负。

(1)路基沉降对横、纵向应力的影响

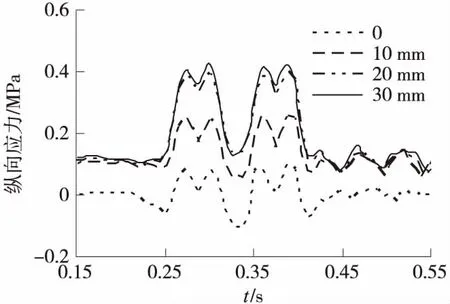
图2 不同沉降下轨道板底面节点纵向应力随时间的变化曲线

图2为3号轨道板底面轨下位置中间节点的纵向应力随时间的变化曲线。当荷载经过时,随着路基沉降量的增大,该节点的纵向应力在沉降量为20 mm前增长明显,沉降每增加10 mm,纵向应力增加1倍。在相同的荷载幅值下,沉降量超过20 mm后应力增长缓慢。但并非说路基沉降量可以很大,若沉降量较大轮轨力也会增加较大,且不会满足列车舒适度要求。

当一个转向架荷载行至3号轨道板中间时,3号轨道板底面轨下位置的横、纵向应力随位置(板长方向)的变化如图3所示。结合表2,轨道板的横向应力受路基沉降的影响较小,最大横向拉应力发生在3号板的底面轨下位置,最大横向压应力发生在1号板的顶面轨下位置,路基沉降量从0增加到30 mm,分别增加了20%和40%；轨道板的纵向应力受路基沉降的影响较大,最大纵向拉应力发生在1号板的顶面中间位置,最大压应力发生在3号板的顶面轨下位置,随着路基沉降量从0到30 mm的增长,分别增加2.2倍和3.5倍。应力峰值出现在荷载正下方。

(2)沉降对垂向应力、垂向位移的影响

列车荷载经过3号轨道板时,在0沉降时垂向动应力峰值为0.468 MPa,在沉降为30 mm时为0.694 MPa,增大了48%,动位移在路基0沉降时峰值为0.6 mm,在沉降幅值为30 mm时,最大的垂向动位移为2 mm,随着路基不均匀沉降深度的增大,动位移增幅较大。 应力均随着路基沉降幅值的增大而增大,20 mm沉降之前增长较快,20 mm之后增长渐缓。

(3)轨道板易破坏部位分析

图4为随着路基沉降量的增大,3块轨道板最大拉应力的增长趋势图。路基沉降幅值的增加对2号轨道板的最大拉应力几乎没有影响,对1号和3号轨道板影响较大,1号板最大拉应力随沉降量的增加在30 mm范围内几乎呈线性增长,而3号轨道板最大拉应力在20～30 mm增长渐缓。

图3 不同沉降下轨道板底面横、纵向应力随位置的变化曲线

图4 路基沉降量对轨道板最大拉应力的影响

1号轨道板的顶面中间和3号轨道板的底面中间易出现较大的拉应力,且受沉降的影响较大,由于混凝土的抗拉强度较低且轨道板不允许出现裂缝,此两个部位成为轨道板易破坏部位,1号轨道板的上表面中间在沉降达到30 mm时,最大拉应力为1.41 MPa,如果按照C50混凝土抗拉强度设计值1.9 MPa,再乘以一个0.7～0.8的疲劳强度修正系数,已经达到限定值。

2.2 路基不均匀沉降对混凝土底座的影响

混凝土底座与路基表层直接接触,路基的不均匀沉降直接影响底座的受力。通过轨道-路基耦合模型的计算分析,将移动荷载作用下的混凝土底座各向应力、动位移幅值列于表3中,以对比不同的路基沉降量对混凝土底座的力学影响。

(1)不同路基沉降量对动应力的影响

图5为3号混凝土底座底面轨下中间位置节点的纵向应力随时间的变化曲线，随着路基沉降量的增大，纵向拉应力增加了3.3倍。

图6为荷载行至3号混凝土底座上方时,在不同的路基沉降量下,底座底面轨下位置的纵向应力随位置坐标(沿板长方向)的变化,最大的应力出现在底座的中间位置而非荷载正下方，有别于轨道板,随着路基沉降量的增大底座所有位置的纵向应力均较大增长。

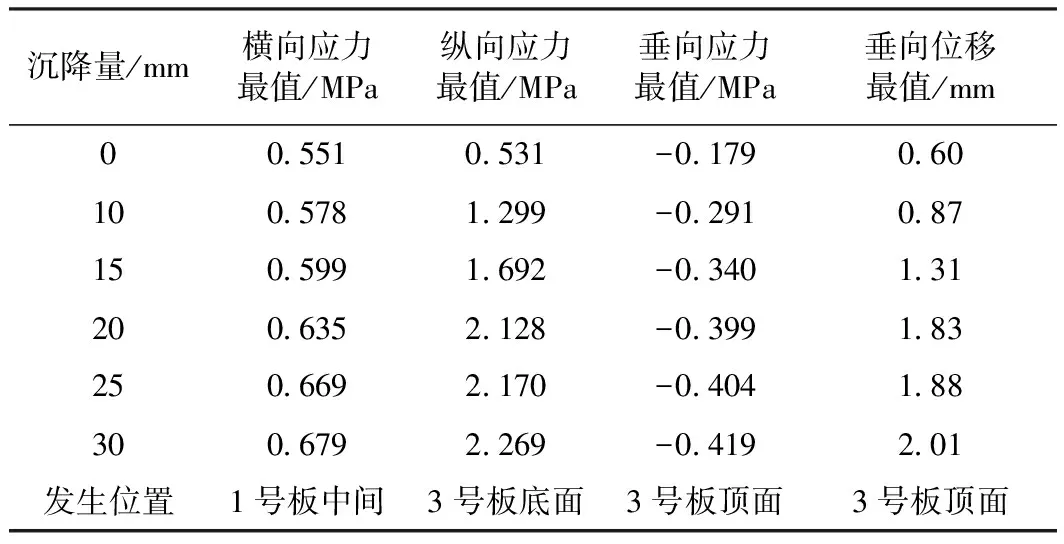
表3 不同沉降量下混凝土底座的力学响应

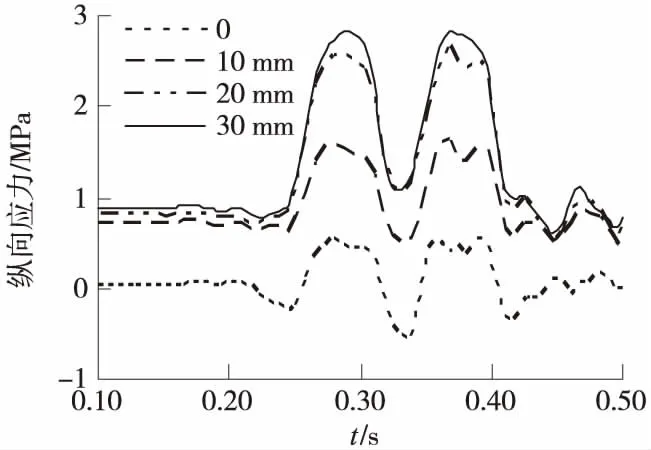
图5 不同沉降下底座底面节点纵向应力随时间变化曲线

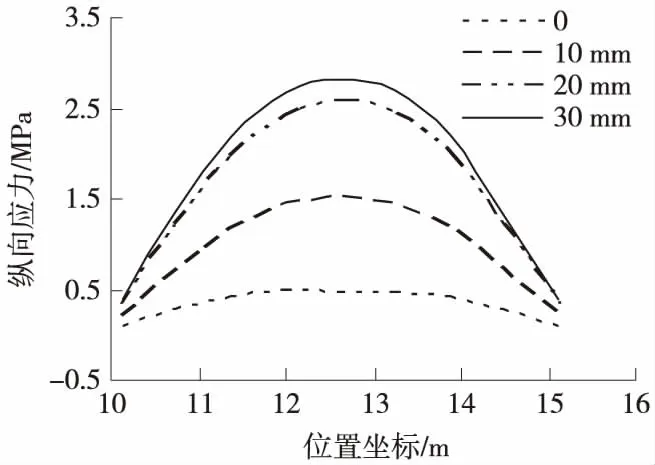
图6 不同沉降下底座底面纵向应力随位置的变化曲线

结合表3,混凝土底座的横向应力受沉降的影响很小,增长了23%,对垂向应力有较大的影响,在0沉降时垂向动应力为0.18 MPa,在沉降为30 mm时垂向动应力为0.42 MPa,增大了1.3倍,呈先陡后缓的增长趋势。图7为3号混凝土底座的动位移随沉降的变化曲线,在沉降达到30 mm时最大动位移达到2 mm。

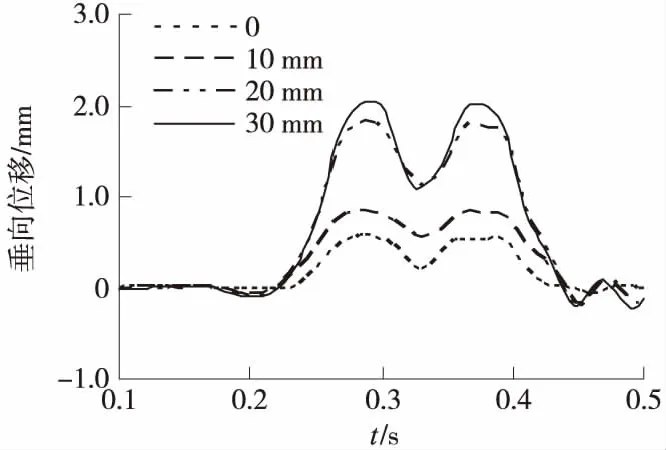
图7 不同沉降下混凝土底座动位移随时间的变化曲线

(2)混凝土底座易破坏部位分析

图8为3块混凝土底座板随路基沉降量的增大其最大纵向应力的发展趋势。可以看出路基的沉降量对1号和3号混凝土底座影响较大,1号混凝土底座的底面易随着路基沉降量的增大产生较大的压应力,但远小于混凝土的抗压承载力,拉应力也未造成破坏影响,而3号混凝土底座的底面随着路基沉降量的增大产生较大的拉应力,尤其在0～20 mm的沉降范围拉应力增长迅速，之后增长趋势渐缓,在20 mm的沉降时,已经超过了C40混凝土的抗拉承载力,由于路基的不均匀沉降较难控制,且易发生局部的沉降,致使底座与路基局部脱空,因此混凝土底座底面受拉钢筋的配置较为重要。

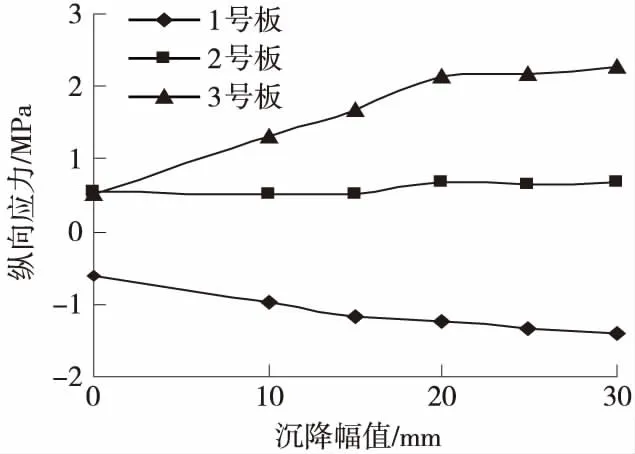
图8 路基沉降量对混凝土底座最大应力的影响

通过表3可知,同轨道板的规律一致混凝土底座的横向应力受路基沉降的影响不大,但是纵向应力受沉降量的影响较大,尤其是3号混凝土底座的底面从0沉降到沉降量30 mm，纵向应力增大了3.3倍,3号底座板处于沉降凹槽的最底部,当沉降过大易形成简支形式,是易发生破坏的部位；混凝土底座顶面的垂向动应力和动位移随路基不均匀沉降幅值的增大而增大,可以看出当路基的正余弦型不均匀沉降量增大时,3号混凝土底座最易发生破坏。

3 结论

(1)正余弦型路基不均匀沉降值对轨道板和混凝土底座的纵向应力、垂向应力、动位移影响较大,路基沉降量从0 mm增加到30 mm,呈先陡后缓的增长趋势,拐点为20 mm沉降量。

(2)正余弦型路基不均匀沉降对处于沉降槽起始位置的1号和处于沉降槽中间的3号轨道板、混凝土底座的影响较大,对处于沉降槽“腰部”的2号板影响较小,混凝土构件的纵向应力随路基不均匀沉降幅值的增大而增大,横向应力受沉降影响较小；尤其是1号轨道板的顶面中间和3号混凝土底座的底面是易发生破坏的部位。

(3)在路基余弦沉降幅值为20 mm/20 m时,3号混凝土底座的最大拉应力达到2 MPa,已经达到素混凝土破坏的极限强度,混凝土底座的最大拉应力大于轨道板的最大拉应力,因此混凝土底座底层受拉筋的配置较重要,混凝土底座的破坏会直接导致CA砂浆和轨道板的破坏,影响行车安全。

(4)通过建立轨道-路基三维有限元模型,在移动荷载作用下,分析的不同路基不均匀沉降幅值对板式轨道混凝土构件动力特性的差异影响,以及对混凝土构件的强度分析,可板式轨道的设计和维修提供参考。

[1] 王炳龙.高速铁路路基工程[M].北京：中国铁道出版社,2007．

[2] 蔡成标,翟婉明,王开云.遂渝线路基上板式轨道动力性能计算及评估分析[J].中国铁道科学,2006,27(4)．

[3] 刘成轩,翟婉明.轨道板强度问题的有限元分析初探[J].铁道工程学报,2001,3(1)．

[4] 刘茹冰.路基不均匀沉降对板式轨道动力学影响分析[D].成都：西南交通大学,2008.

[5] 赵国堂.高速铁路无砟轨道结构[M]. 北京: 中国铁道出版社,2006．

[6] 韩义涛,姚 力.基础沉降对土路基上板式轨道动力性能影响分析[J].铁道工程学报,2007(10)．

[7] 王其昌,韩启孟.板式轨道设计与施工[M]. 成都: 西南交通大学出版社,2002．

[8] 娄 平,曾庆元.移动荷载作用下板式轨道的有限元分析[J].交通运输工程学报,2008,25 (12)．

[9] 卿启湘.高速铁路无砟轨道-软岩路基系统动力特性研究[D].长沙：中南大学,2005．