场量子及其薛定谔波的物质属性＊

赵国求

（华中科技大学－WISCO联合实验室，湖北武汉430080）

场量子及其薛定谔波的物质属性＊

赵国求

（华中科技大学－WISCO联合实验室，湖北武汉430080）

由R＝2π／λ＝1／r＝P／ħ定义场量子的量子曲率，则量子曲率为场量子建构了一个可认知的“空间形态”。在量子伴生空间r是场量子的空间占位，在外部物理空间r＝△x则是“点量子”的位置测不准量。同点粒子抽象一样，量子曲率R是对与场量子相伴生的波动物质形态的抽象，而且点粒子抽象只是量子曲率R＝∞的特例。

场量子；量子曲率；量子伴生空间

为了揭示波函数如何描述微观量子客体的时空特征，我们从爱因斯坦及德布罗意的两个基本公式

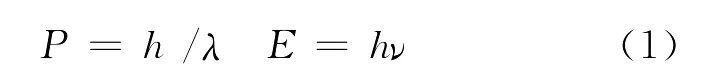
出发。

方程的左边P和E是场量子作为质点所承载的动量和能量，它们均是外部物理空间中的可观察量。方程的右边是与场量子对应的德布罗意─薛定谔波ψ的频率和波长，也应是可观察量。但ψ波不描述在外部物理空间，而是描述在量子伴生空间［1］，波不可直接观察。但波与粒子相伴生，我们赋予粒子以物质实在性，与之相伴生的ψ波也应有物质实在性。方程（1）中，等号表明外部物理空间中物质的“点描述”与量子伴生空间中物质“波动描述”的等价变换。现在要问，量子伴生空间中的这个波，到底是物质的什么波？场量子在什么条件下展示出波动性？

对于微观量子客体——场量子而言，能量的测不准量是△E＝E，动量的测不准量是△P＝P，对方程（1）作如下变形：

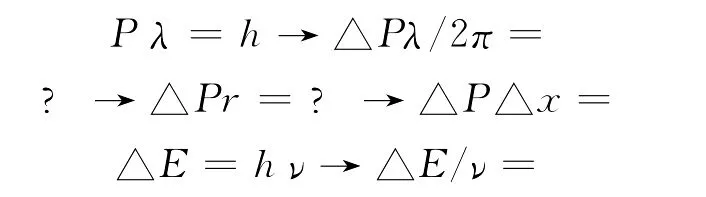
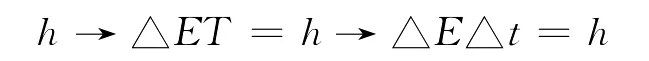
讨论：

1．因为r＝λ／2π，λ为圆周，则r为此圆的半径。波长有空间概念，r为场量子建构了一个可认知的“空间形态”。r＝△x≠0，表明场量子在量子伴生空间有“空间占位”，位置有测不准量，体现微观量子客体不是“点”，而是在动量作用下出现一个空间的广延性。这就是测不准关系△P△x＝ħ的真实物理意义。在量子伴生空间r是场量子的空间占位，在外部物理空间△x则是“点量子”的位置测不准量。r＝△x在量子伴生空间和外部物理空间有了等价表述。若定义R＝1／r为场量子的量子曲率，则量子曲率：

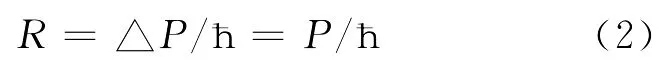
场量子的动量决定了场量子的量子曲率。它是一个空间弯曲的量度，呈现“非点场量子”物质的空间特性，也是物质存在形态，并描述在量子伴生空间。同点粒子抽象一样，量子曲率R则是对与场量子相伴生的波动物质形态的抽象，而且点粒子抽象只是量子曲率R＝∞的特例。

2．1／ν＝T，ν是量子伴生空间薛定谔波的频率，T是此波的周期。如果我们取△E＝E，E是场量子的能量，那么，T＝△t，也就是产生“场量子”能量E的积累周期，是过程量。体现为场量子自身能量和时间的测不准关系：△E△t＝h。一个场量子自身的形成是连续过程，构成连续物质场，但场量子之间是突变断裂的。这正好对应本征态ψn自身的连续性和态与态之间的突变性。当态与态之间动量的突变性消失时，态之间的突变性消失。

3．现在我们得到一个以量子曲率R为模，描述场量子自身“非点粒子”物质特征，周期变化着的，复平面上的“旋转物质振子”。当场量子在时空中运动时，就表现出对应量子曲率的波动，我们称之为曲率波。曲率波是物质波。它就是大家熟悉的薛定谔波。

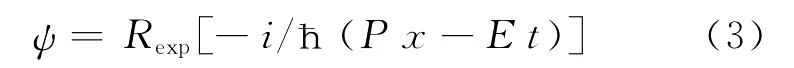
ψ所在的空间就是量子伴生空间。它总是与场量子联系在一起的，符合量子力学曲率解释公设体系［2］。式（3）与玻姆物质波的形式一致，但赋予了ψ明确的物理意义——曲率波。曲率的大小表示粒子性，曲率的变化表示波动性。当曲率等于无穷大时，微观量子客体就抽象成质点，两种模型具有内在同一性。波、粒和谐统一，两种模型都具有物质实在论意义。

微观量子客体质“点”，由“量子曲率”显示其物质特征，并通过“曲率振子”的运动展现其波动形态。量子力学中，现有薛定谔波所有的具体数学形式中，其振幅中均可分离出一个曲率因子，表示成曲率波形式。曲率波概念是普遍适用的［3］。

其实，我们与德布罗意思想有类似性，德布罗意也认为与实物粒子对应的有一个内在的振动，并随粒子的运动形成波［4］。但德布罗意对振动物理意义的理解没有做出充分说明，因而波的物质性不好理解，而曲率波的物质性却很好理解。

物质波ψ与场量子相伴生，但“点描述”与“波描述”分别在两种不同的空间。在量子力学曲率解释中，式（1）的物理意义代表外部物理空间中点粒子描述到量子伴生空间物质波波动描述的等价转换。转换的条件就是薛定谔波的波长与缝宽可以比拟，对光量子如此，对电子也是如此。曲率波理论中，上述条件转化为：场量子“曲率波波长（或曲率半径）”与缝宽差不多时将表现出力学运动的波动性。此时质点模型不适用，描述场量子必须用量子曲率模型，也就是曲率波模型。德布罗意所谓“点粒子内部”，其实就是一倍波长建构的“圆周”内。场量子的波动性是在接近物质波波长的环境条件下出现的。

场量子物质表现形态的转换与所处外界环境相关，可做出经典类比。设计师做船体设计，船体受力必须考虑水波波长与船长的关系。当波长比船长远远大于和远远小于之时，轮船可当作质点，轮船的运动就是质点的运动。但当波长和船长差不多时，船体的受力就不能当质点处理了。此时船体的受力必须用新的力学模型，必须分析船体受力在船体内部的传播。如果我们有“内视功能”，也将会在外部物理时空每个不同时空点上，“看到”船体内“物质”的波动运动，也存在一个外部物理时空“质点描述”到伴生空间“波动描述”的转换。对于外部物理时空而言，波函数的整体性是不言而喻的。

光量子（场量子）之于双缝，可类比船之于海浪波长。

我们再看量子伴生空间中的曲率波与外部物理空间中的概率波之间的关系。

我们是用外部物理空间中点粒子概率波的波长λ为场量子在量子伴生空间中建构形体结构的，概率作为一种属性已自然进入场量子的构形之中。曲率R，与波长λ成反比，与动量P成正比。这与实际情况刚好一致。在原子内部，靠近原子核，波长短，动量大，曲率R大，电子出现的概率高；在原子的外层，波长长，动量小，曲率R小，电子出现的概率低；在零势面上，波长无限大，动量为0，曲率为0，电子出现的概率为0。量子伴生空间中场量子的“量子曲率”R与外部物理空间中场量子点描述出现的概率ρ成正比：ρ∝R。R＝∞，场量子收缩成点，概率ρ＝1。曲率R与概率ρ及曲率波与概率波有了内在联系。曲率波包含有外部物理空间中概率波属性［5］。外部物理空间与量子伴生空间，两种空间描述方式的转换是逻辑自洽的。

光量子的薛定谔波是否等价于爱因斯坦的光量子电磁场，可以通过两种空间的转换进行讨论。在外部物理空间中光量子是质点，是粒子流；粒子是实的，波是虚的、场是“鬼”，是统计波或概率波。在量子伴生空间中光量子有构形，光量子用曲率波描述，波是实的、物质的，粒子是虚的，粒子是“鬼”。我们认为，正是这种转换揭示了量子测量的物理实质。量子测量时，光量子从非连续作用过渡到连续作用，作用量子从h≠0过渡到h＝0。光量子的描述方式将从量子伴生空间的实体波、虚粒子转换到外部物理空间的实粒子、虚波。光量子是波粒二象性的统一，看你在什么层次的环境中用什么模型去描述它，观察它。

光量子的薛定谔波是在量子伴生空间对光量子的波动描述；爱因斯坦的光量子电磁波或狄拉克量子场论是在外部物理空间对光量子的点粒子描述。两者可以转换，但不是简单相等，但对薛定谔波和电磁场的物质性要求是基础。薛定谔波场和连续物质场（电磁场）有内在联系，这就为连续物质场的能量量子化与薛定谔波场的量子化架起了沟通的桥梁。

狄拉克否定“有与电子联系的真实物质波的存在”，把薛定谔波等同于概率波［6］211。而狄拉克粒子数表象变换理论的罗辑起点是薛定谔波，因而不是真实物质场的量子化。这是狄拉克量子场论中概念混淆的总根源。狄拉克粒子数波函数表象变换，将概率波变成粒子数波，这里“场”前后都不是真实的。但表象变换隐含将多粒子概率波中“可能粒子数”转换成爱因斯坦粒子“系综”中的“真实粒子数”，并确立基本本体是爱因斯坦光量子的概念转换。这个概念转换的物理基础是什么？狄拉克没有做出令人（包括他自己）信服的回答。性质不同的多级概念转换，是通过人为数学操作实现的！将多粒子出现的概率变成了真实多粒子分布，将“可能”变成了“真实”！“可能”如何在表象变换中就变成“真实”了呢？总让人觉得逻辑上很靠不住，而且实验中单光子通过双缝自相干问题狄拉克也没有解决。

一个数学波（概率波）通过表象变换就将“可能粒子数”变成“真实粒子数”让人难以思议，这里仍深刻涉及波函数的实在性问题。所以我们说ψ场概率解释遇到的困难是根本性的。我们必须对德布罗意─薛定谔波场做出实在论解释：承认“有与电子联系的真实物质波——曲率波的存在”。量子力学曲率解释中薛定谔波的物质性及对量子测量物理过程的理解，无疑消解了狄拉克的这一逻辑矛盾。这与爱因斯坦放弃以太，承认电磁场自身的物质性有异曲同工之妙。

量子力学曲率解释中建立量子场论的基本思路是：

第一，在量子伴生空间场量子可抽象成曲率R，它与场量子在外部物理空间抽象成质点具有同等数学物理意义。点粒子抽象是量子曲率R＝∞时的特例。曲率波既描述单粒子，也描述多粒子，但具有物质性，描述在量子伴生空间，是场量子在“h≠0”的环境中表现的物质新形态。

第二，量子测量能将非连续作用转化为连续作用，并从“h≠0”的环境转化为“h＝0”的环境；描述方式也将从量子伴生空间的实体波、虚粒子的波描述转换到外部物理空间的实粒子、虚波的点粒子描述，从而获得爱因斯坦的光量子粒子“系综”。

第三，经典电磁场理论中，普通光波是外部物理空间中连续物质场的能流密度分布（经典场论），基本本体是连续场，亦或是外部物理空间中多光子爱因斯坦统计“系综”，基本本体是粒子；多光子德布罗意—薛定谔波则是量子伴生空间中的曲率波。基本本体是曲率波。普通光波与光量子的德布罗意—薛定谔波（曲率波）是两种不同概念［6］205－223，但两者在物质波的基础上通过量子测量可以等价转换。

第四，狄拉克粒子数表象变换、矩阵对角化、算符从非对易到对易的转化、场的激发与退激，是上述量子测量物理原理在量子场论中的数学程式表达，粒子数波函数描述的是外部物理空间爱因斯坦的“点”粒子“系综”。外部物理空间点粒子模型与相互作用的连续性，奠定了薛定谔波场光量子、爱因斯坦光量子、连续物质场的能量子三者之间经典区别的模糊性。

第五，量子力学曲率解释中，由于曲率波的物质性，多粒子薛定谔方案物质波每个定态的光量子数Nr’、物质场（电磁场）场分量中能量子数Nr，与爱因斯坦粒子“系综”场分量粒子数N；薛定谔波场（物质波）的光量子、爱因斯坦的光量子与物质场（电磁场）的能量子就有了必须的物质基础。于是狄拉克“把光量子的性质给予辐射”就能办到。而这种“能办到”，刚好涉及到量子测量中，两种不同空间点粒子描述与波动描述的等价转换。转换的逻辑程序是：曲率波（物质场）纯态（ψ＝∑anψn，定态、定态跃迁，能级间动量Pn不连续，作用不连续，h≠0，量子伴生空间ψ场描述）→量子测量（A）→混合态（本征态、本征值连续，Pn连续，作用连续，连续物质场，h≠0，量子伴生空间ψ场描述）→量子测量（B）→经典态（作用连续，h＝0，外部物理空间质点描述）。

狄拉克场量子化的真正起点是经典辐射场，场能的量子化与薛定谔波量子化及粒子数表象变换的逻辑矛盾通过上述逻辑程序消解了［6］211。

我们认为，上述基本思路可以清除曹天予先生所说，狄拉克量子场论中所存在的一些基本概念混淆，更为约当将狄拉克量子场论推进到费米子，做了坚实的逻辑与理论基础辅垫。问物质怎么会是曲率波与问物质怎么会是点粒子意义等同。这里，关键是承认波函数的物质性，承认曲率波是一种物质存在的新形态，并描述在量子伴生空间。这就是我们建立量子力学曲率解释的又一个理由。

注释：

① “量子伴生空间”：1）采用希尔伯特空间数学方法；2）空间的平直性与粒子运动状态相关，即与波函数时空坐标的变换性质相关。

［1］ 赵国求，鲍得海．相对论时空、“量子伴生空间”、物质波及规范变换［M］．中国：武汉大学，2009年7月，第一届国际结构实在论与量子力学哲学问题学术研讨会，217－229．

［2］ 赵国求，鲍得海．量子力学曲率解释中的基本假设［M］．中国．武汉大学，2009年7月，第一届国际结构实在论与量子力学哲学问题学术研讨会，193－202．

［3］ 赵国求．从相互作用实在到量子力学曲率解释［M］．武汉：武汉出版社，2008：455．

［4］ 倪光炯，李洪芳．近代物理［M］．上海：上海科学技术出版社，1979：146－148．

［5］ 赵国求，桂起权，等．物理学的新神曲［M］．武汉：武汉出版社，2004：250－251，285－286．

［6］ 曹天予．20世纪场论的概念发展［M］．吴新忠，译．上海：上海教育出版社，2008．

Field Quantum and Physical Properties of Its Schrodinger Wave

ZHAO Guo－qiu
（WISCO Associated Lab，Huazhong University of Science and Technology，Wuhan 430074，Hubei，China）

A cognizable“spatial pattern”about field quantum is constructed by Quantum curvature whose field quantum is defined by R＝2π／λ＝1／r＝P／h，where is the spatial placeable of field quantum in quantum associated space，and r＝Δχis the uncertainty quantity of position of“point quantum”in outside physical space．Like the abstraction of point particle，quantum curvature R is the abstraction of associated wave physical pattern of field quantum，and point particle abstraction is only a special or even exceptional case when quantum curvature R＝∞．

field quantum；quantum curvature；quantum associated space

B028；N02

A

10．3963／j．issn．1671－6477．2010．06．017

2010－06－30

赵国求（1944－），男，湖北省黄梅县人，华中科技大学－WISCO联合实验室研究员，北京师范大学、华南理工大学科学技术哲学中心兼职教授，湖北省自然辩证法研究会常务理事、物理学哲学专业委员会主任，武汉工程职业技术学院研究员。

2007年国家教育部青年基金资助课题（07JC720016）；武汉钢铁（集团）公司项目（编号（2009）技合字22号）

（责任编辑 易 民）