非饱和带水分特征曲线经验公式研究

李云龙，郭春颖，徐 敏

(1.中国矿业大学(北京)，北京 100083； 2.中国地质工程集团公司， 北京 100083)

非饱和带(也称包气带)中发生着各种物理的、化学的、生物的变化，存在着气相、液相等流体的流动以及各种物质成分之间的迁移和转化，加之人类活动的叠加和各种污染物质的排放，致使非饱和带水分的迁移和转化过程十分的复杂。

非饱和带水的运动是非饱和带营养物或污染物运移以及热运动的主要驱动力；水资源评价和预报需要掌握水分在非饱和带中的运动和分布规律；土壤物理、水利工程和水文计算等许多应用和研究领域都需要研究非饱和土壤水分运动规律；对土壤水分运动规律进行研究也是发展精准农业、生态农业的必要前提。另外，土壤侵蚀、地下水污染、地下水资源评价、土壤退化、荒漠化问题、灌溉制度、土壤污染、土壤改良、径流分析、水利工程、地基基础变形等一系列理论和实际问题都与非饱和带密切相关。

土壤水分特征曲线表示土壤水的能量和数量之间的关系，是研究土壤水分的保持和运动所用到的反应土壤水基本特征的曲线。土壤水分特征曲线在研究土壤水分流动和溶质运移中有着非常重要的作用。由于它们之间的关系复杂，难以从理论上推导出确切的关系式；但通过大量的试验研究，人们已提出了许多经验公式来描述它，本文以获得准确的水分特征曲线参数为目标，在参考和借鉴前人成果的基础上，精心设计和改进实验仪器，提出合理的实验方案，历时约一年时间。获得了5种砂土实测数据。以土壤水动力学为指导，借助Matlab软件，在比较算法的基础上，采用具有代表性的六种经验公式模型对实测数据进行了拟合。

1 非饱和带水分特征曲线的测定

1.1 实验材料

实验介质共有5种，取自渭河中上游。分别命名为：筛选1#样、筛选2#样、扰动1#样(渭南砂样)、扰动2#样(渭南砂样)、渭河西安段砂样。

其中：筛选1#是粒径为0.5～1mm，干容重为1.514g/cm3；筛选2#是粒径为0.25～0.5mm，干容重为1.501g/cm3；扰动1#、扰动2#没进行筛选。各试样颗粒组成详见表1。

1.2 实验数据

土壤水分特征曲线实测数据见表2。

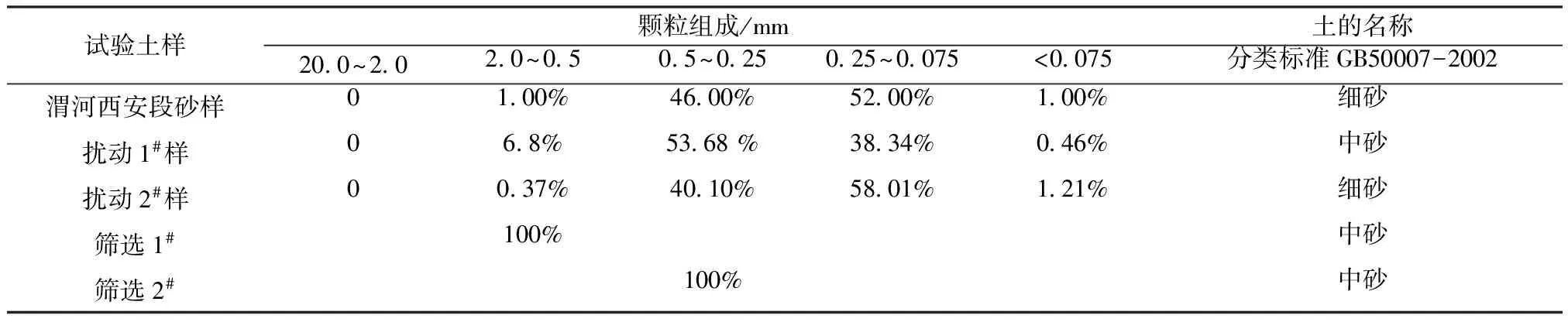
表1 试样的颗粒组成

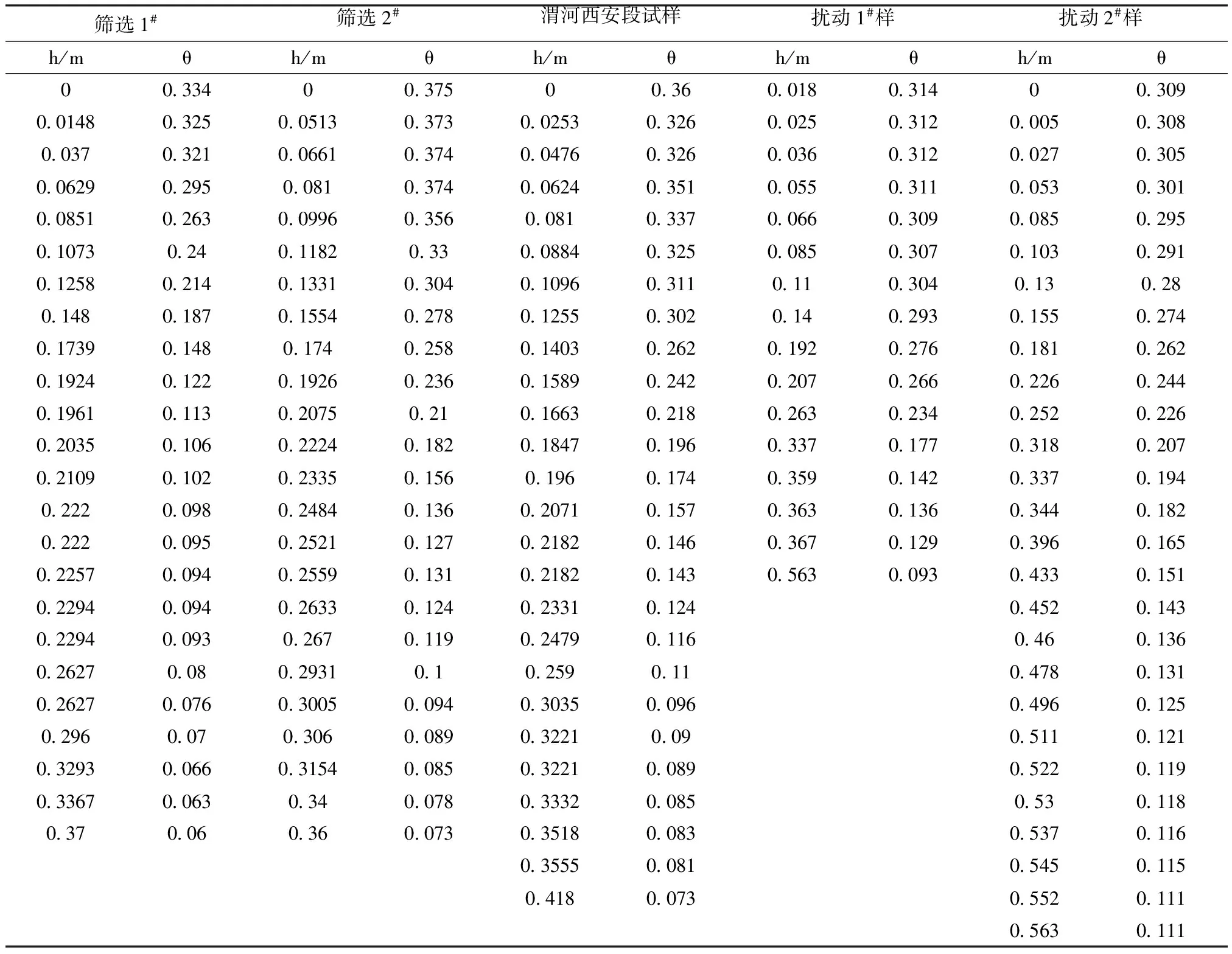
表2 土壤特征曲线试样数据

2 非饱和水分特征参数的拟合

2.1 常用经验公式

比较常用经验公式的有：Brooks-Corey(1964)模型，Gardner(1970)模型，Van Genuehten(1980)模型、Gardner-Russo(1988)模型、Mckee和Bumb(1984)、Frdlund和Xing(1994)、Broadbridge—White、Campbell模型、Williams(1983)、Burdine模型等。这些模型中都含有许多待求的参数。各模型见(1)～(8)。

本文借助于Matlab软件，对拟合效果较好，具有代表性的Brooks-Corey(1964)模型、VanGenuehten(1950)模型、Gardner-Russo(1988)模型、Mckee和Bumb(1984)、Frdlund和Xing(1994)、Broadbridge—White模型中的参数进行拟合，比较拟合效果。

(1)Brooks-Corey模型(简称B-C模型)

(1)

式中：Se是饱和度；θ是体积水分含水量 (L3L-3)；θs和θr分别为饱和含水量和残余含水量(L3L-3)；hb为进气压力(或起泡压力)值(L)；h是压力水头(L)；γ是大于零的正常数，它反映了土壤的空隙大小分布。

(2)Van Genuchten模型(简称VGM模型)

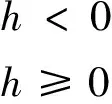
(2)

式中：θ是体积含水量(L3L-3)，θs和θr分别为饱和含水量和残余含水量(L3L-3)；h为压力水头(L)；α(L-1)是与进气值有关的参数，n是曲线形状参数，m=1-1/n(m=1-1/2n或m=n)。

(3)Gardner-Russo模型

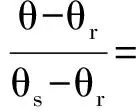
(3)

式中：Se是饱和度；θ是体积水分含水量 (L3L-3)，θs和θr分别为饱和含水量和残余含水量(L3L-3)；h为压力水头(L)；α(L-1)和m是水分特征曲线的形状参数。

该模型是Russo(1988)借助于Gardner(1958)模型(表示非饱和水力传导率与压力水头之间的关系)，即

(4)

式中：α是一个土壤参数(L)，代表水力传导率随着压力水头的减小而减小的相对速率；Ks是饱和水力传导率(LT-1)；h是压力水头(L)。

(4)Mckee和Bumb(1987)

(5)

θs和θr分别为饱和体积含水量和残余体积含水量(L3L-3)；Ψ为吸力值(L)；a、b为拟合参数。

(5)Frdlund和Xing(1994)

(6)

式中：θs饱和体积含水量 (L3/L3)；a为与进气值有关的参数；b为在基质吸力大于进气值之后与土体脱水速率有关的土参数；C为与残余含水量有关的参数

(6)Broadbridge—White模型

Broadbridge和White(1988)建立的土壤基质势与土壤相对含水量的函数关系表达式：

式中：θ为容积含水量，θr为土壤残留含水量，θs为饱和含水量；ψ为土壤基质势；λ为反映孔隙大小分布的参数；C为土壤结构参数；Θ为无量纲含水量，即相对含水量，用如下公式计算：

基于当土壤含水量为θr时的导水率Kr近似为零的假定，Broadbridge和White推导的土壤导水率K计算公式为：

(8)

式中：Ks为饱和导水率；其他同上。

2.2 参数拟合方法

土水特征曲线实测数据较多，如果采用线性回归或非线性拟合的方法进行计算，计算极为复杂，且易出现无解的情况。本文采用一种非线性回归与最优化相结合的方法估计或非线性最小二乘拟合各参数的值。而且要计算模型中的参数只有通过计算机编程实现才较容易。本文采用MatLab软件变成对参数进行拟合。

2.3 拟合结果比较

用Matlab分别对筛选1#、筛选2#、渭河西安段砂样、扰动1#、扰动2#用不同土水特征曲线模型进行拟合，可得到无约束的条件下拟合曲线，其中筛选1#、筛选2#拟合曲线见图1、图2，各模型拟合参数值见表3、表4。

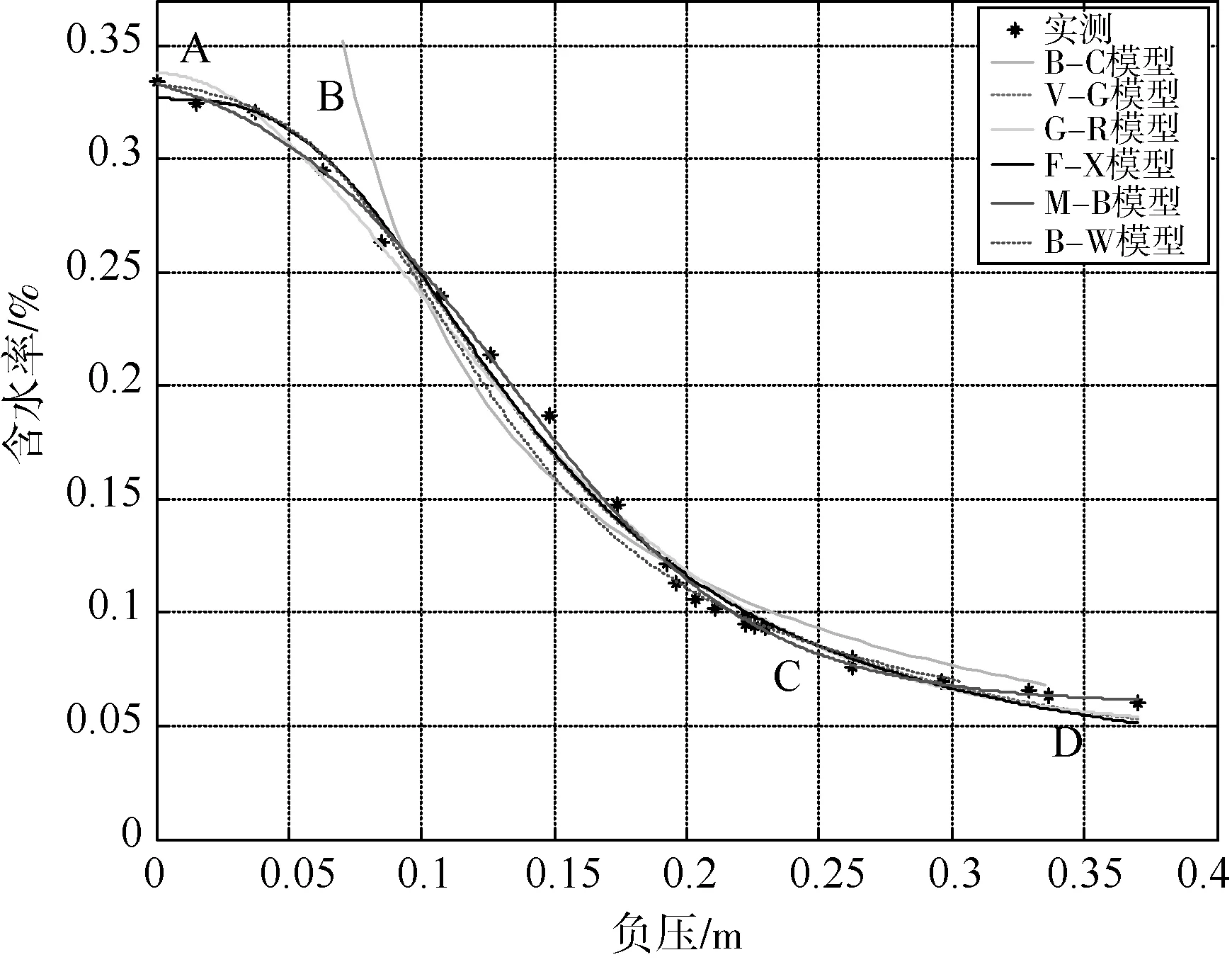
图1 六个模型对筛选1#砂样拟合结果图

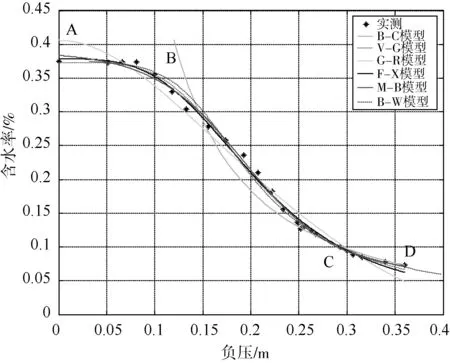
图2 六个模型对筛选2#砂样拟合结果图

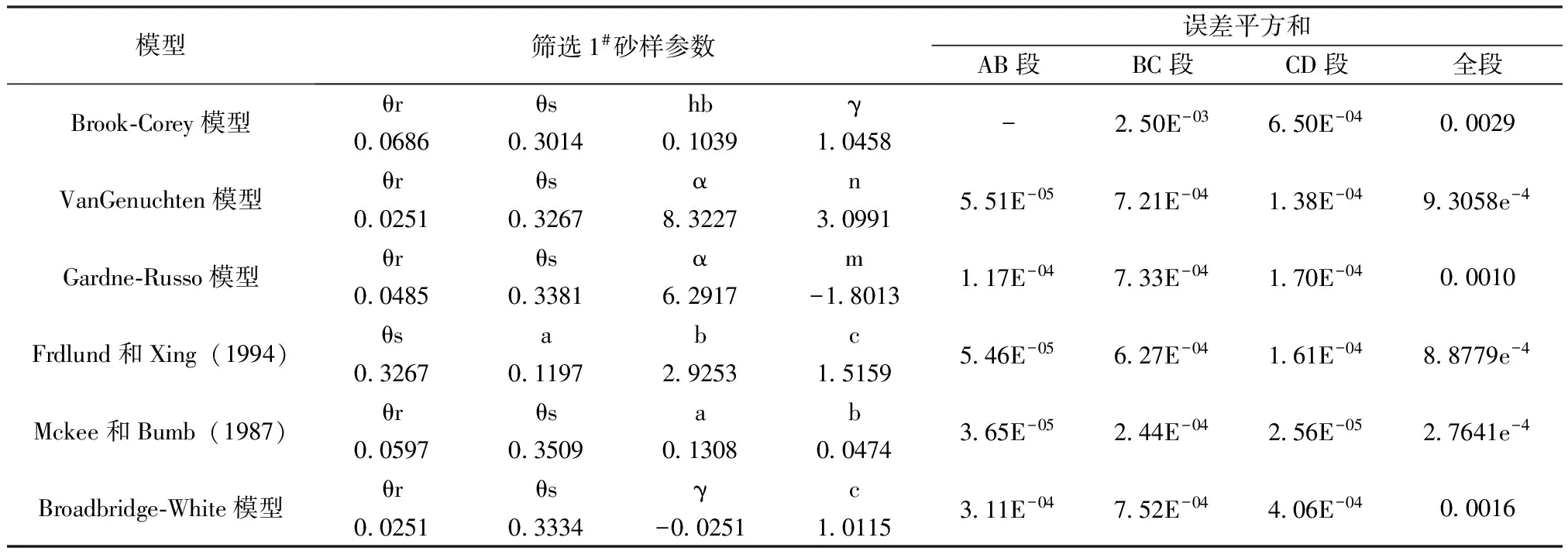
表3 不同模型对筛选1#砂样拟合参数结果

表4 不同模型对筛选2#砂样拟合参数结果

从图1筛选1#拟合曲线和表3不同模型对筛选1#砂样拟合参数结果上看，Mckee和Bumb(1987)模型、Van Genuchen模型、Frdlund和Xing(1994)模型拟合效果较好。在A—B段Mckee和Bumb(1987)模型拟合效果最好，Gardner-Russo模型、Frdlund和Xing(1994)模型次之，同样在B—C和C-D段，Mckee和Bumb(1987)模型拟合效果最好，而其他模型误差平方和较大。Mckee和Bumb(1987)模型在整个拟合曲线偏离度最小。误差平方和为2.7641e-4。

从图2筛选2#拟合曲线和表4不同模型对筛选1#砂样拟合参数结果可以看出，Mckee和Bumb(1987)模型、Van-genuchen模型、Frdlund和Xing(1994)模型拟合效果较好。在A—B段Van-genuchen模型拟合误差平方和最小，Mckee和Bumb(1987)模型和Frdlund和Xing(1994)模型次之；在B—C段Mckee和Bumb(1987)模型误差平方和最小，Frdlund和Xing(1994)模型次之；在C—D段Mckee和Bumb(1987)模型误差平方和最小，其它模型误差平方和较大；在整个负压范围内Mckee和Bumb(1987)模型误差平方和最小。误差平方和为9.0904e-4。

渭河西安段试样拟合曲线结果为，Mckee和Bumb(1987)模型、Van-genuchen模型、Frdlund和Xing(1994)模型拟合效果较好。在A—B段Mckee和Bumb(1987)模型拟合误差平方和最小；在B—C段Mckee和Bumb(1987)模型误差平方和最小，Van-genuchen模型次之；在C—D段Van-genuchen模型误差平方和最小，其他模型误差平方和较大；渭河西安段砂样为细沙，Frdlund和Xing(1994)模型中θs取值范围为0.33～0.35，a值在 0.10～15间，b值在 4 ～5间，c值在0.5～1间。计算值与实测值拟合较好，且与实际偏离度为7.7444e-4； Van-Genuchten模型中θr取值范围 为0.06～0.08，θs取值范围 为0.33～0.35，a值在5～8间，n值在 4～5间。计算值与实测值拟合较好，且与实际偏离度为6.1521e-004；Mckee和Bumb(1987)模型中θr取值范围 为0.073～0.081，θs取值范围为0.33～0.35，a值在 0.15～0.2间，b值在 0.04 ～0.05间。计算值与实测值拟合较好。误差平方和为4.5172e-4；在整个负压范围内Mckee和Bumb(1987)模型误差平方和最小。同样Mckee和Bumb(1987)模型对扰动1#、扰动2#实测数据拟合偏离度也是最小。

3 结论与建议

3.1 结论

对Brooks-Corey模型、Van-genuchen模型、Frdlund和Xing(1994)模型、Mckee和Bumb(1987)模型、Gardner-Russo、Broadbridge—White模型拟合效果进行比较，总体而言，4参数方程的拟合效果要优于3参数方程。在4参数方程中，Mckee和Bumb(1987)模型的拟合效果最佳且计算值符合实际情况。

参数拟合的结果表明Mckee和Bumb(1984)模型对于砂样拟合的偏离度最小，筛选1#的偏离度为2.7641e-4；筛选2#的偏离度为9.0904e-4；渭河西安段的偏离度为4.5172e-4，且拟合出的参数均符合实际。

3.2 建议

(1)建议对细颗粒土壤进行研究，可以在筛选样的基础上添加不同比重的粘粒进行实验。

(2)考虑温度对土壤特征曲线的影响，试样所用的仪器已经设计了电热器、温控仪和温度传感器等仪器，可以测量温度对土壤特征参数的影响。

[1] 雷志栋，杨诗秀，谢森传，等.土壤水动力学[M] . 北京：清华大学出版社，1988.

[2] 张蔚榛. 地下水与土壤水动力学[M]. 北京:中国水利水电出版社，1996，9.

[3] 杨金忠，等.多孔介质中水分及溶质运移的随机理论[M]. 北京：科学出版社.2000.9.

[4] 胡波,肖元清,王钊. 水-土特征曲线方程参数和拟合效果研究[J] . 三峡大学学报,2005，27(1).

[5] 韩锦萍.包气带水分运移的数值分析[D]. 长安大学环境科学与工程学院， 2005，6.

[6] 王红闪，黄明斌.四种方法推求土壤导水参数的差别与准确性研究[J].干旱地区农业研究，2004，22(2):76-79.

[7] 朱学愚,谢春红著. 地下水运移模型[M]. 北京：中国建筑工业出版社,1990,108-113.

[8] 陈洪松，邵明安，推求非饱和水分运动参数的间接方法[J]．应用基础与工程科学报，2002，10：103-109.

[9] 张蔚榛，张瑜芳．土壤水分运动参数的测定方法[J]. 水文地质工程地质，1981(2).

[10] 薛强，刘勇，刘建军，等.非饱和土水特征曲线模型参数反演辨别研究[J].仪器仪表学报，2006， 27(6):743.

[11] 来剑斌,王全九.土壤水分特征曲线模型比较分析[J]. 水土保持学报，2003，17(1)：137.

[12] 张俊，徐绍辉，刘建立，等. 土壤水力性质参数估计的影响界面和敏感度分析[J]. 水利学报，2005，36(4).

[13] 魏义长,等.土壤持水曲线Van Genuchten 模型求参的Matlab实现[J]. 土壤学报，2004，41(3).

[14] 钱天伟，陈繁荣，杜晓丽，等．一种推求van Genuchten方程参数的高性能优化方法[J]．土壤学报，2004，4l(6)：138-l40.

[15] Van Genuchten MTh．A closed-form equation for predicting the hydraulic conductivity of unsaturated soils．Soil Sci．Soc．Am．J．，1980，44(5)：892—898.