Matlab辅助工程静力学分析

曾德惠

(湖北民族学院 理学院,湖北 恩施 445000)

静力学在工程实际中有着极其广泛的应用,对零件结构的设计和改进,都应当首先进行受力分析.静力学是理论力学的重要组成部分,它研究物体的受力分析、力系的简化方法以及受力物体的平衡条件,其目的是求解未知力,为零件结构的进一步设计打下基础.静力学问题的求解,涉及大量符号运算和数值计算.采用传统计算方法需花费大量的时间,许多复杂问题的求题不得不过多地依赖技巧实现.用计算机取代计算器[1]早已是不争的现实.文献[2]中提出处理理论力学问题的新途径:把力学、计算数学和计算机软件结合起来,形成了理论力学问题→理论分析→选择合理的数值计算方法→程序编制→用计算机求得结果的解决模式.文献[3]中提出了在理论力学教学中应充分利用矢量、矩阵等数学工具,重视对学生计算机数值求解方法的训练,在具体的求解过程中选用Matlab或Maple软件工具. Matlab是一种面向科学与工程计算的高级语言,提供了强大的矩阵处理和绘图功能,给出了一个融合计算、可视化和程序设计的交互环境,操作简便,能高效求解各种复杂工程问题并实现计算结果的可视化[4,5].本文以静力学中的核心内容(力系简化和力系平衡)为研究对象,较为详细地讲述了Matlab辅助静力分析计算的过程,编制出的程序具有一定的普遍性,并给出了具体实例加以说明和验证.

1 Matlab求解静力学问题的方法步骤

1.1 建立力学模型

力学模型的建立是求解静力学问题的基础.模型的正确与否,直接关系到计算精度和计算工作量.针对具体问题,首先应确定研究对象;然后根据已知条件和约束类型,分清主动力和约束力,结合静力学基本概念和有关原理分析受力情况并画出受力图,建立坐标系.

对于特定的工程问题,涉及各式各样的物体,其实际状况有时是很复杂的.在建立力学模型时必须对这些物体进行必要的、合理的简化.由于静力分析与物体外形有关的只是载荷与约束的位置及类型,而与载荷和约束无关的外形是次要因素可以忽略.因而直接采用简单的线条来绘制研究对象,按照国家标准的规定画法表达力和约束的作用位置及类型,用计算简图来描述实际物体的全部受力情况.

1.2 建立数学模型

将力学模型转换为数学模型是编程计算的关键.工程实物抽象为力学模型后,要应用力学原理,充分利用矢量、矩阵、线性方程等数学工具,将力学模型用数学方法简洁地描述出来.例如:将力用矢量表示、力系简化用矢量运算求得、平衡方程组写成矩阵形式等等.

1.3 Matlab编程求解

Matlab编程方式有两种[6]:①行命令方式.即在命令窗口中输入一条或多条命令,然后执行,再输入-执行,完全以交互的方式进行.②M文件方式.即把程序写成一个由多行语句组成的文件,通过在命令窗口中输入文件名回车来执行这个文件.M文件分为脚本文件和函数文件两种,可以在其他的文本编辑器如记事本、写字板中编写,也可以在Matlab的程序编辑器中编写,并以“.m”为扩展名加以存储.Matlab软件用C语言编写,其语法与C语言十分相似,编写却更加简单方便.

2 Matlab用于力系的简化

力系的简化是静力学中一种重要的力学分析方法.只有运用力系简化才能将复杂的受力问题抽象成简洁的力学模型.比如运用力系的简化可以建立平衡方程,可以推导固定端约束处的约束反力、合力矩定理、物体重心位置等等[7].又如对刚体动力学问题,可以将刚体上每个质点的惯性力组成惯性力系,用力系简化的方法得出简化结果.然后根据达朗伯原理,用静力学建立平衡方程的方法求解动力学问题.

力系的简化,就是用一个最简单的力系等效地代替复杂力系,简化结果得到一个主矢和主矩.主矢是各力的矢量和,主矩是各力对简化中心的力矩求和[7].工程上常见的力系为两种：平面力系和空间力系.其中空间力系是最一般的力系,平面力系是空间力系的特例.许多工程结构和机械构件都受空间力系的作用,如车床主轴、桅式起重机、闸门等.Matlab求解时可以用向量或矩阵的形式将各个力表示出来,力系的简化即对这些向量或矩阵进行操作：如向量相加、向量点积和叉积.下面以一个空间力系为例,应用Matlab软件将力系的简化归纳为一个通用函数子程序,可以重复调用,力系中力的数目不受限制.

2.1 空间力系主矢、主矩的计算公式

如图1所示,假设一刚体上作用一空间力系(F1,F2,…,Fn),将力系中各力向任选的简化中心O简化.首先以O为原点建立空间直角坐标系oxyz,将力系中的各力用其在x、y、z轴上的投影表示为矢量形式，即Fi=Fixi+Fiyj+Fizk,其主矢、主矩的计算计算公式为[7]：

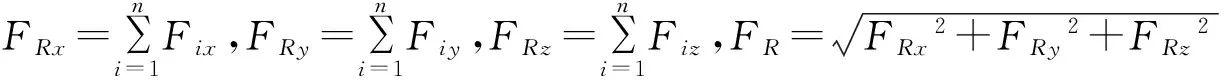
主矢的方向余弦：cos(FR,i)=FRx/FR,cos(FR,j)=FRy/FR,cos(FR,k)=FRz/FR

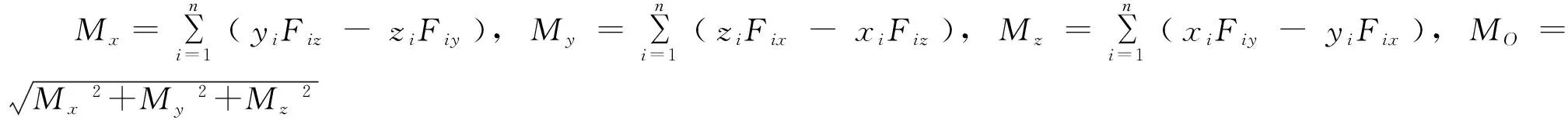
主矩的方向余弦：cos(Mo,i)=Mx/MO,cos(Mo,j)=My/MO,cos(Mo,k)=Mz/MO

2.2 空间力系主矢、主矩的计算举例

如图2所示构件力系的三力分别为F1= 350 N, F2= 400 N, F3=600 N,其作用线的位置如图所示,将此力系向原点O简化[7].

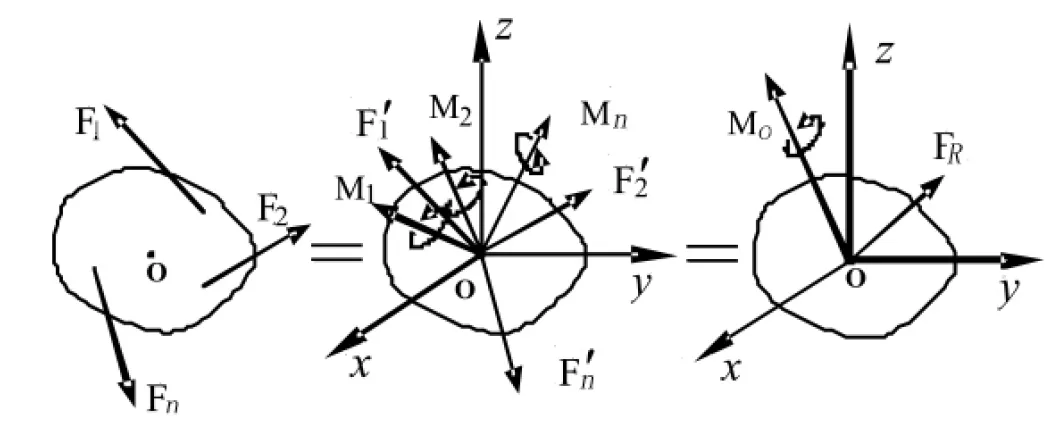
图1 空间力系的简化过程

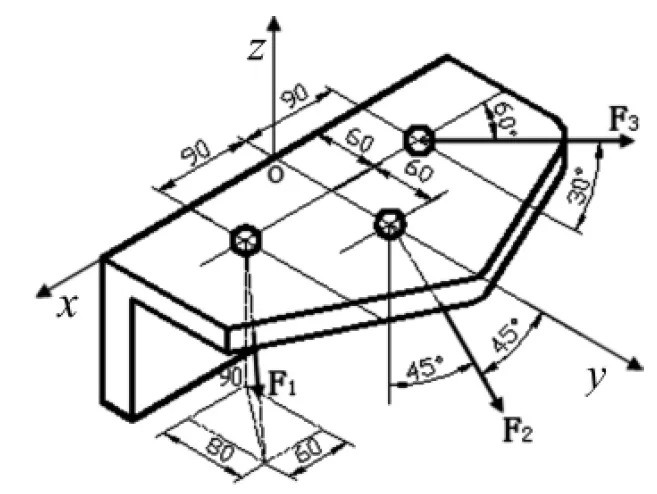
图2 空间力系简化实例

求解时首先整理已知力数据列成表1,用力在坐标轴x、y、z轴上的投影表示成矢量形式.

已知数据可以在运行程序时由键盘交互输入,也可以启动有关编辑程序或Matlab文本编辑器输入，以纯文本方式存盘为.m或.mat格式[6],调用力系简化子程序,直接访问Matlab工作空间中所有变量,运行程序得出简化结果(包括主矢和主矩的大小和方向角).Matlab力系简化函数程序如下,它的主要功能是实现空间力系的简化,对其他力系同样适用.

表1 空间力系已知数据

function lixijianhua(N1,F,r)

%N1为力系中已知力总数

%F、r分别为已知力矢、已知力作用点坐标矩阵

load N1-F-r.mat；

disp('空间一般力系简化结果:');

%计算主矢

S=sum(F(1:N1,1:3)); %计算合力投影矩阵

FR=sqrt(S(1)^2+S(2)^2+S(3)^2); %计算合力大小

disp(['主矢大小=',num2str(FR),'N']);

FRangles=acos(S/FR)*180/pi;

disp(['主矢方向角[α β γ]=

[',num2str(FRangles),']度'])；

%计算主矩

Mo=zeros(1,3); %主矩向量赋初值

for i=1:N1

Mo=Mo+cross(r(i,1:3),F(i,1:3));

end

disp(['主矩矢Mo=[',num2str(Mo),']N.mm']);

MoNum=norm(Mo);%计算主矩大小

Moangles=acos(Mo/MoNum)*180/pi;

disp(['主矩大小=',num2str(MoNum),'N.mm']);

disp(['主矩方向角[α β γ]=

[',num2str(Moangles),']度']);

运行程序得到结果如下：

主矢大小=1 144.225N

主矢方向角[α β γ]=[97.225 18 27.969 1 116.860 3]度

主矩矢Mo=[-47 989.384 9 21 072.389 -19 399.865 6]N.mm

主矩大小=55 887.220 6 N.mm

主矩方向角[α β γ]=[149.169 67.848 8 110.311 6]度

图3 空间力系平衡举例

3 Matlab用于力系的平衡

静力学的核心是平衡方程.空间力系作用下单个物体的静定问题有6个平衡方程,n个构件组成的物系可列出6n个独立的平衡方程,解6n个未知数.随构件数目的增多,线性方程组的数目也就越多.因此需要用到线性代数的知识,利用计算机求解. 运用Matlab语言,可以把复杂的线性方程组用矩阵的形式表示出来.一般可选用直接法和迭代法求解.直接法分为运算符求解和矩阵分解求解,通过对矩阵和Matlab相关函数的操作实现.

3.1 空间力系平衡计算举例

如图3(a)所示,装有两个带轮C和D的水平传动轴AB,支承于径向轴承A、B上,轮半径R1=200 mm,R2=250 mm,距离a=c=500 mm,b=1 000 mm.已知轮C上胶带拉力的方向成水平,其大小T2=2T1=5 kN；轮D上两边的胶带互相平行,并与铅垂线夹角α=30°,其拉力大小T3=2T4.不计轮和轴的重量,试求在平衡状态下胶带拉力T3、T4及轴承A、B的约束反力[9].

具体求解步骤如下：

(1)建立力学模型 取轴与轮整体系统为研究对象,建立坐标系oxyz,画出受力图如图3(b).

(2)建立数学模型 系统受空间力系的作用,根据受力图,静力平衡方程表示如下：

∑Fx=0,FAx+FBx+T1+T2+(T3+T4)sinα=0

∑Fz=0,FAz+FBz-(T3+T4)cosα=0

∑Mx(F)=0,FBz(a+b+c)-(T3+T4)cosα×(a+b)=0

∑My(F)=0, (T3-T4)R2+(T1-T2)R1=0

∑Mz(F)=0, -FBx(a+b+c)-(T1+T2)a-(T3+T4)sinα×(a+b)=0

T3=2T4

方程中包含轴承A、B的约束反力FAx、FAz、FBx、FBz及T3、T4共6个未知数,将已知力移到等式右边,整理为标准的矩阵方程AX=B的形式：

编制Matlab程序求解

clear;

R1=200;R2=250; a=500; b=500;

c=1000; alpha=30*pi/180; T1=2.5; T2=5;

A=[1 0 1 0 sin(alpha) sin(alpha);

0 1 0 1 -cos(alpha) -cos(alpha);

0 0 0 a+b+c -cos(alpha)*(a+b) -cos(alpha)*(a+b);

0 0 0 0 R2-R2;

0 0 -(a+b+c) 0 -sin(alpha)*(a+b)-sin(alpha)*(a+b);

0 0 0 0 1 -2 ];

B=[-T1-T2;0;0;(T2-T1)*R1;

(T1+T2)*a ; 0];

% [L,U]=lu(A); X=U(LB) %LU分解求解

X=AB;%矩阵除法求解

X=X';

%显示结果

disp(['[FAx FAz FBx FBz T3 T4]=[',num2str(X),'] [KN]'

程序运行结果如下：

[FAx FAz FBx FBz T3 T4]=[-6.375 1.299 -4.125 3.8971 4 2] [KN]

负值表明反力FAx、FBx的指向与图示方向相反.

5 结束语

Matlab语言具有强大的计算功能,编写简单、调试方便.借助于计算机辅助手段,拓宽了分析和处理工程实际问题的范围,把学生和设计人员从繁杂的数学计算和枯燥的编程中解放出来,使他们拥有更大的想象和发挥的空间，能够投入更多时间和精力去面向问题,专注于创造性的工作.

[1]陈怀琛.大学理工科要把“科学计算能力”当作一个重要培养目标[J].中国大学教学，2005,27(9):15-17.

[2]王国源.数值计算在理论力学中的应用[J].力学与实践，1990,12(1):62-63.

[3]邵小军,刘永寿,岳珠峰.谈工科理论力学教学中数学工具的应用[J].力学与实践，2007,29(5):68-69.

[4]曾德惠.基于Matlab实现函数逼近[J].现代电子技术，2009,32(18):141-143.

[5]管靖,彭芳麟,胡静,等.理论力学教学现代化-“理论力学计算机模拟实验”课程的探索[J].大学物理，2001,20(8):38-40.

[6]王正林,刘明.精通MATLAB7[M].北京：电子工业出版社，2006.

[7]哈尔滨工业大学理论力学教研室.理论力学(第6版)[M].北京：高等教育出版社，2002.

[8]赵秉新,郑来运.MATLAB在求解线性方程组中的多种应用[J].通化师范学院学报，2007,28(12):13-15.

[9]张毅.建筑力学(上)[M].北京：清华大学出版社，2006.