一类地下水问题的高次有限体积元方法

郭双冰,尹文双

(1.仰恩大学 数学系，福建 泉州 362014；2.湖北民族学院 理学院，湖北 恩施 445000)

地下水[1]由于其在人们生活和工业上的重要地位，正日益成为研究的热点问题[2,3].本文考虑如下的地下水一维模型[4]：

(1)

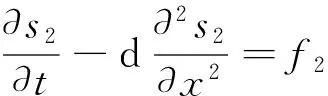
(2)

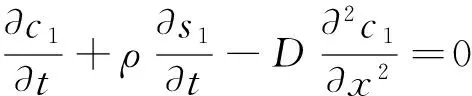
(3)

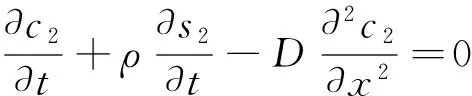
(4)

其中I=[a,b]有光滑边界的有界区域.J=(0,T].D>d>0为扩散系数，ρ>0为固体密度，它们都是常数.

(5)

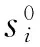
(6)

(7)

全文使用文献[5]中记号，为了得到最佳误差估计，作如下正则性假定：

式(1)～(7)有唯一解si,ci,i=1,2且si,ci∈H4(I),

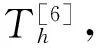
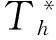
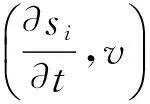
(8)

(9)

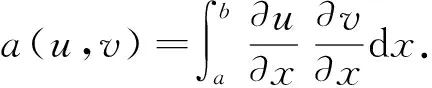
求解方程(1)～(4)的有限体积元格式为求s1,h,s2,h,c1,h,c2,h∈Uh使得：

∀vh∈Vh

(10)

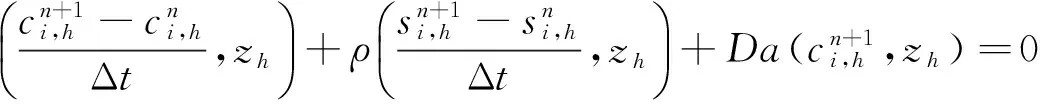
(11)

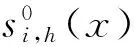
(12)

(13)

由式(8)～(11)，有下列误差方程：

(14)

(15)

误差估计前，假设时空剖分步长满足限制条件：Δt=ο(h4)，引入归纳假设：

(16)

(17)

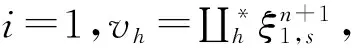
综合上述式子得到：

(18)

选择适当小的ε，将n从0到N-1求和，并将式子两端同乘以2Δt得到：

(19)

对ξ1,c,ξ2,s,ξ2,c用上述方法估计，则有：

(20)

(21)

(22)

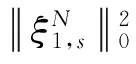
(23)

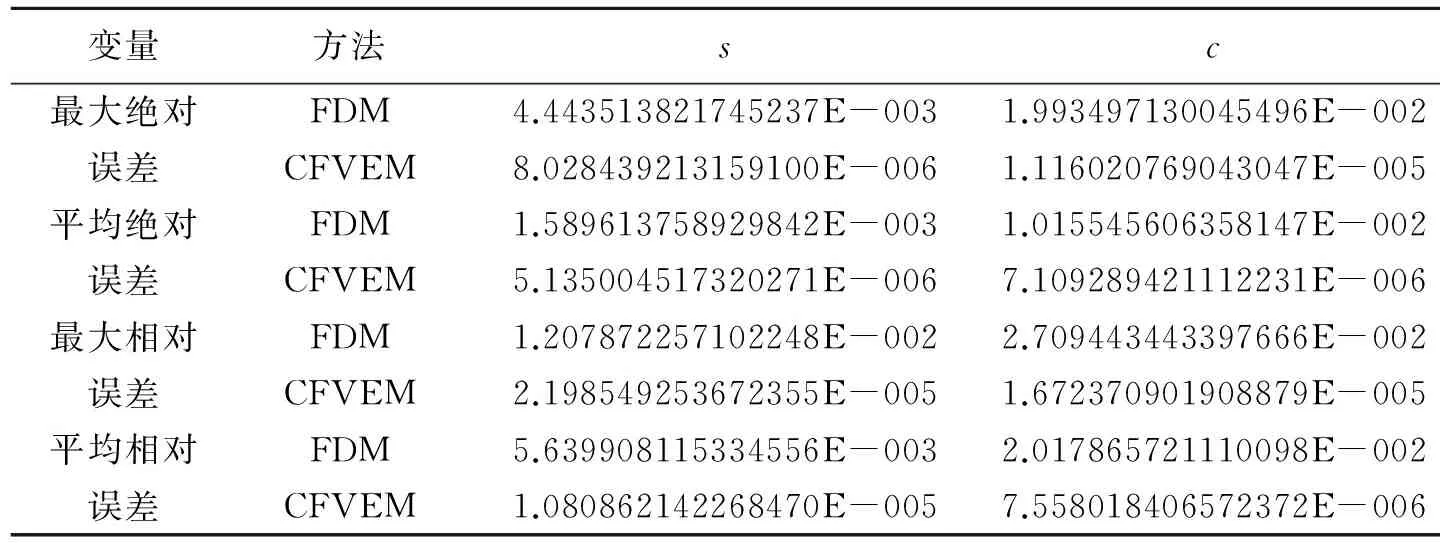
表1 T=1时,三次有限体积元方法与差分法的绝对误差与相对误差

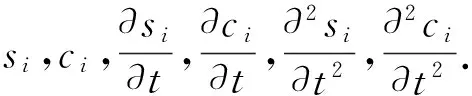
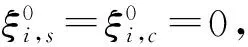
类似的，也有:

故假设(16)，(17)成立.这样由椭圆形问题Galerkin方法的结果[7,8]及式(23)，有以下定理：

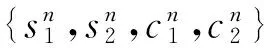
(24)

接下来，将用数值算例来证明格式(10)和(11)的有效性.考虑如下问题：

(25)

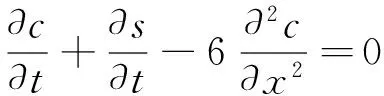
(26)

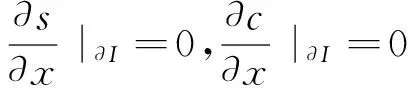
(27)

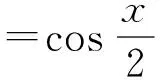
从表1中可以看出，当时间步长与空间步长满足合适比例时，CFVEM对,达到了理论分析上的精度.同时还可以看出CFVEM得到的数值结果的误差精度明显要好于FDM，说明了高次有限体积元格式的有效性.由此可见，数值实验能支持我们的理论.

致谢：对张志跃老师的悉心指导表示感谢！

[1]朱学愚.地下水水文学——中国现代科学全书·水文学[M].北京：中国环境科学出版社，2005.

[2]魏文清，马长明，魏文炳.地下水数值模拟的建模方法及应用[J].东北水利水电，2006,24(3)：25-28.

[3]张石峰，李茜，高佩玲.天然差分方法在地下水渗流问题中的应用[J].计算物理，2007,24(3)：307-312.

[4]朱学愚，谢春红.地下水运移模型[M].北京：中国建筑工业出版社，1990.

[5]Adams R.Sobolev Spaces[M].New york:Academic Press,1995.

[6]Ronghua, Chen Zhongyi,Wu Wei.Generalized difference methods for differential equations:Numerical analysis of finite volume methods[M].New York: Marcel Dekker,1999.

[7]Ciarlet P G.The Finite Element Methods for Elliptic Problems[M].Amsterdam:North-Holland,1978.

[8]Wheeler M F.A prioriL2error estimates for galerkin appeoximations to parabolic partial differential equation[J].SIAM J Numer Anal,1973(10):723-759.