基于动力有限元法的土石坝地震响应及稳定性分析

田贵川, 何江达, 肖明砾, 左林勇, 谢红强

(四川大学水利水电学院,四川成都 610065)

基于动力有限元法的土石坝地震响应及稳定性分析

田贵川, 何江达, 肖明砾, 左林勇, 谢红强

(四川大学水利水电学院,四川成都 610065)

地震对土石坝的危害已为工程人员所认识和重视,尤其是“5.12”汶川大地震后,西部地区土石坝在强地震作用下的抗震安全性已成为人们十分关心的重大问题。结合东风水库土石坝除险加固工程,基于动力分析中的等效线性模型,采用平面动力有限元法对土石坝进行了地震反应分析,揭示出不同地震动参数条件下坝体动应力、动位移、加速度、地震残余变形等的分布规律,对大坝的动力稳定性进行了评价,从而为除险加固设计提供了理论依据。

东风水库;土石坝;动力有限元;地震响应;稳定性

1 引 言

随着我国经济建设的迅速发展和西部大开发战略的实施,西部高坝大库的建设也越来越多。作为一种古老的水工建筑物,土石坝具有选材容易、造价低、结构简单、抗震性能好等特点,因而在世界范围内被广泛采用,也成为西部水电工程选择的主要坝型之一。然而,西部地区地形地质条件复杂,地震频繁、强度大,这些土石坝在强地震作用下的安全性如何是人们十分关心的重大问题。因而,土石坝抗震研究工作的迫切性和重要性越来越突出。

地震灾害作为一种严重的自然灾害,一旦发生便会带来惨重的损失。我国地域广阔,地震频繁而强烈。近几十年已发生过多次灾害性的大地震,如1966年邢台地震,1970年通海地震,1975年海城地震,1976年唐山地震等。尤其是在“5.12”汶川大地震后,位于西部强震区的土石坝不可避免地受到强地震的作用,其抗震安全性已成为人们普遍关注的关键技术问题。大量工程实践表明:地震的危害主要表现为永久变形和不均匀变形引起的裂缝;地震动力反应造成较大的动应力和动应变,从而降低坝体的稳定性;在坝体和坝基存在可液化性砂土时,地震过程中由于产生了较大的超静孔隙水压力,砂土可能产生液化,进而严重威胁工程的安全以及人民群众的生命财产。

目前,土石坝抗震稳定性分析主要采用拟静力法,该方法既未考虑地震特性,如振动频率、次数和地震持续时间等,又未考虑坝体材料动力性质和阻尼性质等,因而无法反映大坝在地震时的反应特性;采用有限元法进行土石坝地震动力反应分析,能够评价地震动力反应程度,计算地震永久变形的大小,得出坝内动应力应变和动孔隙水压力的分布,对存在液化土的情况进行液化可能性判别,并结合动力分析结果进行坝坡稳定性分析。对于一些重要工程、高坝和坝体或坝基中存在可液化性土的工程,规范规定必须采用有限元法进行动力分析。

鉴于“5.12”汶川大地震后部分水库大坝受到不同程度的影响,笔者以西部强震区典型土石坝工程——云南省玉溪东风水库大坝为研究对象,结合东风水库坝址区地形地质条件,采用非线性动力有限元法对心墙土石坝进行了地震反应分析,揭示了坝体及坝体的动应力、动应变分布规律,对土石坝的抗震安全性进行了评价。

2 土石坝非线性动力分析理论

地震荷载是一种非等幅等周期的不规则荷载。在一次地震动历程中,土石坝坝基及坝体料将经历数十次甚至上百次卸载和再加载的过程,并且它们之间是无规律可循的。为了解决分析的困难,比较常用的方法是应用Mashing规则,制定一个应力～应变关系的骨架曲线,衍生出双线性,粘弹性和弹塑性等多种模式的本构模型。

等效线性模型因其具有概念明确,应用方便等优点,在有限元动力计算中得到了广泛的运用,比如Hardin-Drnevich双曲线本构模型。等效线性模型是把土视为粘弹性体,采用等效弹性弹模量E(或G)和等效阻尼比λ这两个参数来反映土动应力——动应变关系的两个基本特征:非线性与滞后性,并将模量与阻尼比均表示为动应变幅的函数。

2.1 等效线性剪切模量

Hardin等人由试验得出了土在周期荷载作用下的应力应变骨干曲线为双曲线型(图1),其表达式可写为:

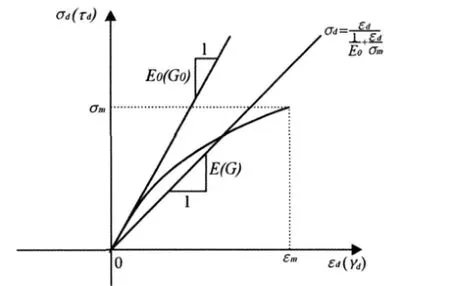
图1 动应力应变双曲线关系示意图

式中 G0为起始剪切模量;τy为最大动剪应力。将G0坡度线与τy水平线的交点横坐标称为参考应变γf,则γf=τy/G0。可得:

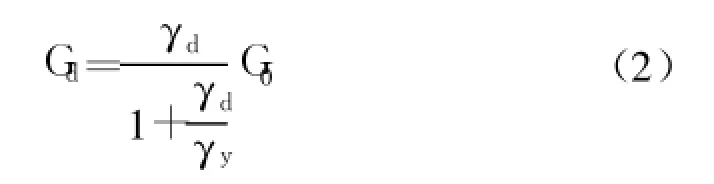
可见,只要根据试验曲线确定了G0和τy,即可求出相应于任意动剪应变γd的剪切弹模Gd。G0和τy可由动单剪试验求得,或者利用Hardin等人提出的一些经验公式。笔者选用了式(3):

式中 σ'0为平均有效应力;(k2)max为计算参数; τy近似根据莫尔-库仑准则求得。

2.2 等效阻尼比

Hardin等人从应力应变滞回圈的几何特征出发,假定剪切模量G和阻尼比D之间存在一种简单的关系,列出了D的计算模式。图2为典型应力应变滞回圈。试验表明:卸载曲线起始坡度总是等于或接近于G0(是of//bc),而与应变幅大小无关。同时,图2中阴影部分面积与三角形Δabc的面积之比变化很小,可假定等于常数α0。

图2 剪应力-剪应变关系图

Seed和Idriss也对各家测得的阻尼比进行了综合分析,可以根据试验资料相应的进行选取。笔者在报告中选用式(4)进行了计算。

式中 λmax为最大阻尼比,可根据试验确定。Hardin等人得出了以下经验公式:

式中 N为循环加载次数。

2.3 坝体动力残余变形分析

地震荷载在坝体内各部位所产生的循环剪切作用使得土体变软,模量衰减,从而使坝体发生不可恢复的永久变形,以此作为出发点的软化模量法就是由地震前的初始模量、震动结束后的软化模量分别进行静力分析,所求得的位移之差即可作为坝体残余变形。

计算坝体永久变形的软化模量法的基本概念是震动作用的主要效果使土变软,模量降低,因而产生永久变形。假定土体在震后的应力～应变关系仍然符合Duncan-Chang双曲线关系,且震前、震后土体单元应力状态不变,但应变在原始初始应变εi的基础上增加了震动残余应变εd,则由应力协调条件可推出:

式中 下标i表示震动前;ip表示震动后。

现Ep=(σ1-σ3)i/εp,并考虑地震持续周期较短,土体不排水,则震后泊松比μip等于:

由式(6)、(7)计算出各单元震后的Eip、μip,将其代入静力平衡方程,按一次加载线弹性计算软化后的坝体变形μip考虑,则坝体的永久变形即为震前、震后变形之差,即坝体震后永久残余变形:

2.4 抗滑稳定校核

为了校核坝体上、下游堆石坡面的局部抗滑稳定性,采用式(9)计算其安全系数:

式中 g为重力加速度;φ为堆石内摩擦角;α为坡角;amax为坝面特征点历时最大加速度。

2.5 土石坝动力有限元计算步骤

根据上述理论,土石坝动力有限元分析的步骤如下:

(1)计算初始应力;

(2)将地震波分为若干时段(每时段=0.02 s),对每个时段的各单元循环并组集质量矩阵[M]和刚度矩阵[K]进行计算,其中各单元非线性常数(Gd、λ)由质量矩阵刚度阵

(3)振型分解求出第一阶频率,计算瑞雷阻尼系数:α=λdω;β=λd/ω;

(4)将时段分为50～100步,用Newmark法积分,得出时步节点位移、速度和加速度、动剪应变和动剪应力;

(5)从时程中找出(λd)max;

(6)由新的λd对各单元重新确定新的Gd、λ,重复(2)～(5)步直到前后两次λd之差小于允许值;

(7)进行下一时段的运算,直至地震结束。

3 土石坝动力有限元模型

东风水库工程位于玉溪市红塔区东北部沙头村南盘江一级支流曲江上游河段,属中型水库工程。拦河大坝为粘土心墙土石坝,坝顶高程为1 684.24 m,坝高47.41m,坝顶长450 m,坝顶宽9.8 m。由于心墙防渗体部位填筑质量差,坝体压实度低,力学指标低,上、下游坝壳土料填筑质量差,坝基下F5断裂带宽达126～130 m,坝基稳定性差,大坝存在较大的安全隐患,尤其是在“5.12”汶川大地震后,其抗震稳定性问题显得十分突出。

3.1 计算模型

选取河床坝段最大横剖面为研究对象,计算模型坝踵以上及坝趾以下各取2～3倍坝高,顺河向距离为200m,坝基深度取约2倍坝高,底部向下取至高程1 530 m,向上取至坝顶,铅直向高度为154.2 m。对计算范围内的坝体及坝基采用4节点平面等参单元进行离散;在防渗墙与坝基等凝聚力差别大的材料之间设置接触单元,以模拟两者的接触特性。整个计算范围共离散单元总数1 040个,节点总数1 008个,有限元模型见图3。

3.2 计算参数

图3 平面有限元计算网络图

土体在静力状态下的初始静应力对地震作用下土石坝的动力反应有较大影响,本次有限元首先采用静力模型计算大坝及坝基的初始应力场,再采用动力本构模型进行动力分析。在静力计算中,土体本构关系采用邓肯-张8参数非线性弹性模型,选取了粘土心墙、坝壳料、堆石棱体、河床冲积层、F5断裂、全强风化岩体、基岩等7种材料,各种材料力学参数均采用静力试验参数(表1)。

采用等价线性法进行动力分析时,土的动力特性可用微幅应变水平下的最大剪切模量Gmax,即Gm=Gmax=Km(σ'0)n与剪切模量G及阻尼比ξ随剪应变大小γ的变化规律来描述,Km、n为经验常数。表2给出了基于动三轴试验所确定的部分材料动力计算参数。

3.3 输入地震参数

根据云南省地震工程研究院提供的坝址区地震危险性分析报告,东风水库坝址区的地震基本烈度为Ⅷ度,其中50年超越周期10%的峰值加速度场地地表峰值加速度amax=2.230 9m/s2、特征周期Tg=0.35 s、放大系数β=2.25,水平向设计地震加速度代表值ah=0.227。针对坝体而言,由于地震源传来的地震波方向存在一定的随机性,二维有限元计算输入两个方向(顺河向和铅直向),动力计算中采用的地震为50年超越概率为10%的人工合成加速度曲线,铅直向为顺河向地震波的2/3(图4)。

表1 坝体及坝基料静力计算参数表(Duncan-Chang模型)

表2 坝体坝基材料动力计算参数表

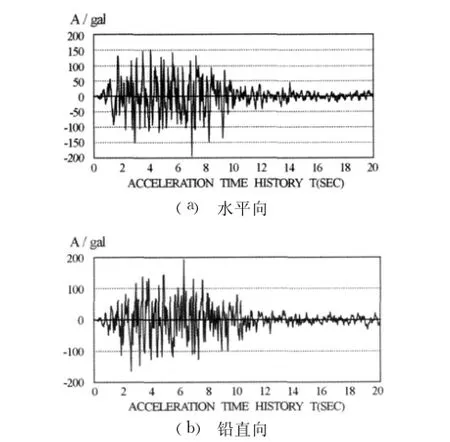
图4 50年超越概率10%基岩加速度时程示意图

4 计算成果与分析

根据《碾压式土石坝设计规范》(SL274-2001)的规定,本次静力计算拟定正常工况(正常蓄水位稳渗期、设计洪水位稳渗期、死水位稳渗期)和非常工况Ⅰ(校核洪水位稳渗期)进行有限元分析,计算中均采用有效应力。限于篇幅,文中仅列出正常蓄水位稳渗期的相关成果。

4.1 加速度反应

从坝体加速的历时分布看(图5):幅值较大的时间出现在强震阶段(2.0～7.4 s)。但由于阻尼作用,加速度与输入加速度并不同步,存在一定的滞后效应,且越靠近坝顶越明显,加速度反应的最大时段大约为6.0～8.0 s,铅直向速度与加速度的滞后效应不明显,基本与输入加速度同步。最大水平加速度和铅直加速度均出现在坝体顶部,量值分别为2.612 m/s2和1.874 m/s2,水平放大系数为2.170,铅直放大系数为2.264。

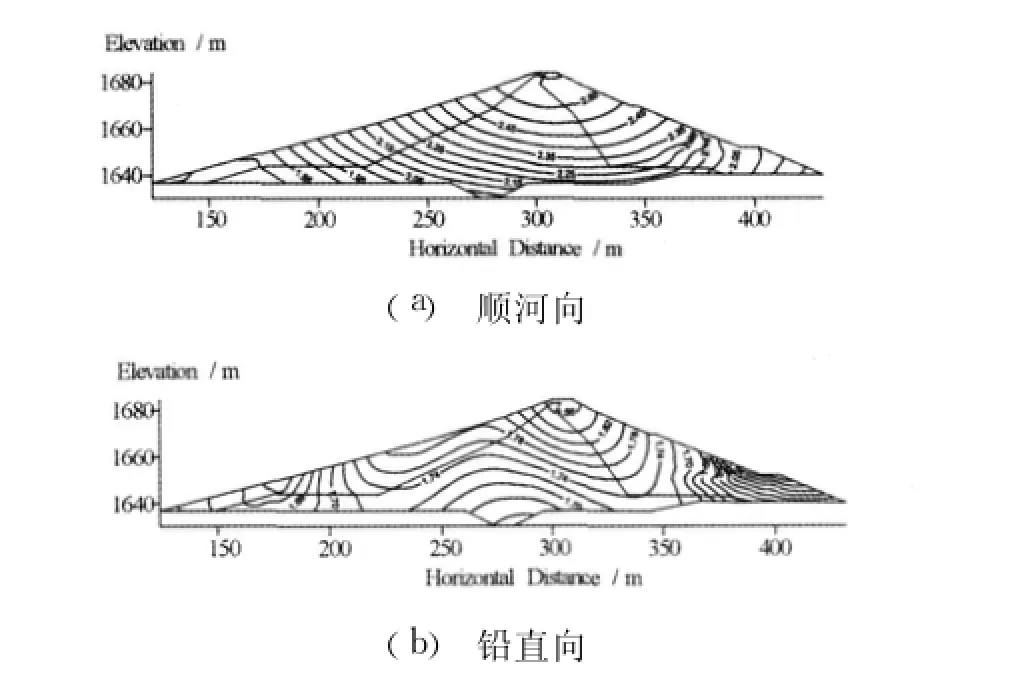
图5 坝体最大加速度等值线图

4.2 坝体动位移反应

从坝体动位移的历时分布看(图6):幅值较大的时间出现在强震阶段(2.0～7.4 s),同样存在“滞后现象”,水平向动位移滞后效应较铅直向更为明显;水平动位移反应的最大时段大约在6.0～8.0 s之间,铅直动位移的最大反应时段约为4.0～7.0 s(图5)。最大动位移出现在坝顶,其中历时最大水平动位移约15.77 cm,历时铅直最大动位移值约4.77 cm;同一高程下,水平动位移及铅直动位移均随水平深度的增加而递减,即坝壳料的动位移较防渗体的动位移要大。

图6 坝体最大动位移等值线图

4.3 坝体动应力反应

主应力量值出现在输入地震波的强震阶段(7.0～9.0 s),大主应力σ1、小主应力σ3及等效剪应力τeqv均随坝高的增加而呈递减趋势。同一高程主应力及剪应力沿坝轴线基本呈对称分布且随水平深度的增加而增大;从坝料分区的动应力分布看,防渗体中的动应力较之坝壳料要大;坝体总体处于压应力状态,但在上下游坝壳料中下部高程浅表层及堆石棱体内出现一定的拉应力区域;坝体最大动应力的最大值:主压应力为0.98 MPa,主拉应力为-0.25 MPa(图7)。

4.4 坝体永久变形

坝体的永久变形以沉降变形为主(图8),无论水平永久变形还是铅直永久变形,坝体上游坝壳料的永久变形较下游坝壳料大,防渗体永久变形最小;最大水平残余变形发生在上游坝壳料表面,量值约0.8 cm,最大铅直残余变形(地震沉陷)发生在坝顶,量值约17.0 cm。

4.5 上下游坝坡局部抗滑稳定性

局部稳定性计算成果表明:在超越概率10%的情况下,上下游坝面的浅表层动抗滑稳定安全系数均大于1.0,且随高程的降低逐渐增大,同时,上游坝面的抗滑稳定安全系数大于下游坝面,坝面不存在浅层失稳风险。

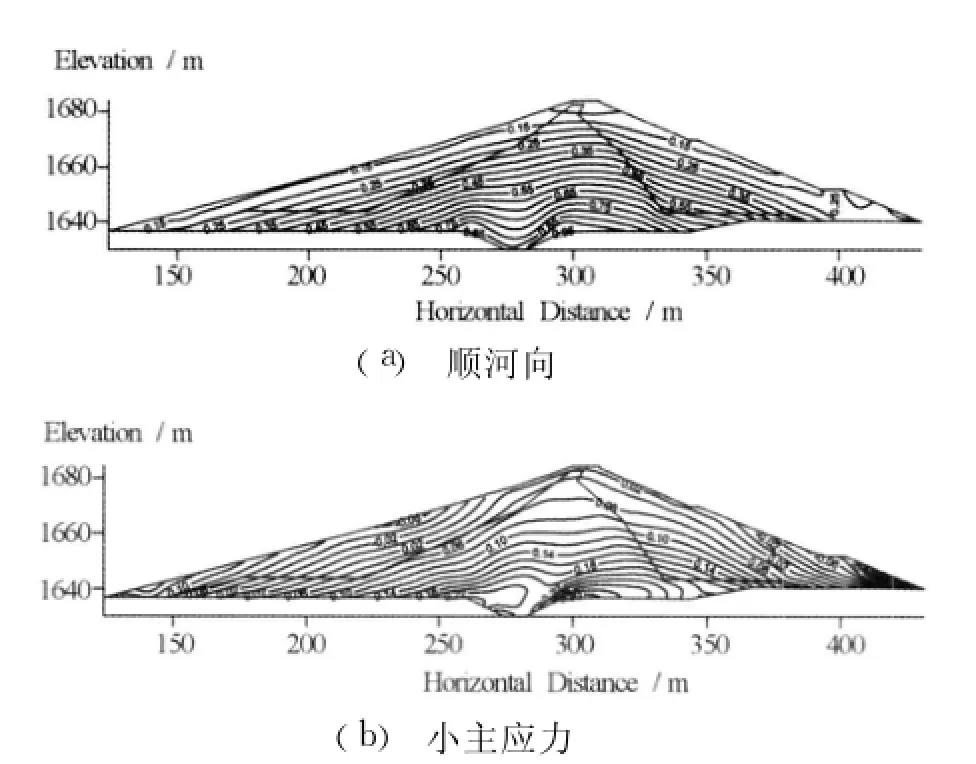
图7 坝体最大动应力等值线图

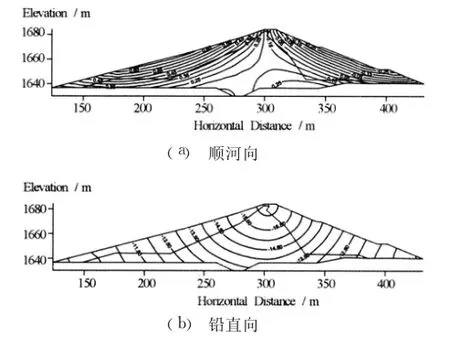
图8 坝体永久变形等值线图

5 结 论

土石坝的抗震安全评价是一个复杂的岩土工程问题,涉及到对未来可能产生的地震活动性进行评价,坝体及地基材料在静力、动力条件下物理性质和力学性能确定等复杂问题。笔者结合东风水库粘土心墙土石坝工程,通过平面动力有限元法,对坝体及坝基的动力响应进行了研究,并从坝体动位移、动应力、加速度、地震残余变形等角度出发,对大坝的抗震稳定性进行了评价,得出了以下结论:

(1)防渗体及上下游堆石区整体应力水平较低,上下游坝壳料中上部高程浅层抗滑稳定安全系数均大于1.0,不会产生局部滚石危险,但上下游堆石区坡脚附近浅表层存在一定的拉应力区。

(2)由于存在阻尼作用,动位移和输入加速度并不同步,动位移、加速度、动应力反应存在明显的“滞后现象”,且越靠近坝顶滞后效应越明显,水平向动位移滞后效应较铅直向更为明显。

(3)最大加速度一般发生在坝顶或坝面,顶部振动的“鞭稍”效应较为明显,最大动位移也发生在坝顶部位,上下游坝脚前表层出现拉应力区,因此,坝体的地震破坏也是先从坝顶或坝面开始。

鉴于地震作用下上、下游坝壳料坡脚附近存在一定的拉应力区,为了进一步提高大坝的抗震能力,建议对上游坡脚进行抛石压脚,下游坡脚设堆石压重体等予以加固。

[1] 谢定义.土动力学[M].西安:西安交通大学出版社,1988.

[2] 顾淦臣.土石坝地震工程[M].南京:河海大学出版社, 1989.

[3] 熊美林,周 伟.埃塞俄比亚KESEM土石坝动力分析[J].湖北水力发电,2008,3(3):18-22.

[4] 韩凤霞.土石坝动力反应分析[J].山东电力技术,2002, 125(3):67-68.

[5] 徐志英.土石坝动力分析的现状及其发展趋势[J].水利水电科技进展,1982,2(3):113-124.

(责任编辑:李燕辉)

TV 641;TV31

B

1001-2184(2010)01-0088-06

20009-01-17

田贵川(1983-),男,贵州贵阳人,在读硕士研究生,从事岩土工程数值模拟研究;

何江达(1961-),男,四川达州人,教授,博士生导师,博士,从事岩土工程及水工结构的教学与科研工作;

肖明砾(1981-),男,四川成都人,讲师,在读博士研究生,从事岩土工程及水工结构的教学与科研工作;

左林勇(1983-),男,四川眉山人,在读硕士研究生,从事岩土工程数值模拟研究;

谢红强(1976-),男,四川成都人,讲师,博士,从事岩土工程及水工结构的教学与科研工作.