基于棋盘覆盖的文件加密技术

王防修,周 康

(武汉工业学院数理科学系,湖北武汉 430023)

随着网络化的普及,信息的传播和共享变得更加方便,同时,信息的安全性受到极大威胁.因此,尽可能地保护信息的安全是一项艰巨的任务.目前,常用的保护信息的方法就是对文件加密[1].由于传统加密算法是公开的,根据现有计算机的计算能力,如果已知加密算法,一般都能够借助计算机比较快地得到加密的密匙.由于棋盘覆盖的特殊性和灵活性,使得将其用于文件加密,可以大大增强信息的安全性.即使将该算法公之于众,想通过密文和部分明文得到密匙几乎是一件不可能的事情.

1 棋盘覆盖[2]的工作原理

定义 1在一个 2k×2k个方格组成的棋盘中,如果恰有一个方格与其它方格不同,则称该方格为一特殊方格,且称该棋盘为一特殊棋盘.

显然,特殊方格在棋盘上出现的位置有 4k种情形.因此,对∀k≥0,有 4k种不同的特殊棋盘.

定义 2所谓棋盘覆盖,是指要用如图1所示的 4种不同形态的L型骨牌覆盖一个给定的特殊棋盘上除特殊方格以外的所有方格,且任何两个 L型骨牌不得重叠覆盖.

图14种不同形态的 L型骨牌

因此,在任何一个 2k×2k的棋盘覆盖中,用到的 L型骨牌个数恰为 (4k-1)/3.

1.1 用分治法对一个特殊棋盘进行覆盖的原理

(1)设 k＞0,将 2k×2k棋盘分割为 4个 2k-1×2k-1的子棋盘;(2)特殊方格必位于 4个较小子棋盘之一中,其余 3个子棋盘中无特殊方格.为了将这 3个无特殊方格的子棋盘转化为特殊棋盘,我们可以用一个L型骨牌覆盖这 3个较小子棋盘的会合处,这 3个子棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格,从而将原问题转化为 4个较小规模的棋盘覆盖问题;(3)递归地使用这种分割,直至棋盘简化为 1×1棋盘.

1.2 棋盘覆盖实例

设棋盘覆盖的递归算法如下.

先将棋盘划分为四个大小相同的子棋盘,为了叙述方便,不妨将这四个子棋盘分别称之为：左上角子棋盘,右上角子棋盘,左下角子棋盘,右下角子棋盘.具体如图2所示.

图2 棋盘分割

然后按递归覆盖左上角子棋盘,递归覆盖右上角子棋盘,递归覆盖左下角子棋盘,递归覆盖右下角子棋盘的顺序覆盖整个棋盘.

当 k=3,则得到如图3所示的不同特殊棋盘的棋盘覆盖.

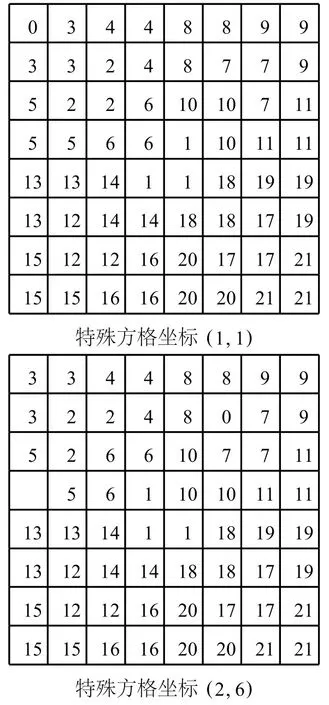
图3 k=3时的两种不同特殊方格的棋盘覆盖

从结果可以看出,不同特殊棋盘上相应的格子里有很多内容是相同的.

1.3 递归算法的改进

上述两种不同特殊方格的棋盘覆盖的内容之所以大同小异,会不会是由于采用相同的递归算法造成的呢?因此,不妨按递归覆盖右上角子棋盘,递归覆盖左上角子棋盘,递归覆盖右下角子棋盘,递归覆盖左下角子棋盘的顺序覆盖整个棋盘,则得到如图4所示的结果.

图4 特殊方格坐标 (1,1)所对应的棋盘覆盖

与图3中特殊方格坐标 (1,1)所对应的棋盘覆盖相比较,棋盘中的内容有很大差别.正是因为这种差别,后面所说的加密算法就是充分利用这一点来达到目的的.

2 用棋盘覆盖实现文件加密的原理

2.1 棋盘大小的选择

所谓棋盘大小的选择,实质上就是 k值的合理选择.为了实现文件到棋盘的单射[3],棋盘格子的个数至少必须等于文件的大小.只有当文件的大小为 4k(其中 k为整数),棋盘的大小才与文件的大小相一致.事实上,文件的大小往往不可能为 4k.因此,棋盘的大小一般要比文件大.虽然只要棋盘比文件大,都可以实现文件到棋盘的单射,但考虑到大的棋盘所占的内存空间也越大,因此我们一般选择比相应文件要大的较小棋盘.

假设某个待加密的文件的大小为 filesize,那么棋盘的大小为 4k,其中 k=min{n|4n≥filesize,n∈Z}.

2.2 根据棋盘对文件进行加密的过程

为了简单起见,我们不妨对文件进行逐个字节加密.具体的加密过程：(1)测量出要加密的文件的大小为 filesize;(2)顺序读出文件的内容;(3)假设读出文件的第 i个字节的内容为 ch,则可以通过 i计算出棋盘上具体的格子位置,具体方法是

然后通过 ch=ch⊗board[row][col]mod256实现 ch的加密,其中⊗表示加密运算,board[i][j]表示棋盘上第 i行和第 j列的格子的骨牌号;(4)将加密后的密文依次写入密文文件中.

2.3 根据棋盘对文件进行解密的过程

跟上述的加密过程相反,我们必须对密文进行逐个字节解密.具体的解密过程：(1)测量出要解密的文件的大小为 filesize;(2)顺序读出文件的内容;(3)假设读出文件的第 i个字节的内容为 ch,则可以通过 i计算出棋盘上具体的格子位置,具体方法是

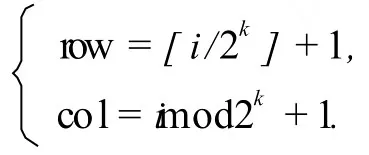
然后通过 ch=ch⊕board[row][col]mod256实现 ch的解密,其中⊕表示解密运算,board[i][j]表示棋盘上第 i行和第 j列的格子的骨牌号;(4)将解密后的明文依次写入明文文件中.

3 密匙分析

如果获得通过上述方法加密的密文和部分密文所对应的明文[4],同时又知道加密算法,那么要得到密匙是一件很容易的事情.首先,通过密文文件的大小,可以计算出棋盘的大小.如果知道该棋盘的特殊方格所处的位置,则该特殊棋盘的覆盖唯一确定.因此,密文对应棋盘的特殊方格所处的行号和列号就是文件加密的密匙.由加密与解密的过程知道,此处的加密算法是对称性的,即加密与解密的密匙相同.如果棋盘大小为 4k,则特殊方格所处的位置有4k种可能.因此,只要知道两个字节的密文所对应的明文,则只要用解密算法最多尝试执行 4k次,就可以得到密匙.

通过以上分析,说明仅仅用棋盘覆盖还不足以显示它在文件加密中的威力.必须对现有算法加以改进,才能真正体现棋盘覆盖对文件加密的优点.

4 算法改进

前面的算法之所以需要改进,就是通过计算机算出它的密匙比较容易.出现这种情况原因有三：(1)棋盘的大小可以通过文件的大小计算出来;(2)字符加密的对象可以通过字符在文件中所处的位置计算出来;(3)不同字符与棋盘中不同格子的骨牌号进行加密.因此,可以通过下列方法增加密文解密的难度.

4.1 棋盘大小不受文件大小的限制

为了克服通过文件能够计算出棋盘大小的缺点,有必要对其进行改进.实际上,只要满足 2k×2k个格子的棋盘都可以,只不过此时文件中的字符与棋盘的格子之间不存在单射关系而已,但这并不影响文件的加密与解密.

因此,如果无法知道 k的具体值,那么就无法对密文进行解密.显然,这里的 k就是密匙的一部分.

4.2 文件中不同字符加密对象的选择

前面关于每个字符的加密对象完全是由该字符在文件中所处的位置决定的,文件中不同位置的字符对应棋盘中的不同格子,因此棋盘必须比文件大.而改进后的棋盘可能比文件大也可能比文件小,当棋盘比文件小时,必然存在文件中不同位置的字符被棋盘中同一格子的骨牌号加密.为了能够兼容任意大小的棋盘,必须对字符的加密对象作出选择,使得在解密时也能够选择与加密相同的解密对象.

在具体为文件中的某个字符选择加密对象时,我们可以通过随机函数来实现随机选择棋盘中对应的某个格子.

由仿射密码[5]的原理,我们可以将随机函数定义为：e(x)=(ax+b)modm,其中 a,b∈Zm,mod表示取余运算.

因此,为了给当前的字符选择棋盘中具体的格子来进行加密,可以通过下列迭代函数组实现随机选择.

随着 a1,b1,a2,b2的值以及 x,y初始值的不同,那么在加密过程中选择的加密对象就会有很大的不同.此时的加密过函数为：

显然,此时的密匙由 a1,a2,b1,b2,x,y,k组成.

4.3 棋盘递归覆盖算法的选择

由前面的分析可以知道,对于相同大小的棋盘,即使特殊方格相同,如果采用不同递归覆盖算法,那么棋盘中的骨牌号有很大差别.总共有 24种递归覆盖算法,具体加密时,只需选择其中的一种,只有知道是哪一种递归覆盖算法,才能够对密文进行解密.

5 算法分析

通过前面的分析,棋盘覆盖有 24种算法,而参数 x1,y1,a1,b1,a2,b2每个都有 232种可能.此外,k有 32种可能,而特殊方格有 4k种情形.因此,密匙空间[6]的大小为 24×232×232×232×232×232×232×32×4k=3×2200+2k,即可供选择的密匙有 3×2200+2k个.实践表明,如果知道加密算法,且知道部分密文对应的明文,要从现有的计算机解密出密匙是不可能的.因此,用此种方法对文件进行加密可以大大增强文件的安全性.

6 结束语

本文通过对棋盘覆盖的介绍,从原理上说明将其用于文件加密的可行性.虽然我们在此处采用的是对称性加密,但由于密匙空间太大,非法用户很难通过计算机计算出加密的密匙.实践表明,应用本文所述方法对文件进行加密,可以大大增强信息传输的安全性.

[1] 阚晓初.电子商务安全中的数据加密技术[J].计算机教育,2007(18).

[2] 王晓东.计算机算法设计与分析[M].北京：电子工业出版社,2006.

[3] 吴海涛.数据加密技术的研究与探讨[J].科技咨询,2007(24).

[4] 陈运.信息加密原理[M].成都：电子科技大学出版社,1990.

[5] 张周.我国企业开始重视网络安全[J].计算机世界 (A9版),2000(3).

[6] 卢开澄.计算机密码学 (第三版)[M].北京：清华大学出版社,2003.