基于李雅普诺夫指数的矿产资源评价模型的建立
韩兆红,吴燕冈,徐 兵,赵玉岩
(1.吉林大学 地球探测科学与技术学院,吉林长春 130026 2.吉林工程技术师范学院 应用理学院,吉林长春 130052)
0 前言
矿产资源评价是对矿产资源空间分布的属性、性态、程度、规模、数量、质量、位置等特征变量,采用相应的数学、地质、计算技术等方法进行的评价,即以地质学理论和方法为指导,通过信息的提取方法揭示了矿产资源的属性特征。因此,其核心问题可以归结为信息处理的理论、方法、技术同地质理论的结合。随着科学技术的发展,特别是非线性理论的发展,以混沌、分形为主要标志的非线性资源评价的评价方法,正日益受到重视。作者在本文中,通过对非线性理论在成矿中的机理,以及矿床分布特点的讨论,建立了以李雅普诺夫指数为基础的资源评价方法的数学模型。
1 李雅普诺夫指数法原理
混沌运动最重要的特征,就是其对初始条件的极度敏感性。在混沌系统中不可能对系统的状态进行长期的预测,这是因为在初始状态的微小不确定性将会按指数速度迅速扩大。在非混沌系统中,相互靠近的轨迹,要么是指数的收敛,要么慢于指数速度的发散(最坏情况),至少在理论上,长期预测是可能的。这种轨迹收敛或发散的比率,称为李雅普诺夫指数(Lyapunov exponent)。一般情况下,李雅普诺夫指数的数目和相空间的维数一样多,每个指数描述一类相互靠近的轨迹对行为。对于维数大于1的系统,存在李雅普诺夫指数的集合,称为李雅普诺夫指数谱。
常用李雅普诺夫指数计算方法,大体上分属于二大类:Wolf方法和Jacobian方法。
(1)Wolf方法适用于时间序列无噪声,切空间中小向量的演变高度非线性。
(2)Jacobian方法适用于时间序列噪声大,切空间中小向量的演变接近线性。
G.Barana和I.Tsuda曾提出一种新的P—范数算法,在Wolf方法和Jacobian方法之间架起了桥梁。但P—范数的选取和计算复杂,实际操作困难。M.T.Rosetein、J.J.Collins和G.J.De luca提出的一种小数据量的计算方法,操作起来比较方便,而且具有①对小数据组比较可靠;②计算量较小;③相对易操作优点。
2 李雅普诺夫指数与成矿的关系
申维在《矿化富集的耗散结构研究》一文中,把Logistic方程中μ和成矿关系进行了讨论;於崇文、徐兵对成矿的混沌性进行了研究。基于此有:①在李雅普诺夫指数λ<0的方向,相体积收缩,运动稳定,且对初始条件不敏感,在此区间上无矿;②在λ>0的方向轨道迅速分离,长时间行为对初始条件敏感,运动呈混沌状态,再次区间上成矿;③λ=0对应于稳定边界,属于一种临界情况,这种分类方法应根据相应的矿床进行地质的认识。
3 李雅普诺夫指数法在资源评价中的应用方法
由于李雅普诺夫指数有一个特殊意义的含义,即代表数据的分离程度,那么就可以利用数据计算出相应的李雅普诺夫指数,由此评价形成了各种评价方法。
作者在本文讨论的问题是已知某区域的信息,评价该区域中的区域S的信息,这需要二部分,一部分是对S内的信息进一步认识,同时更重要的是认识整个研究区的信息。而整个研究区的认识是基于原来小区域的信息,首先研究它的信息,即地质学上的信息如构造带、断裂、回旋、展理、岩层、岩性等。在地球化学方面,如元素的分布含量变化,变化的特征以及采样的程度等。在地球物理方面,如重力、航磁等的特征,而这些特征有些是定量的,有些是难以定量的,甚至就是定性的,如岩性是难以量化的,这样对于信息的要求是多方面的统一体。而这些信息在一个成矿区域内,是如何表现出其特征,它如何扩展到整个区域的研究,这些都有待于更深刻的认识。
4 地质异常变量的选择方法
在资源评价时,通常在研究程度较高,或有一定的地质研究工作的地区,选择一些已知矿床作为标准对象。或选择一些地质条件已知的地区,作为控制区或模型区。所有这些标准对象及控制区,都是作为定量类比的标准,然后用未知区与其进行对比,从而评价未知区的资源潜力。因此,资源评价预测的效果,一方面取决于所建立的模型是否正确,另一方面取决于对类比对象相似程度的把握。通常采取以下的选择方法:
(1)在地质异常致矿概念模型基础上选择变量。
(2)以地质异常体为单元进行综合变量的选择。
(3)通过已知矿异常单元成矿特征的横向对比,选择定位预测变量。
(4)在区域综合地质致矿异常图编制的基础上选择变量。
5 数学模型的建立方法
下面将通过已知区域的信息评价预测区的特征和属性,我们在某研究区内共划分矿床n+1处,在对已知n个区域的资料进行研究的基础上,提取了综合信息地质变量。通过这些地质变量(自变量),建立如下数学模型。
设已知区(模型单元)有n个,评价区有m个,对已知区的李雅普诺夫指数,λ1、...、λn计算评价区的李雅普诺夫指数,写成线性表达式为

其中 xij表示第i个模型单元的地质变量。
由这个方程组利用最小二乘法,可以识别出参数^aj,并由此得到相应的方程,对于评价区的评价进行回代,即可以确定出相应的μ1、...、μm(μ1、μ2、…、μm为未知m个评价区某元素的李雅普诺夫指数)。
已知n个统计区域(模型单元):1、2、…、n,统计数据xij表示第i个统计区域(模型单元)的第j个地质变量对应的数据。
下面就某一元素来根据已知实验数据,计算它的李雅普诺夫指数,其中λi表示第i个区域中该元素的李雅普诺夫指数(λi看做已知,即可以通过前面介绍的方法计算出来)。利用多元线性回归建立如下方程组。
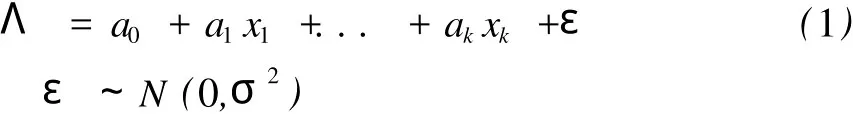
即
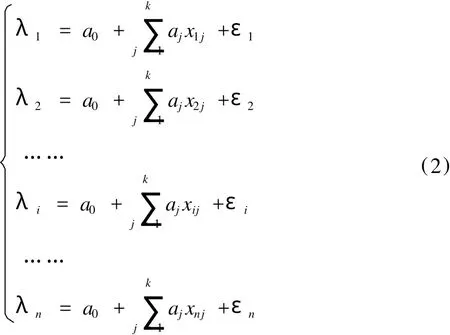
或记作
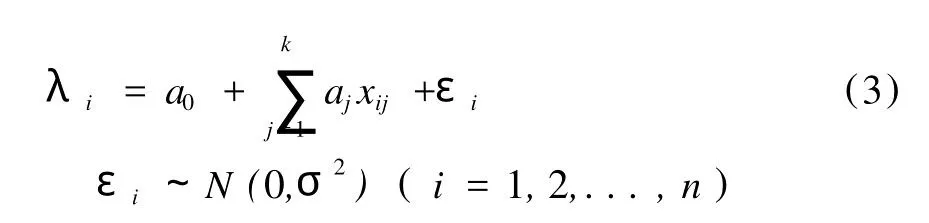
其中 a0、a1、…、ak和σ2为与xij无关的未知参数,这就是k元线性回归模型。
为了简化数学处理,引进矩阵表示,可记作
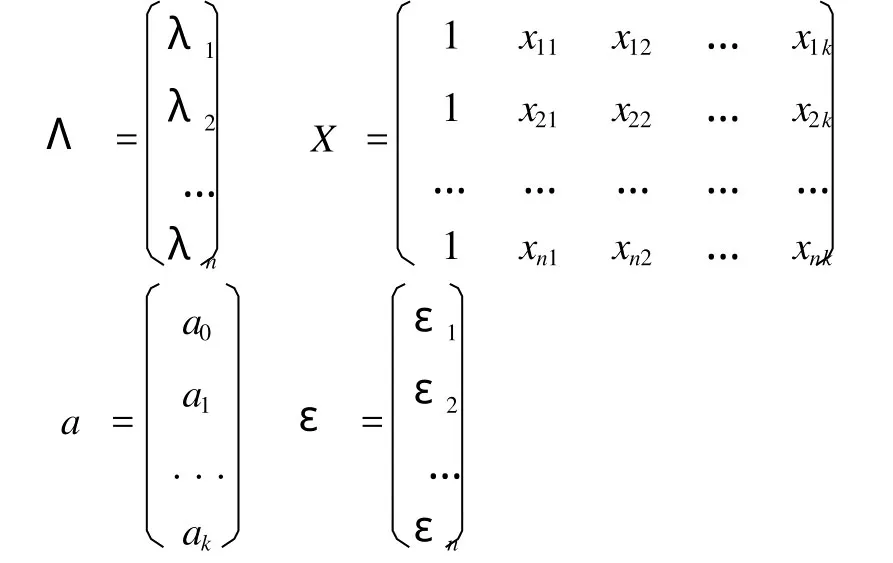
则上方程组可记作

下面用最小二乘法求未知参数的估计,即未知参数a1、a2、...、ak应使式(5)为最小。
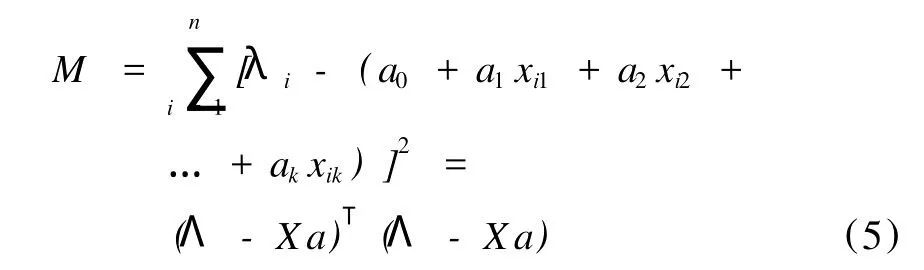
这里把M看成是与自变量aj相对应的因变量,那么问题就归结为求函数M=M(a1、a2、...、ak)在哪些点处取得最小值。由数学知识可以知道,上述问题可以通过求方程组(6)的解来解决
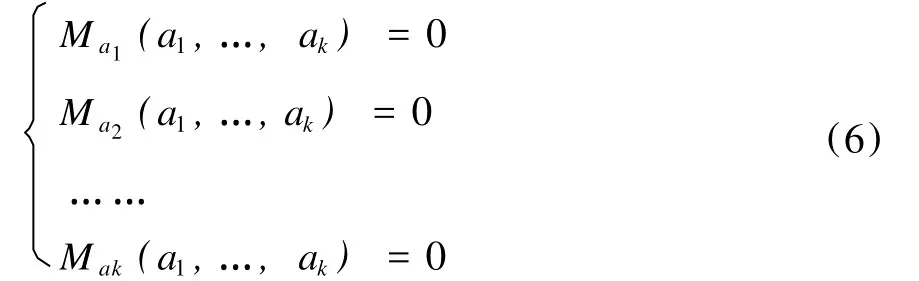
即令
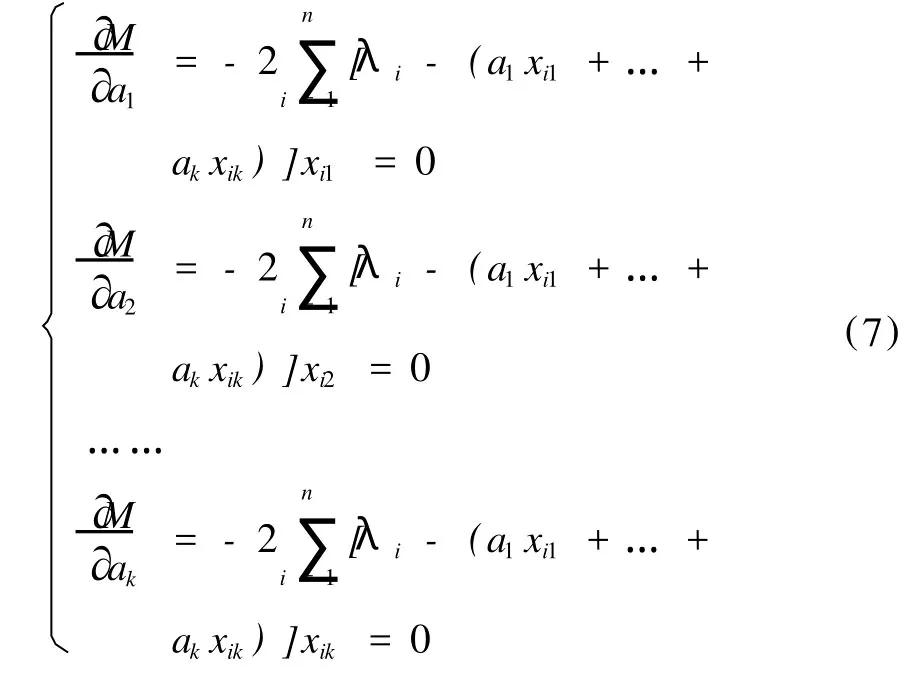
把上式整理合并,并把未知参数aj分离出来,得a0、a1、...、ak的估计:
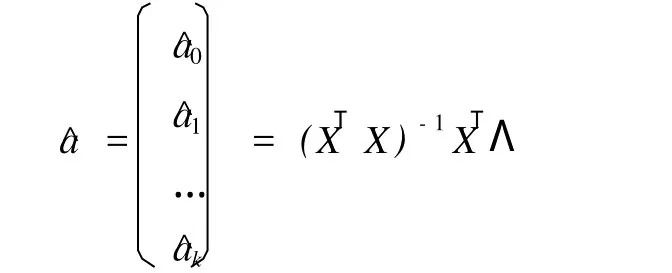
从而得到Λ与x1、x2、...、xp的经验回归方程:
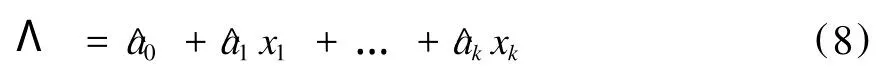
下面把a0、a1、...、ak的估计带入到μi中,则得到m个评价区中某元素的李雅普诺夫指数。
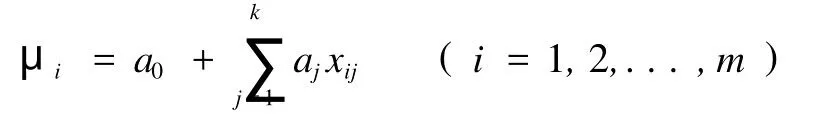
若李雅普诺夫指数大于零,则该区域成矿;若李雅普诺夫指数小于零,则可判断该区对于这种元素不成矿。
6 结论
(1)利用李雅普诺夫指数对矿产资源进行评价的方法,体现了成矿结构及演化的特征,即混沌成矿。它揭示了成矿规律与预测的一致性,并具有示性特征,反映了成矿的分类特点,是传统方法的改进(传统的方法基本上是统计的结果)。
(2)在理论上,利用李雅普诺夫指数对矿产资源进行评价,是一种资源评价的可行途径。在实际应用中,还有许多问题需要继续探讨。
[1] 单明霞.灰色系统和BP神经网络相结合的矿产资源预测模型[J].物探化探计算技术,2007,29(5):443.
[2] 赵玉琛.矿产资源预测中非参数自动化蒙特卡洛模拟程序[J].物探化探计算技术,1991,13(2):173.
[3] 赵鹏大.地质异常理论与矿床预测:现代矿产资源评价理论与方法[M].北京:地质出版社,1998.
[4] 马汉峰.矿产资源评价预测现状[J].世界核地质科学,2007,24(2):77.
[5] 王东声.混沌分形及其应用[M].合肥:中国科学技术大学出版社,2003.
[6] 李尧亭.混沌和李雅谱诺夫特征指数[J].物理,1996,25(5):282.
[7] 申维.矿化富集的耗散结构研究[J].矿物岩石地球化学通报,2000,19(4):416.
[8] 王世称,范继璋,杨永华.矿产资源评价[M].长春:吉林科学技术出版社,1990.
[9] 杨毅恒,韩燕,徐兵,等.多维地学数据处理技术与方法[M].北京:科学出版社,2002.

