含交易费用的稳健最优投资组合
程亚平,师 恪
(新疆大学数学与系统科学学院,新疆乌鲁木齐 830046)
0 引 言
在传统的Markowitz[1]均值—方差最优化模型中,其参数——资产收益的期望值和协方差矩阵都是确定的,显然这与实际不符的.F.Black等[2]指出,投资组合的选择对于均值和协方差矩阵都很敏感,尤其是均值,它的微小变化都会引起投资组合头寸的巨大改变.因此,最近研究者更多地关注于投资组合稳健性的研究.例如,D.G oldfarb等[3]研究了均值—方差模型下的稳健投资组合问题,李选举等[4]研究了带交易费用和CVaR风险测度下的稳健投资组合问题,王元英等[5]研究了不确定市场条件下的稳健最优投资组合问题,李宏杰[6]研究了带交易费用的均值—方差模型.本文主要考虑含交易费用和税收的不确定市场条件下的稳健投资组合问题.
1 模 型

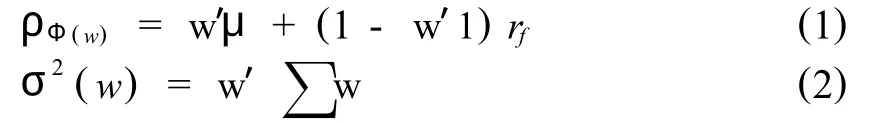
假设1 风险资产的协方差矩阵∑是确定的,且正定.

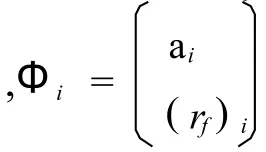
假设3 市场存在交易费用和税收,所有资产是无限可分的,且不存在卖空限制.
设每笔交易无论买入还是卖出都有α倍的交易成本,且无风险资产的利息税为β,记ai为风险资产的第i个可能期望向量,则有,ai=(a1i,…,aN
i)′.于是,含交易费用的风险资产的第 i个可能期望收益向量为,
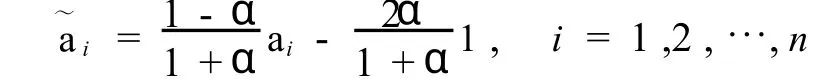

于是,由假设3有,带交易费用和税收均值收益向量Ψ不是完全确定的,而是属于某些已知向量的凸组合.记,
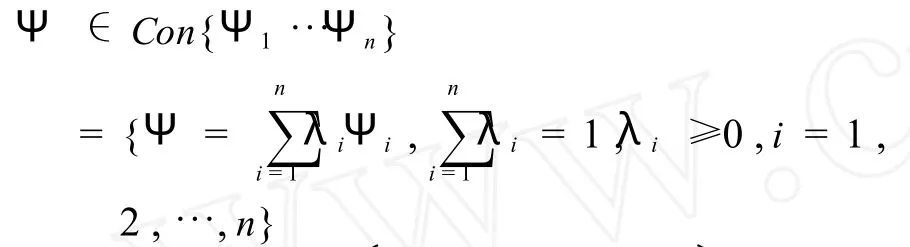
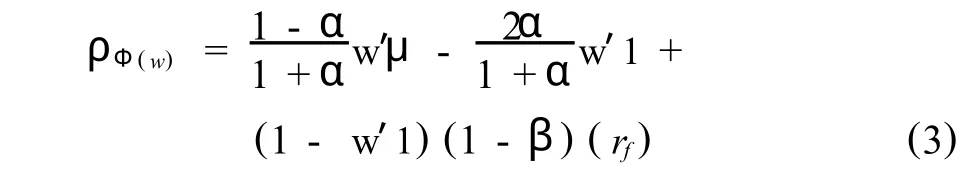
其中,μ及rf如前面所定义.特别地,由假设1,可知此时投资者总收益的方差为,

设vi表示当资产的期望收益是Ψi时投资者的期望目标向量,即满足:
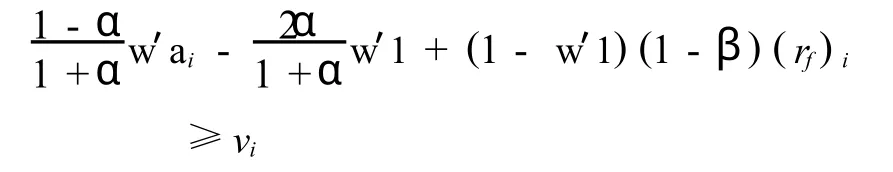
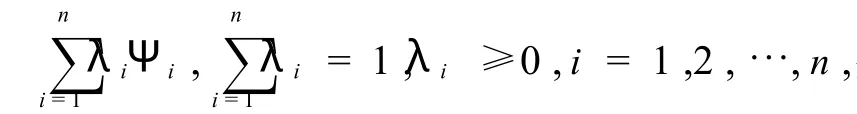
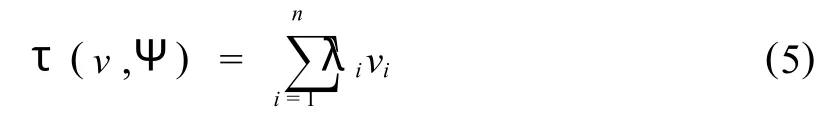
这样,期望目标值τ(v,Ψ)就由含交易费用的风险资产和含税收的无风险资产的期望收益值Ψ决定的.显然,τ(v,Ψ)=vi.
定义1 对固定的v,称投资组合w关于期望目标向量 v是稳健的,如果,pΨ(w)≥τ(v,Ψ),对任意Ψ∈Θ成立,其中,ρΨ(w)和τ(v,Ψ)分别如式(3)及式(5)定义.
定义2 对固定的期望目标向量 v∈Rn,称投资组合wv为稳健最优投资组合,如果它满足:
(i)wv关于期望目标向量v是稳健的;
(ii)对于任何关于期望目标向量v是稳健的投资组合W,都有σ2~(wv)≤σ2~(w).
定理1 以下两个命题等价.
(i)投资组合w关于期望目标向量v是稳健的.
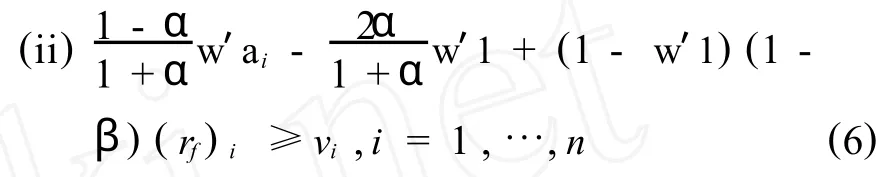
证明 (i)⇒(ii),如果 w关于期望目标向量v是稳健的,则由定义1知,
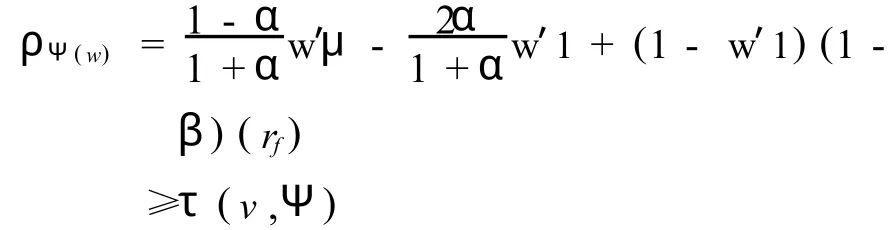
对任意的Ψ ∈Θ成立,特别地,由式(5)有,
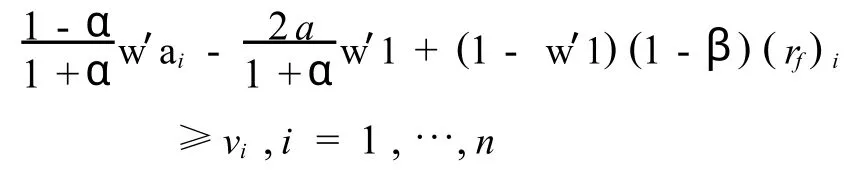

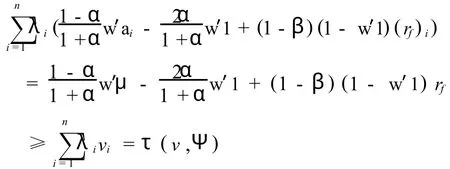
由于上式对任意的Ψ∈Θ成立,所以(i)成立.
2 模型的求解
由定理1可知,稳健最优投资组合问题等价于下述最优化问题:
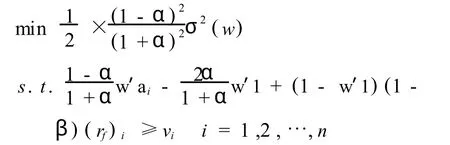
上述模型中,ai,(rf)i,vi,α,β,i=1,2,…,n,都是已知的.
模型用拉格朗日乘子法求解:
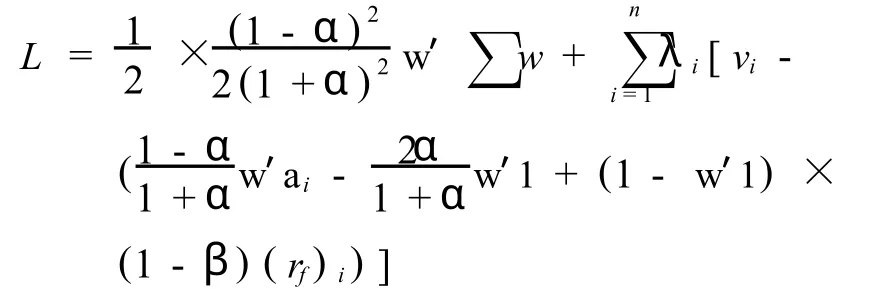
令,
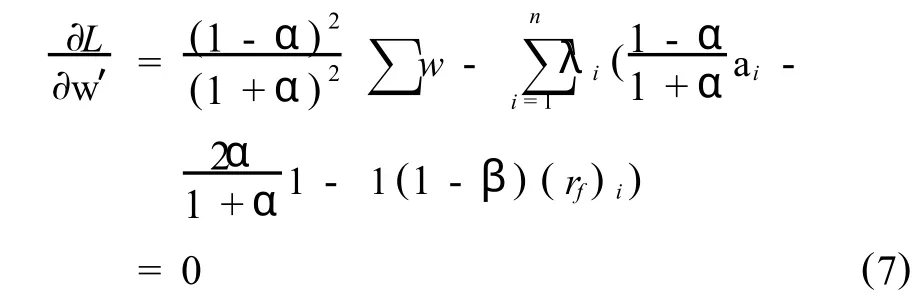
令,
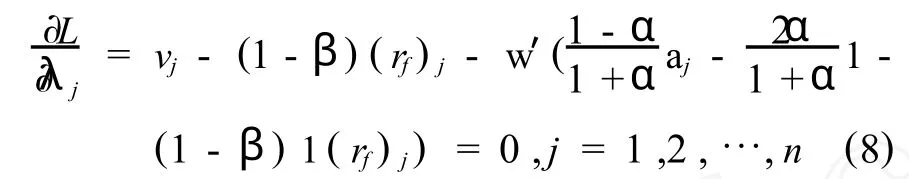

代入式(8)得,
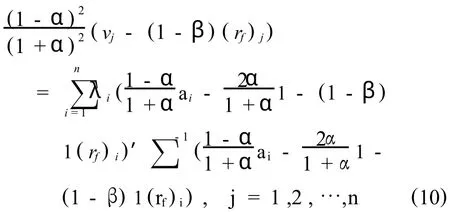
若记,

其中,η = (v1- (1 -β)(rf)1,…,vn- (1 -β)(rf)n)′,式(10)可表示为:

先讨论B满秩的情形,此时方程组有唯一解:

代入式(9)可得,

此时,稳健最优投资组合总收益的方差为:
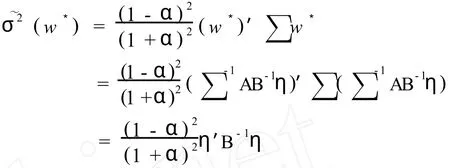
因为 B正定,故 B-1也正定,且在(v1,…,vn, σ2~)空间中是抛物面的一部分.
当矩阵B不满秩时,则矩阵A不满秩,那么含交易费用和税收的风险资产及无风险资产的超额收益向量存在相关性,于是将其中线性相关的列去掉,再按上述过程讨论即可.当假设2中的n=1时,即为带交易费用和税收,且存在无风险资产的Markowitz均值—方差最优投资组合问题.
3 结 论
本文假设风险资产和无风险资产的收益是不完全确定的,它们属于某些已知量的凸组合.同时,在市场存在交易费用和税收的情况下讨论了稳健最优投资组合问题,给出了问题的解析解,并证明了该问题等价于二次凸规划问题.
[1]Markowitz H M.Protfolio Selection[J].New Y ork:John Wiley& Sons,1952:77-91.
[2]Black F,Litterman R.Litterman,Golbal Protfolio Optimization [J].Financial Analysts Journal,1992,48(5):28-43.
[3]G oldfarb D,Iyengar G.Roburst Protfolio Selection Problems[J]. Mathematics of Operations Research,2003,28(1):1-38.
[4]李选举,高全胜.交易费用CvaR风险测度下的稳健投资组合[J].数量经济技术经济研究,2004,21(8):85-90.
[5]王元英,叶中行.不确定市场条件下的稳健投资组合[J].运筹学与控制论,2007,30(12):102-108.
[6]李宏杰.含有资本结构因子、交易费用和风险偏好的模糊最优化投资模型[J].数学的实践与认识,2008,38(11):36 -43.

