随机波浪作用下座床式大直径薄壁圆筒防波堤的动力分析空间模型
钟晓红,周锡礽,孙克俐
(1.山东交通学院土木工程系,山东 济南 250000;2.天津大学建筑工程学院,天津 300072)
随机波浪作用下座床式大直径薄壁圆筒防波堤的动力分析空间模型
钟晓红1,周锡礽2,孙克俐2
(1.山东交通学院土木工程系,山东 济南 250000;2.天津大学建筑工程学院,天津 300072)
随机波浪作用下座床式大直径薄壁圆筒防波堤的动力运动过程分为:摇摆、摇摆—小滑移运动和摇摆—大滑移运动三种运动模态,引入了控制侧向滑移的阻滑板—弹簧—阻尼器运动模型,建立了相应的动力分析空间模型。在大型有限元软件ANSYS中利用参数化设计语言APDL进行二次开发实现其空间模型,并把此空间模型计算结果与文献[1]中建立的平面模型计算结果比较,获得了一些有价值的结论,表明了本模型和方法对随机波浪荷载作用下大直径薄壁圆筒防波堤动力响应的数值模拟的可行性和有效性。
大直径薄壁圆筒;防波堤;随机波浪;动力响应;数值模拟;空间模型
引言
目前,防波堤动力分析研究主要集中在矩形沉箱防波堤在冲击荷载作用下的动力响应分析,其主要研究方法是:沿防波堤长度方向取单位长度,将其视为一个在可变形地基上运动的刚体,而地基则用弹簧或弹簧——阻尼器系统代替。因沉箱考虑为刚体且在平面内运动,这样的模型一般为三个自由度,水平位移x、竖向位移y、转动角位移φ,由此建立其动力分析平面模型,是一种简化模型。由于其三维空间圆柱壳体结构体系的特点,无论其截面形状、边界条件或作用在筒体结构上的波浪荷载沿垂直向和环向的分布均是变化的,其在随机波浪作用下的动力响应分析是空间问题。
由于空间结构复杂,而且外部荷载随时间和空间变化,不仅建立其运动方程困难,求解也相当繁杂。本文针对座床式无底大直径薄壁圆筒防波堤的受力特点,并且结合基床为散粒体而非刚性体地基的特点,提出了一种新的摇摆—滑移动力空间计算模型[1],采用竖向弹簧—阻尼模拟基床,水平向边界条件采用阻滑板—弹簧—阻尼器模拟思路,利用通用有限元软件ANSYS中参数化设计语言APDL进行二次开发建立大直径薄壁圆筒防波堤空间模型。根据运动模态的不同分别在筒底节点上布置水平铰、水平向弹簧和极限摩阻力来实现水平向各边界条件。随时间和空间变化的随机波浪荷载按分布力形式施加在薄壁圆筒的空间模型上。通过实例计算分析,本空间模型与文献[1]中的平面模型相比较,可获得更为精确的动力响应结果,并得到了一些颇有价值的结论。
1 大直径薄壁圆筒防波堤阻滑板—弹簧—阻尼器动力空间模型
结合薄壁圆筒结构沿基底滑移的滑移力P与位移x间的滑移曲线所确定的相关静摩阻力系数、极限摩阻力系数以及模拟水平边界条件的动力模式均已在文献[1]中阐述,现结合上述动力模式建立了座床式大直径薄壁圆筒防波堤的一种阻滑板—弹簧—阻尼器系统动力分析空间模型如图1所示。薄壁圆筒可能出现的运动模态仍然为:(1)水平滑移力(波浪力和惯性力)小于防波堤系统静摩阻力时的摇摆运动模态;(2)水平滑移力大于静摩阻力,且小于薄壁圆筒结构系统的综合极限摩阻力时的摇摆—小滑移运动模态;(3)水平滑移力大于薄壁圆筒结构系统的综合极限摩阻力时的摇摆—大滑移运动模态。
1.1 空间几何模型的实现
由于空间结构复杂,而且外部荷载随时间和空间变化,不仅建立其运动方程困难,求解也相当繁杂。本文利用大型有限元软件ANSYS结合薄壁圆筒结构及其自身的受力特点进行二次开发,建立了薄壁圆筒防波堤结构的一种动力响应分析空间数值模型,即采用弹性壳单元shell63模拟薄壁圆柱壳体,筒内回填料用实体单元solid45模拟。shell63和solid45之间接触处为共用耦合节点,符合力的平衡与位移协调条件。在薄壁圆筒基底与基床的接触面采用竖向线性弹簧单元combin14模拟,在筒底各节点上均匀布置竖向弹簧,弹簧另一端为固定约束,如图2所示,图中最外圈弹簧代表圆筒底趾脚下的地基。

图1 大直径薄壁圆筒防波堤的阻滑板—弹簧—阻尼器系统动力分析空间模型

图2 薄壁圆筒沿基底面的竖向弹簧布置
水平向边界条件根据上述防波堤的运动模态的不同分别采用不同方式模拟:(1)当防波堤只产生摇摆运动模态时,在筒底各节点上布置水平铰接约束。(2)当防波堤处于摇摆—小滑移运动模态时,在筒底各节点上将布置水平向弹簧,以模拟地基水平向反力。其数值将取决于静摩阻力系数fx,fx随着水平滑移量的增大而增大[1]。(3)当防波堤发生摇摆—大滑移运动模态时,在筒底节点上将直接施加基床极限摩阻力模拟地基对筒体的约束。
1.2 随机波浪荷载
1954年MacCamy和Fuchs[12]考虑附加质量效应和绕射效应,忽略流体黏滞性影响,假定波浪为有势运动,基于线性绕射理论,提出了作用在由海底延伸到水面的孤立式大直径直立墩柱上的波浪力理论计算公式,通过此公式可获得随机波浪荷载与波浪能量谱之间的传递函数。由Longuet-Higgins随机波浪模型,把波面波动可看作是一正态平稳随机过程,它可由足够多个(理论上应为无限多个)不同周期和不同随机初位相的余弦波叠加而成。采用线性叠加法,利用孤立式大直径直立墩柱上随机波浪荷载与波浪能量谱之间的传递函数及连续式大直径圆柱体的群墩影响系数,可获得作用在连续式大直径薄壁圆筒防波堤单个圆筒波峰时静水面以上和波谷时波面以下任意深度z处单位高度上的总水平波浪力P随机过程的数值模拟:
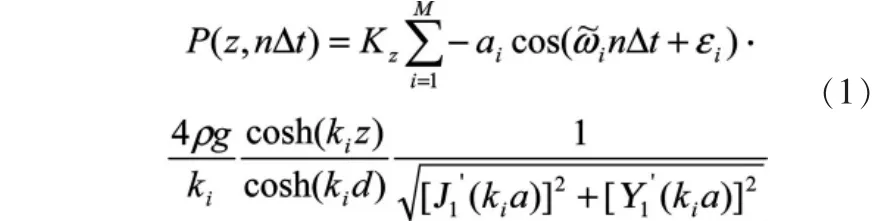
式中:d和a分别为静水面到海底深度和墩柱半径;ρ为海水密度;g 为重力加速度;ai,ki和i分别为第 i个组成波的振幅、波数和圆频率;εi为第i个组成波的初位相,是在(0,2π)上均匀分布的随机数。 Δt为时间步长;J'1(kia)和 Y'1(kia)分别是变量为kia的一阶第一类Bessel函数和第二类Bessel函数的一阶导数;Kz为连续式大直径圆柱体的群墩影响系数,可通过孤立式大直径墩柱结构上的随机波浪荷载与相同条件下的作用在连续式大直径薄壁圆筒结构上的波浪力实验值比较确定。另外,静水面到波面之间的波浪力按直线分布考虑。
由公式(1)求得的随机波浪力为单个圆筒上单位高度的总波浪力,而实际波浪力是沿圆筒周边分布的,即波压强P为:

式中:D为圆筒直径。
由以上公式获得的作用在薄壁圆筒上的随机波浪荷载不仅随时间且随空间不断变化,利用ANSYS现有窗口命令无法把荷载加载到几何模型上,本文利用ANSYS中的参数化设计语言APDL进行二次开发编写程序,把每一时间步的随机波浪荷载考虑为一工况,施加到薄壁圆筒几何模型上。
1.3 薄壁圆筒防波堤动力系统的运动方程及数值处理
根据上述空间模型,通过壳体单元与块体元以及基底的弹簧元把一个复杂的大直径薄壁圆筒结构受力体系离散为一组有限个、且按一定方式相互联结在一起的单元组合体,利用在每个单元内假设的近似函数来分片地表示整个结构上待求的未知场函数,从而使一个连续的无限自由度问题变成离散的有限自由度问题。在结构系统的动力有限元法分析中,根据假设的单元形状函数求得单元的刚度矩阵[ke]、阻尼矩阵[ce]和质量矩阵[me]等,装配得到系统的总体刚度矩阵[K]、阻尼矩阵[C]和质量矩阵[M]等,再根据滑移力(波浪力和惯性力)与结构系统地基摩阻力的比较,引入相应的地基约束条件,建立结构系统的运动方程,表示为:

式中:[M],[C]和[K]分别为结构动力系统的质量矩阵、阻尼矩阵和刚度矩阵;{u}、{u˙}和{u¨}分别为结构动力系统的位移、速度和加速度向量;[M]{u¨}称为惯性力, [C]{u˙}称为阻尼力,[K]{u}称为弹性力,{F(t)}为结构动力系统所受随时间变化的外力。
采用模态叠加法或直接积分法对上述运动方程组求解。求解后利用ANSYS中的时间-历程后处理器POST26,即可得到薄壁圆筒各个位置的位移、速度和加速度响应,以及任意时刻整个基床的应力分布。
1.4 模型中动力参数的取值
结构系统运动方程的求解,关键在于动力参数的取用,主要包括:结构动力系统质量、地基刚度系数和阻尼系数。
1.4.1 质量
结构系统有效质量、各运动模态的附加土和附加水质量可按文献[1]中方法计算取值。筒体模型分成多段建立,分别在筒上部段和下部段增加模型密度来模拟附加水质量和附加土质量,使其增加的质量和此部分质量对筒底纵向轴线的转动惯量分别与附加水和附加土对应的质量和转动惯量相等。
1.4.2 阻尼系数
在动力分析中主要考虑黏性阻尼和滞后阻尼,一般可表示成Rayleigh阻尼形式,即:

式中:α,β为系数,可定义为:

式中:ω1,ω2分别为振动体系的第一、第二阶圆频率;相应地,ξ1,ξ2分别为第一、第二阶振型的阻尼比。在计算程序中,通过规定阻尼比ξ,输入Rayleigh阻尼常数α实现黏性阻尼,输入Rayleigh阻尼常数β实现滞后阻尼。
1.4.3 弹簧刚度系数
在防波堤动力分析中弹簧刚度系数的取值对筒体位移响应影响非常明显,这一参数的确定十分重要。针对大直径薄壁圆筒结构,沿垂直向运动单位面积上的地基刚度系数k'y可采用修正后的Vessic的公式计算[7]

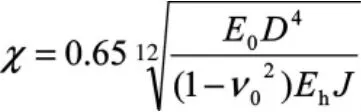
弹簧刚度系数应按其对应的平均面积下的地基垂直刚度系数取值,如图2中的弹簧1对应阴影部分面积,考虑筒底趾脚下地基刚度系数同筒内填料下的不同,其弹簧刚度系数应分别取值。
从整个空间模型动力计算分析可看出,基底竖向弹簧与水平弹簧的建立及其弹簧刚度系数的求解,以及空间圆柱表面波浪荷载的施加正是本文空间几何模型的关键点。
2 座床式大直径薄壁圆筒防波堤动力分析空间模型与平面模型算例比较分析
以山东岚山港座床式大直径薄壁圆筒防波堤为例,图3所示为其断面图,按文献[1]中方法计算出的其相关动力参数如表1所示。
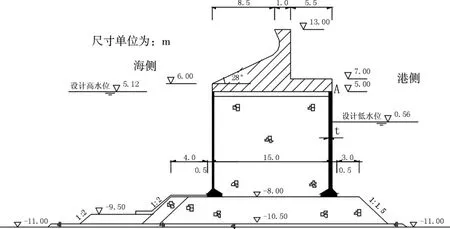
图3 山东岚山港座床式大直径薄壁圆筒防波堤断面图

表1 岚山港防波堤各项参数表
依照岚山港50 a一遇Hmax=6.8 m,Tmax=10 s的波浪要素,根据公式(2)计算出作用于圆筒上的任意高度处随机波浪压强时程,其中距筒底3 m和6 m处波压强分别如图4,图5所示。

图4 距筒底3 m处波压强时程曲线

图5 距筒底6 m处波压强时程曲线
采用如上离散元建立其空间模型,进行模态分析后,其前9阶自振频率计算结果如表2所示。从表中可看出薄壁圆筒结构最小自振频率为0.485 07 Hz,而随机波浪力属低频率荷载其频率范围主要在0.1~0.2 Hz,因此不会发生共振现象。

表2 座床式大直径薄壁圆筒结构自振频率/Hz
在文献[1]中建立的动力分析平面模型,将整个薄壁圆筒作为刚体,随机总波浪力将以合力形式作用在薄壁圆筒的中心线上。并采用四阶Runge-Kutta法求解其相应运动方程,获得结构位移响应时程曲线。
现取包含最大波浪荷载的130~180 s时间段共50 s的随机波浪荷载作用,对岚山港大直径薄壁圆筒防波堤分别采用空间模型和平面模型[1]方法计算,其各运动模态下的动力响应计算结果分别比较如下。
2.1 摇摆运动

图6 摇摆运动模态时在港侧筒顶处的总水平位移响应时程曲线
由于结构尺度较大,随机波浪荷载产生的最大滑移力远未超过静摩阻力,薄壁圆筒防波堤只发生摇摆运动,分别采用平面模型和空间模型计算的筒顶总水平位移响应时程曲线如图6所示。从图中可看出摇摆运动时平面模型与空间模型筒顶水平位移的变化趋势甚为吻合,两种模型计算出的港侧筒顶总水平位移在25.7 s时刻均达到最大,平面模型为114.84 mm,空间模型为135 mm,空间模型计算结果比平面模型大14.9%。其计算结果远小于港口工程技术规范要求。
2.2 摇摆—小滑移运动
对于薄壁圆筒直径减少为12 m,波浪要素不变,防波堤系统出现摇摆—小滑移运动模态,由平面模型和空间模型计算的筒体的水平滑移和筒顶总水平位移响应时程曲线如图7和图8所示。从图中可看出摇摆—小滑移运动时平面模型与空间模型筒顶总水平位移响应和筒体水平滑移响应的趋势很吻合。在25.6 s时刻附近平面模型和空间模型均发生小滑移运动,累计滑移量平面模型为34.8 mm,空间模型为30.3 mm,两者较为接近。港侧筒顶总水平位移平面模型为218.3 mm,空间模型为246 mm,平面模型比空间模型小11.3%。其计算结果不会影响防波堤的正常工作,符合工程规范要求。

图7 出现摇摆—小滑移运动模态时筒体水平滑移响应时程曲线

图8 出现摇摆—小滑移运动模态时筒顶总水平位移响应时程曲线
2.3 摇摆—大滑移运动
当圆筒设计直径为12 m,而波高增大为Hmax=12 m,Tmax=10 s时,防波堤系统出现了摇摆—大滑移运动模态。采用平面模型和空间模型计算的筒体水平滑移和筒顶总水平位移响应时程曲线分别如图9和图10所示。均在15 s时刻附近发生小滑移运动,累计小滑移量平面模型为36.1 mm,空间模型为33.3 mm,结果非常接近。大滑移运动均发生在25 s时刻附近,累计大滑移量分别为963.5 mm和1 000 mm,平面模型比空间模型小5%。港侧筒顶最大总水平位移分别为1 370.1 mm和1 458.6 mm,平面模型比空间模型小8%。由于水平滑移和筒前趾沉降过大,使防波堤破坏,并且极易导致防波堤基床的整体破坏模式[12]。由此可看出,一旦防波堤出现摇摆—大滑移运动模态,则防波堤系统将遭受完全破坏。

图9 出现摇摆—大滑移运动模态时筒体水平滑移响应时程曲线

图10 出现摇摆—大滑移运动模态时筒顶总水平位移响应时程曲线
从以上比较结果可看出,无论那种运动模态按平面模型计算出的筒顶处的总水平位移均比空间模型计算结果小,但差值最多不超过15%。其主要原因是平面模型把圆筒简化为一绝对刚体,整体性显然比空间模型好。而空间模型考虑了薄壁圆筒和筒内填料的实际弹性模量,并且将结构离散成多个自由度的计算问题,这更接近于工程实际情况。若在空间模型中把筒内填料弹性模量取为与筒壳结构相同的弹性模量,将薄壁圆筒视为一刚性圆筒体。此时,按空间模型计算摇摆运动模态时的水平位移响应时程如图11所示,在25.7 s时刻附近筒顶处的最大水平位移为118.3 mm,与平面模型筒顶最大水平位移114.84 mm较为接近,只相差约3%。

图11 刚性圆筒空间模型港侧筒顶总水平位移响应时程曲线图

图12 空间模型摇摆运动产生的筒底部分基床应力分布
其次,空间模型沿筒底均布置竖向弹簧,且依据公式(6)趾脚下的基床竖向弹簧系数比筒内填料下的小,而平面模型中筒体与基床土体间的接触采用一个转角弹簧—阻尼系统替代,此弹簧系数为趾脚下和筒内填料下的基床刚度系数按相应的面积加权平均确定的一种简化取值,这也使得平面模型的位移计算具有一定误差。
在不考虑筒体自重情况下,薄壁圆筒在摇摆运动模态时的空间模型动力响应计算中,在25.7 s时刻的部分筒底基床应力分布如图12所示。从图中可看出,此时薄壁圆筒位于90°纵轴处的基底应力出现较小的负值,表明此处基床受压。这说明圆筒在随机波浪作用下产生摇摆运动时其转动中心未必正在90°纵轴处(略微往圆筒后趾偏移)。实际上,随着波浪荷载的变化,防波堤系统摇摆中心将出现在结构底纵轴附近一定的范围内。而平面模型限定圆筒摇摆转动中心为90°纵轴处,这也是造成平面模型与空间模型计算结果不同的又一原因。
3 结论
(1)本文根据试验结果,把在随机波浪作用下的座床式大直径薄壁圆筒防波堤的运动分为三种运动模态:摇摆、摇摆—小滑移、摇摆—大滑移运动模态。同时引入了侧向阻滑板—弹簧—阻尼器的模型体系,根据不同的运动模态分别在筒底节点上加水平铰、水平向线性弹簧和极限摩阻力模拟地基水平边界条件,建立了动力分析空间模型。在大型有限元软件ANSYS中利用参数化设计语言APDL进行二次开发实现其空间模型的动力响应分析。
(2)从以上分析比较可看出平面模型和空间模型的计算结果其变化趋势是相符的,但数值略有不同,在本算例中二者相差未超过15%。空间模型显然更符合薄壁圆筒防波堤的实际受力情况,但建模施加荷载计算繁杂。平面模型简单易算,因此对平面模型计算结果乘以1.15~1.2的修正系数,其结果也可以在初步设计中使用。
(3)从用平面模型和空间模型对实际工程的计算与验证表明,结构底与基床为散粒体材料接触的防波堤发生微小滑移时,防波堤可以正常工作,因此座床式大直径薄壁圆筒防波堤设计时应允许其可能发生的小滑移,一旦防波堤出现摇摆—大滑移运动模态,则防波堤系统将遭受完全破坏。平面模型与空间模型均可对随机波浪作用下大直径薄壁圆筒防波堤的动力响应进行数值模拟,能给出防波堤相关的水平位移、竖向位移、转角及相应的速度、加速度时程响应和滑移力的时程响应及任意时刻地基应力分布,并能很好地反映大直径薄壁圆筒防波堤系统的动力运动全过程。
[1]钟晓红,周锡礽,等.随机波浪作用大直径薄壁圆筒防波堤的动力分析模型[J].水利学报,2006(4):464-470.
[2]钟晓红,周锡礽,等.随机波浪作用下圆沉箱防波堤的动力分析模型[J].中国科学E辑技术科学,2007(11):1480-1490.
[3]Goda Y.Dynamic response of upright breakwaters to impulsive breaking wave forces[J].Coastal Engineering,22:135-158.
[4]Oumeraci H,Kortenhaus A.Analysis of the dynamic response of caisson breakwaters[J].Coastal Engineering,1994,22:159-183.
[5]中交第三航务工程勘察设计院.码头新型结构[M].北京:人民交通出版社,1999.
[6]M G哈勒姆,N J黑弗,L R伍顿.海洋建筑物动力学[M].北京:海洋出版社,1981.
[7]C H列瓦切夫.薄壳在水工建筑物中应用[M].北京:人民交通出版社,1982.
[8]周锡礽,潘厚志.基床系数法在深埋式大圆柱壳结构数值模拟中的应用与改进[J].水利学报,2001(5):62-66.
[9]钟晓红,周锡礽,钱荣,基床式大直径薄壁圆筒结构内力计算的弹簧元数值模型[J].港工技术,2005(1):22-25.
[10]钱荣.大直径圆柱壳结构动力响应及随机波浪力数值模拟研究[D].天津:天津大学博士论文,2004.
[11]岚山港大直径薄壁圆筒防波堤断面模型试验报告[R].天津大学,1994.
[12]J D Srensen,H F Burcharth.Reliability analysis of geotechnical failure mode for vertical wall breakwaters[J].Computers and Geotechnics,2000,26:225-245.
[13]竺艳蓉.海岸工程波浪力学[M].天津:天津大学出版社,1991:100-112.
The Space Model of Dynamic Analysis of Seated Large Diameter Cylinder Breakwater under Random Waves
ZHOU Xiao-hong1,ZHOU Xi-ren2,SUN Ke-li2
(1.Department of Civil Engineering,Shandong communications college,Jinan Shandong 250000,China;2.School of Civil Engineering,Tianjin University,Tianjin 300072,China)
According to the three motion modes of motion process of the seated large diameter cylinder breakwater (LDCB)under random waves,the dynamic model system composed of antislider-spring-damper to control the lateral sliding is introduced.The corresponding dynamic analysis space model is established.The space model is realized by Parameter Design Language APDL in the large finite element software ANSYS.The calculated result by the space model is compared to those by plane model respectively and some valuable conclusions are achieved.The validity of the model which can be used in dynamic response analysis of the seated LDCB under random waves is confirmed by the given example.
the large diameter cylinder;breakwater;random waves;dynamic response;numerical simulation;space model
P75
A
1003-2029(2010)04-0102-07
2010-07-10
国家自然科学基金资助项目(59909005)
钟晓红(1978-),女,四川隆昌人,硕士,讲师,从事港口、海岸及近海工程研究。E-mail:zhongxh1123@sina.com

