基于多波束数据的声速误差自动改正方法

胡 佳 ，李明叁 ，孙 强

(1.海军大连舰艇学院 研究生管理大队，辽宁 大连 116018；2.海洋测绘科学与工程系，辽宁 大连 116018)

基于多波束数据的声速误差自动改正方法

胡 佳1，李明叁2，孙 强1

(1.海军大连舰艇学院 研究生管理大队，辽宁 大连 116018；2.海洋测绘科学与工程系，辽宁 大连 116018)

讨论了声速误差对多波束测深值的影响，在此基础上，建立了自动搜索等效声速剖面的改正方法。该方法利用多波束实测数据搜索等效声速剖面，取代实测声速剖面，可削弱声速误差的影响。实例计算表明，利用多波束实测数据建立的声速剖面自动改正方法，能够有效地消除声速误差的影响，并且在处理过程中不需要人工干预，较大地提高了改正效率。

声速误差；多波束测深；声速剖面

引言

声速改正是多波束测深中最为重要的误差改正之一，如何提高改正精度一直是海洋测量者研究的热点。一般而言，完整的声速改正应当包括两个方面：一是声线折射改正，即声波在不同声速的水层传播时会发生折射，改变了波束脚印的位置，需要根据声速数据构建声线跟踪模型，校正深度和水平距离。二是声速误差改正，由于仪器精度限制以及声速剖面代表性误差[1]影响等，获得的声速剖面并不是测点真实声速剖面，而是存在一定误差，称为声速误差，会对测深产生直接影响，需要进行改正。对于声线折射改正，相关的理论与技术较为成熟，提出了精细的改正模型[2]，可以获得较高精度；而对于声速误差改正，由于测点实际声速剖面难以获得，目前常采用后处理方式改正，例如商用软件CARIS HIPS中就集成了相关后处理模块，但是这种后处理过程通常需要人工干预，即需要由测量者不断调整改正量并根据数据表现出的地形特征自主确定改正是否完成，效率较低并且改正的质量难于量化，在这种情况下，研究声速误差改正的自动化是很有必要的。为此，本文以实测多波束数据为基础并结合等效声速剖面法[3]，尝试建立一种声速误差的自动改正方法。

1 声速误差的自动改正方法

在实际测量中，测点真实声速剖面的未知性极大增加了声速误差改正的难度。但是根据Geng和Zielinski的理论[4]：具有相同传播时间、表层声速和相同声速剖面积分面积的声速剖面族，波束位置的计算结果相同，任何复杂的声速剖面均可用一个常梯度声速剖面等效，如果能够获得测点的等效声速剖面，就可绕开求取真实声速剖面的难点，直接由等效声速剖面法改正声速误差。等效声速剖面可根据多波束数据表现出的地形特征来确定，每设计一个声速剖面可获得一种改正后的海底地形，当为等效声速剖面时，用其改正后的海底地形一定最接近真实际情况，这就为自动搜索等效声速剖面提供了可能，声速误差改正的自动化也正是在这种自动搜索中被体现的。鉴于在搜索过程中需要利用给定的声速剖面改正测深值，本文在介绍等效声速剖面的自动搜索法之前，给出了相应的算法。

1.1 利用等效声速剖面改正测深值

等效声速剖面模型如图1所示，合理地调整表层声速C0和声速梯度g，声速剖面积分面积S随之改变，实现复杂声速剖面的替换[5-6]。

图1 等效声速剖面示意图

于是，等效声速剖面可由参数c0与g表示，则深度h为[3]：

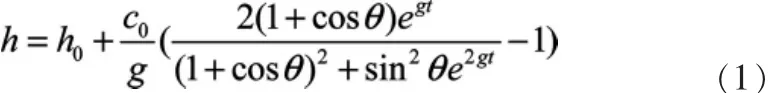
式中：h0为换能器吃水；θ为波束角；t为波束单程传播时间。对于某“Ping”，对应的海底地形是已知的，通过含有误差的声速剖面获得。假设该声速剖面仅有一个声速层，声速为1 500 m/s，如果获得了参数c0与g，则可根据不同的横距采样值 yi和深度 hi反求 θi和 ti，再由（1）式计算改正后的 hi。 这里假设的声速剖面仅仅是为了反求参数的需要，无须考虑含有误差的量级，所以设为常声速是合理的。

1.2 等效声速剖面的自动搜索确定

确定等效声速剖面事实上是确定参数c0与g，可采用Fibonacci算法[7]自动搜索，c0的范围取[1 450 m/s,1 550 m/s]，g的范围取[-1.732°,1.732°]，相当于图 3 中角 α 在[-60°,60°]间变化，该范围基本上可以涵盖任何实际声速剖面的积分面积。

搜索终止的判定准则由条带数据表现出的地形特征来确定。一般认为声速误差对中央波束影响小，当水深不大时，单“Ping”的深度可近似采用中央波束的深度值表示，考虑到可能存在坡度，相邻条带相交“Ping”的海底地形可近似由两个中央波束深度值的连线表示，形成如图2所示的相交“Ping”模型。

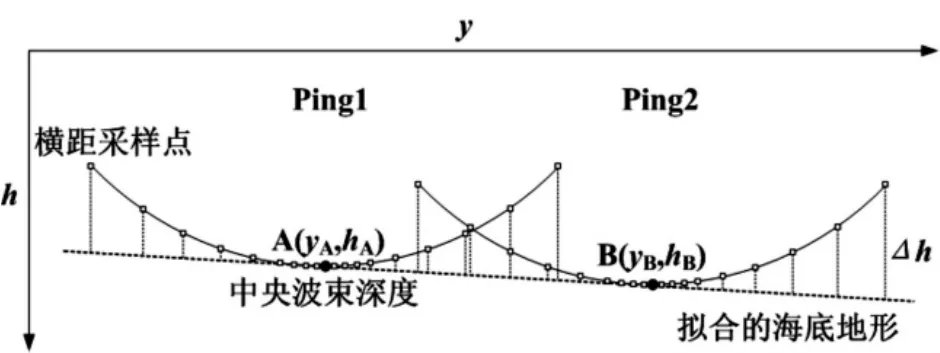
图2 相邻条带相交“Ping”示意图

图2 中两条曲线表示受声速误差影响的实测海底地形，直线表示由两个深度平均值构建的海底地形，两种地形的差异可由式（2）量化：

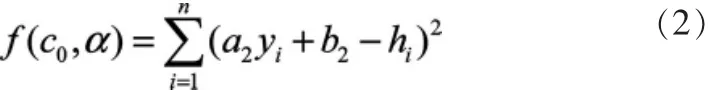
式中：n为横距采样数；a2，b2为直线方程的参数；yi为采样点i的横距；hi为在采样点i处由参数c0与g利用（1）式改正后的深度。不同的c0与g可以获得不同的hi，使函数f（c0,α）的值发生变化。显然，如果搜索到恰当的c0与g，两种海底地形应最为接近，即f（c0,α）获得最小值，此时终止搜索，获得的海底地形即为声速误差改正后的海底地形。

1.3 声速误差的改正算法

结合自动搜索等效声速剖面的相关理论并顾及测量的实际情况，本文提出了下述声速误差的自动改正算法：

（1）测区分块：将测区分成若干个矩形子区域，每个子区域的长度恰好覆盖两个条带，宽度可依据水深区间确定，以避免地形起伏的影响。

（2）建立相交“Ping”模型：每个子区域均包含两个条带，分别求取其中央波束的平均深度，用二者的连线构建海底地形；然后在中央波束两侧分别选取数目相等的若干采样点，求其平均深度并拟合成曲线，表示受声速误差影响的实测海底地形，完成相交“Ping”模型的建立。

（3）确定等效声速剖面：基于相交“Ping”模型，利用 Fibonacci自动搜索算法确定等效声速剖面的表征参数c0与g。

（4）声速测量误差的改正：获得等效声速剖面后，对子区域中条带的每一“Ping”用（1）式计算测深值，完成声速误差的改正。

2 声速误差对测深值影响的讨论

由于在搜索等效声速剖面时作了声速误差对中央波束影响小的假设，是本文方法的理论基础，其成立与否需要得到证明，具体的影响量级也需要量化；另外，测量时可能有其他参数会改变声速误差对测深的影响规律，使用于搜索等效声速剖面的相交“Ping”模型发生变化，降低搜索结果的可靠性，所以，在应用本文方法之前，讨论声速误差对测深值的影响是很有必要的。

在多波束测深中，声速误差对测深值的影响主要包括三部分：

（1）直接影响：声速、声波传播时间以及深度之间具有物理上的相互联系，声速误差通过这种联系直接对深度值产生影响；

（2）表层声速误差的影响：除了直接影响外，当多波束系统具有波束束控时，表层声速误差还通过影响波束角间接对深度值产生影响[8]。

（3）声速剖面扩展的影响：若声速剖面的测量深度小于实际深度，多余部分将没有适当的声速数据辅助计算，会对深度值产生影响。

忽略声线弯曲，上述三部分的影响可表示为[9]：

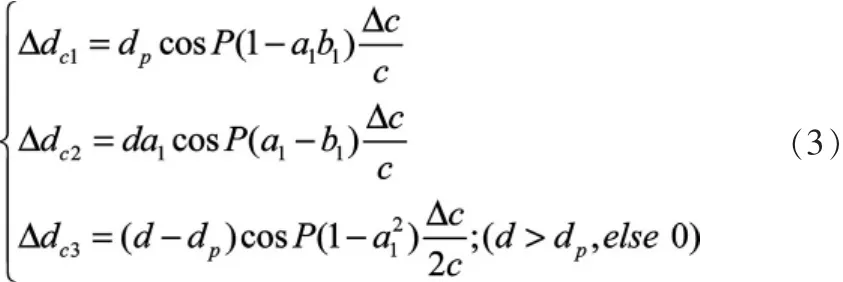
式中：Δdc1表示直接影响造成的深度误差；Δdc2表示表层声速误差的影响造成的深度误差；Δdc3表示声速剖面扩展的影响造成的深度误差；a1=tan（θ+R）；b1=tan（θ-β-R）； θ为波束角；R，P分别为测船横、纵摇；β为换能器安装偏角；d为中央波束测量深度；dp为声速剖面测量深度；c为实际声速；Δc为声速误差。若多波束系统无波束束控，则（3）式中含有b1的多项式不存在。综合这三部分影响，可将深度误差近似为：

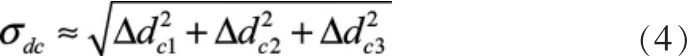
事实上，一般情况下纵摇小于5°，而θ和R是决定声速测量误差影响规律的主要参数，这是因为一旦换能器安装好后，β是一个常数，且在波束一次发射后，获得的d和dp值也是确定的。在仅顾及θ及R的影响时，声速误差对有无束控的影响规律是相似的，故这里仅列出无波束束控时的深度误差：

根据（5）式，仅顾及波束角变化时，令声速为1 500 m/s，声速误差为1.0%，横摇为0°，实际深度为100 m，声速剖面测量深度为80 m，计算波束角在-75°～75°之间变化时深度误差的大小，结果见图3；仅顾及横摇变化时，将波束角选取为具有代表意义的若干数值，除横摇外其余参数取值不变，计算横摇在-5°～5°间变化时深度误差的大小，结果见图4。

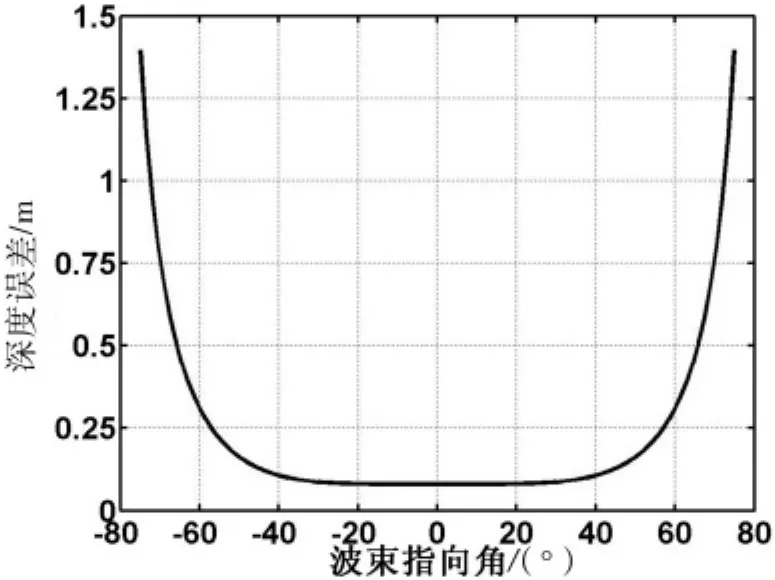
图3 不同波束角下声速误差对测深值的影响

图4不同横摇下声速误差对测深值的影响

图3 表明，声速误差对中央波束的测深值影响量级较小，约0.08 m，对边缘波束，尤其是大于50°的波束的影响非常大，在边缘波束处，深度误差超出IHO规定的1%水深限差。

图 4 的曲线分别表示了波束角为 0°，45°，60°，67.5°，72.5°和±75°时深度误差与横摇之间的变化关系，结果表明：

（1）横摇对中央波束附近测深值的影响很小，横摇为5°比为0°时深度误差几乎不变，均约为0.08 m，45°波束角处的深度误差较0°也仅增加了约0.08 m。

（2）横摇对边缘波束的影响较大，75°波束角的深度误差从横摇为0°时的1.40 m增大为5°时的3.23 m，增幅约2.3倍，-75°波束角也有类似的结论。

（3）横摇使深度误差超限的临界波束角减小，从横摇为0°时的 72.5°减小到为 5°时的 67.5°。

总体来看，声速误差对中央波束的影响确实较小，对边缘波束的影响则较大，所以用中央波束的测深值作为声速改正误差的参考值是合理的。

3 实例验证

为了验证本文方法的有效性，以某海区2008年勘测的多波束数据进行分析，采用的是Seabat8111多波束系统。算例选取了其中的6条主测线和1条检查测线，主测线间隔约290 m，宽度约490 m，长约5.9 km，水深变化范围为49.2～63.1 m；检查线主要用于检验改正效果，并不参与改正。剔除异常数据并加入各项改正（姿态、潮汐及时间延迟等）后，将各测线数据用图像的方式表示如图5。

由于用于计算的声速剖面存在误差，图5中主测线的水深值呈现中央波束大，边缘波束小的特点，使得整个图像出现明显的分层，这种层状海底地形是不真实的，需要进行改正。根据声速误差改正算法，本文形成了如下的改正步骤：

图5 含有声速测量误差的多波束条带数据

（1）将整个测区分成若干个矩形子区域，这里将矩形的宽度统一取为300 m，包含数据约150“Ping”（图5中白色矩形），该区域中央波束沿航向的深度变化小于1.0 m，不会因地形起伏给等效声速剖面的搜索带来较大影响。

（2）在每个子区域中分别建立相交“Ping”模型，搜索等效声速剖面。用于构建实测海底地形采样点个数为中央波束两侧按等距各取50个，共计101个采样点，对应Seabat8111系统的101个波束。

（3）利用获得的等效声速剖面改正测深值。

下面基于图5中白色方框区域，详细阐述声速误差的改正过程，该范围的数据见图6（a）。为了便于观察，适当扩大了图中横距比例，可以看到，图中数据呈现明显的“笑脸”状弯曲。

由步骤（2）得到图 6（a）所示曲线，完成相交“Ping”模型的构建。基于此模型自动搜索区域内等效声速剖面，获得参数Co值为1 500 m/s，g值为-0.325。利用这一结果对图6（a）所示数据进行声速误差改正，结果见图6（b）。

从图6（a）、（b）的比较可以看出，经过声速误差改正后，数据分布均匀、平坦，集中在56.2 m水深值附近，原先的“笑脸”状弯曲基本消失，获得了很好的改正效果。

对所有的矩形区域均采用上述步骤进行处理，得到了图7所示图像，与图5比较后可看出，经过处理后的海底地形不再出现层状失真，条带间拼接完好，较为真实地反映了海底的地形概况。经检查线中央波束的测深值比对后，最大相差约0.37 m，最小相差约0.12 m，满足IHO精度要求，说明了本文方法的有效性。

图6 声速测量误差的改正过程

4 结论与建议

（1）声速误差对中央及附近波束的测深值影响较小，对边缘波束的影响较大。

图7 声速测量误差改正后的多波束条带数据

（2）测船横摇会较大的改变声速误差地影响规律，使某一边缘波束的深度误差显著增大，减小了深度误差超限的临界波束角。因此，建议在进行声速测量误差改正前，首先进行横摇校正。

（3）基于多波束数据的声速误差自动改正方法，较好的消除了声速测量误差对多波束测深的影响，并且在处理过程中不需要人工干预，有利于提高多波束数据处理效率。

应当指出的是，虽然量级很小，但声速误差对中央波束也有影响。本文方法以中央波束的深度作为参考值，改正后会留有部分残差，可通过提高实测声速剖面的精度来消除，这也说明了本文方法的改正精度对实测声速剖面的精度具有一定的依赖性。尽管如此，该方法对边缘波束的改正效果还是十分明显的。

[1]丁继盛,张卫红.声速断面对多波束测深的影响[J].海洋测绘,1998,(3):15-19.

[2]赵建虎.多波束深度及图像数据处理方法研究[D].武汉:武汉大学测绘学院,2002.

[3]赵建虎,刘经南.多波束测深及图像数据处理[M].武汉:武汉大学出版社,2008:130-132.

[4]Xueyi Geng,Adam Zielinski.Precise Multibeam Acoustic Bathymetry[J].Marine Geodesy,1999,(22):157-167.

[5]阳凡林,李家彪,吴自银，等.浅水多波束勘测数据精细处理方法[J].测绘学报,2008,37(4):444-450.

[6]Kammerer E.New Method for the Removal of Refraction Artifacts in Multibeam Echosounder Systems[D].The University of New Brunswick,2000.

[7]Cheney W,D Kincaid.Numerical Mathematics and Computing[M].Brooks/Coles Publishing Company,1980.

[8]Dinn D F,Loncarevic B D,G Costello.The effect of sound velocity errors on multi-beam sonar depth accuracy[C]//Proceedings of Oceans’95,1995：1001-1010.

[9]Rob Hare.Error Budget Analysis for US Naval Oceanographic Office (NAVOCEANO)Hydrographic Survey Systems[S].Final Report for Task 2,FY 01,September 2001.

The Automatic Correction for Sound Speed Error Based on Multibeam Sounding Data

HU Jia1,LI Ming-san2,SUN Qiang1
（1.Dept.of Graduate Management,Dalian Naval Academy,Dalian Liaoning 116018,China;2.Dept.of Hydrography and Cartography,Dalian Naval Academy,Dalian Liaoning 116018,China）

The effect of sound speed error upon multibeam sounding data was discussed.Based on the result,an automatic correcting method had been proposed,which firstly searched the equivalent sound velocity profile (SVP)through multibeam sounding data,then utilized it to correct sound speed error instead of the real SVP.An example was given to prove that the automatic correcting method was effective and efficient.

sound speed error;multibeam sounding;sound velocity profile

TB566

A

1003-2029（2010）04-0066-05

2010-06-03

国家自然科学基金资助项目（40871207）

胡佳(1985-)，男，湖南湘潭人，硕士研究生，主要从事海洋测深数据处理研究。