三维模拟高温高静水压下矿物颗粒边界应力分布

陈玉香 ，杜建国，刘红，张建平

(1. 中国地震局 地质研究所，北京，100029；2. 中国地震局 地震预测研究所，北京，100036；3. 湘潭大学 机械工程学院，湖南 湘潭，411105)

探明岩石、矿物的力学性质与变形机制，有助于了解地球内部动力学过程[1]。岩石、矿物的力学性质与变形机制取决于矿物成分、结构、矿物颗粒边界效应和温压条件等多种因素。Holtzman等[2−4]沿用非静水压下岩石、矿物的应变率与差应力具有幂律关系的流变经验公式，并考虑颗粒粒径[5]、氧逸度[6]、流体[7−8]、活化体积[9]及其综合因素[10]的影响模拟研究岩石、矿物的变形机制。随着计算机技术的迅速发展，越来越多的研究者用数值模拟方法宏观模拟研究岩石的力学性质尤其是对岩石裂纹体的断裂机制[11]，并应用于岩土工程中。近年来，杨振涛等[12−13]采用数值模拟单矿物与双矿物岩石在差应力下的流变性质。然而，人们还只是借助于数值模拟方法探讨矿物集合体中颗粒边界移动的结果[14]、边界湿化对矿物颗粒集合体剪应力分布的影响[15]。事实上，矿物颗粒边界是具有大离子半径的元素的重要集聚地[16]，在一定的温度、压力条件下，矿物颗粒边界能形成反应边构造，生成新的矿物[17]或使颗粒边界湿化[18]，从而影响岩石的变形机制以及弹性波速、电导率等[19]。矿物颗粒边界效应作为影响岩石、矿物力学性质与变形机制的重要因素之一，人们对其研究较少。为此，本文作者应用ANSYS有限元软件三维模拟计算在高温800 ℃、高静水压1.6 GPa条件下，上地幔、下地壳重要组成矿物镁橄榄石与透辉石集合体在加压瞬间完全弹性变形阶段颗粒边界层的应力场，进而分析探讨静水压下2种不同矿物颗粒边界层的应力分布规律。

1 研究方法

1.1 计算模型

参照桑祖南等[20]对单斜辉石颗粒尺寸(长轴长度平均为0.224 mm，短轴长度平均为0.096 mm)的描述。镁橄榄石、透辉石颗粒采用立方体结构，立方体边长为 0.2 mm；颗粒边界为 2种矿物的过渡层，厚度为5 µm。

由于矿物颗粒为立方体结构，不能将其简化为平面应变或带厚度的平面应力问题，从而直接建立三维模型。矿物颗粒排列从下至上依次为镁橄榄石颗粒、透辉石颗粒、镁橄榄石颗粒。根据对称性，建立笛卡儿坐标系，对称中心为坐标原点O，取整体模型的1/8(称为计算模型)进行计算。图1所示为计算模型几何图，上层为镁橄榄石，下层为透辉石，中间薄层为颗粒边界。采用ANSYS内置的Solid65单元类型、规则网格(在X轴和Z轴方向划分20等分，在Y轴上的透辉石层划分20等分，颗粒边界层划分20等分，镁橄榄石层划分40等分)，计算模型中共有32 000个规则单元、35 721个节点和107 163个自由度。

图1 计算模型几何图Fig.1 Geometric plot of computed model

模型中矿物颗粒层、矿物颗粒边界层都为各向同性弹性材料；矿物颗粒与颗粒边界层之间接触良好，既不考虑空隙，也不考虑两矿物颗粒之间的摩擦。对称中心O点固定，XOZ面上Y向位移为0，XOY面上Z向位移为0，YOZ面上X向位移为0；各外表面加载1.6 GPa均布压力即静水压力。

1.2 计算参数

在计算过程中所需要的弹性模量E、泊松比ν计算式如下：

其中：Ks为体积模量；G为剪切模量。

在温度为800 ℃、压力为1.6 GPa 条件下，镁橄榄石的体积模量与剪切模量从 Anderson等[21]得出的高温下地幔矿物的弹性常量表中直接查得；而透辉石的体积模量与剪切模量从 Bass[22]整理的立方晶体矿物的弹性模量表中查到，在室温、常压下，它们分别为114 GPa和64.9 GPa。计算模型中透辉石、镁橄榄石的弹性参数见表1。

颗粒边界层为透辉石与镁橄榄石这2种矿物的过渡层，其组成物质的体积模量Ks3、剪切模量G3计算式为：

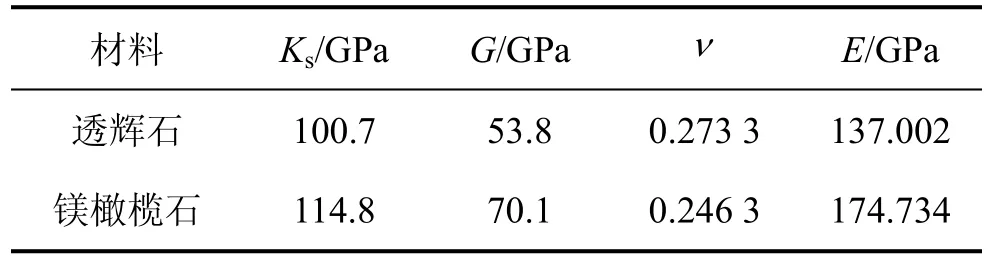
表1 在800 ℃和1.6 GPa条件下透辉石和镁橄榄石的弹性参数Table 1 Elastic parameters of diopside and forsterite at 800 ℃ and 1.6 GPa

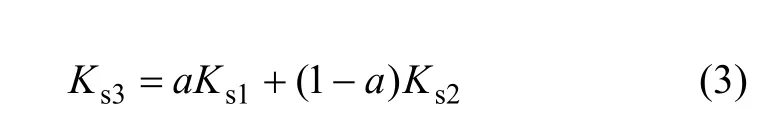
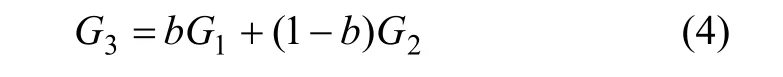
其中：Ks1为透辉石体积模量；Ks2为镁橄榄石体积模量；G1为透辉石剪切模量；G2为镁橄榄石剪切模量；a为颗粒边界层组分矿物透辉石的体积模量系数；b为颗粒边界层组分矿物透辉石的剪切模量系数。

由于本文是计算静水压为1.6 GPa时颗粒边界层的应力，重点考虑体积模量的影响，故选取b为固定值0.5，a从0至1之间变化，根据式(1)～(4)计算得到相应的颗粒边界层的弹性模量E与泊松比ν，见表2。

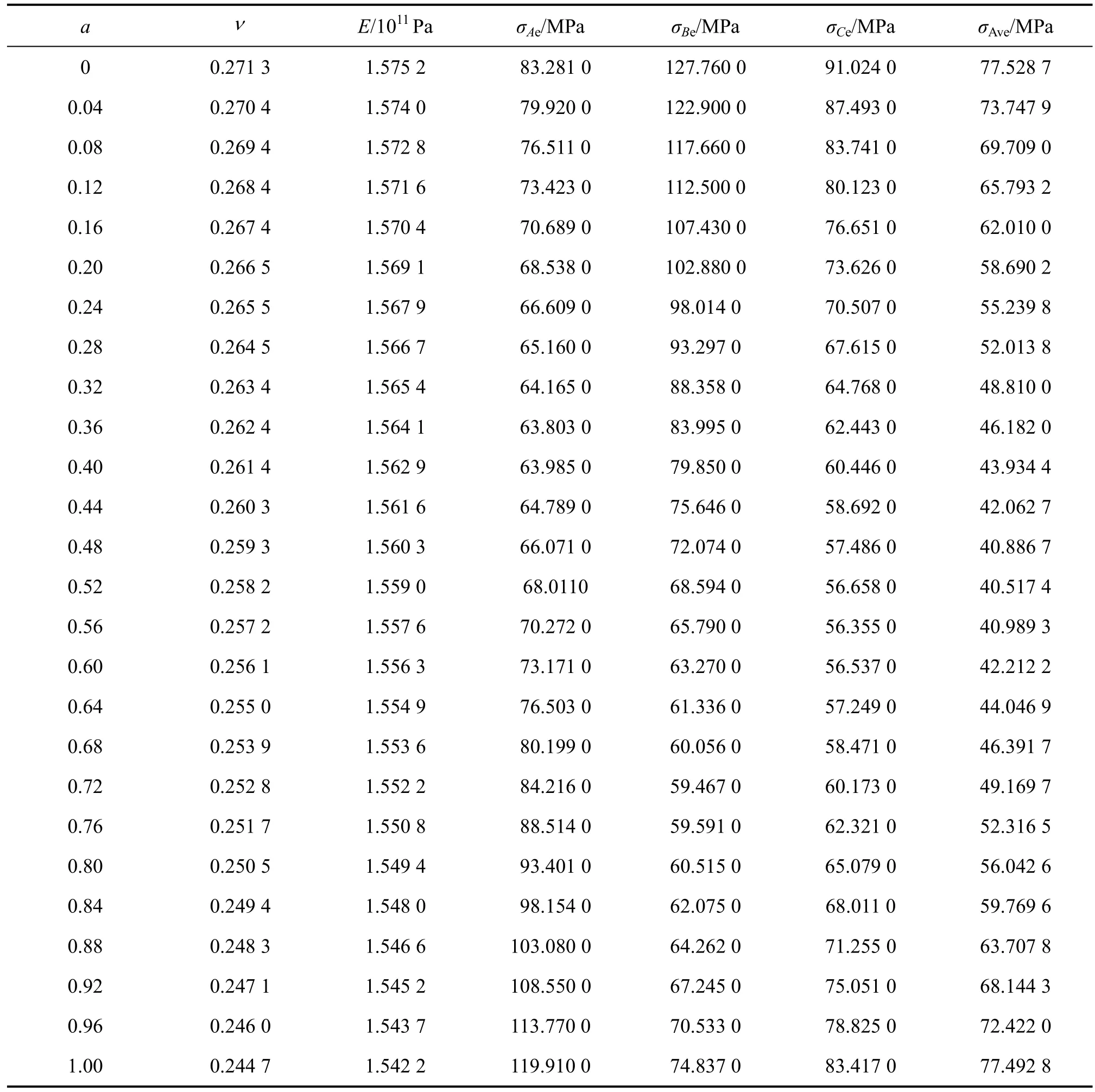
表2 颗粒边界层的弹性参数、平均等效应力及3点等效应力Table 2 Elastic parameters, equivalent stresses of average and three points at grain boundary

1.3 应力等值线计算结果

由ANSYS软件计算的应力解均采用节点解，应力单位为Pa。在800 ℃和1.6 GPa静水压下，当b为0.5，a为0.5时，等效应力等值线图且根据对称性扩展至整个模型的等效应力场如图2所示。从图2可知：在静水压下，透辉石与镁橄榄石矿物颗粒之间的界面上存在应力集中现象，颗粒边界层的应力分布不均匀。根据表2 ，依次计算颗粒边界层具有不同弹性模量和泊松比时的节点等效应力等值线图。图3所示是a分别为0.1和0.5时由计算模型扩展至整个模型的边界层等效应力等值线图。

1.4 结果分析

从采用的节点解的等效应力等值线图可知：矿物颗粒边界层的弹性模量和泊松比不同，其应力分布也不同。为了找出其中的变化规律，取矿物颗粒边界层2 402个节点，计算其平均等效应力，并在矿物颗粒边界层取A，B和C3点，此3点在计算模型中的坐标依次为(0.085 0，0.105 0，0.100 0)，(0.085 0，0.100 0，0.100 0)和(0.085 0，0.102 5，0.100 0)，单位为 mm。随着体积模量系数a及其相应的弹性模量和泊松比的变化，计算得到的平均等效应力以及A，B和C3点的等效应力部分解见表2。

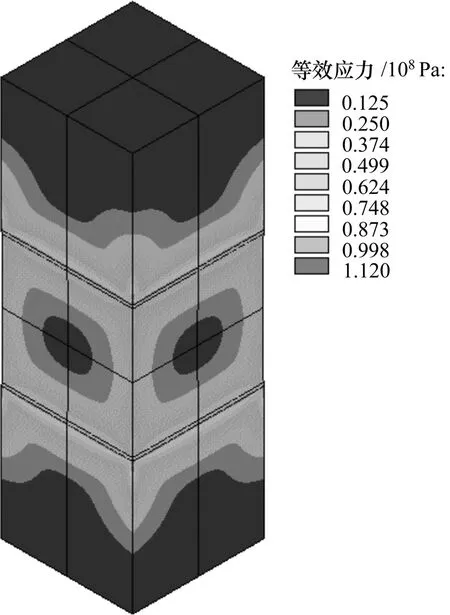
图2 整体模型等效应力等值线图Fig.2 Equivalent stress contour plot of whole model when a=0.5 and b=0.5

图3 矿物颗粒边界等效应力等值线图Fig.3 Equivalent stress contour plot at mineral grain boundaries

据表2中的数据做出散点图并进行高斯曲线拟合(见图4(a))，平均等效应力以及A，B和C3点的等效应力σe与体积模量系数a的关系满足高斯分布函数方程：

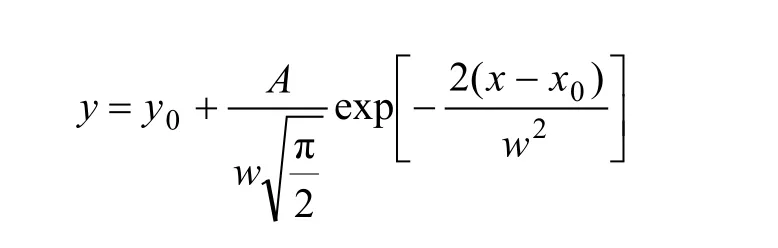
拟合的高斯分布函数的相关系数R和方程特征参数如下：

σAe与a的关系中，R2=0.999 77，w=1.41，A=−289.40，y0=228.12，x0=0.36；

σBe与a的关系中，R2=0.999 57，w=1.02，A=−133.80，y0=164.65，x0=0.73；

σCe与a的关系中，R2=0.998 23，w=0.90，A=−74.02，y0=121.91，x0=0.55；

σAve与a的关系中，R2=0.998 22，w=0.78，A=−63.25，y0=105.41，x0=0.51。

将平均等效应力以及A，B和C3点的等效应力与颗粒边界层弹性模量的散点图进行拟合，拟合结果也符合高斯分布，如图4(b)所示。拟合方程的相关系数R和特征参数如下：

σAe与E的关系中，R2=0.999 81，w=0.04，A=−4.99，y0=173.30，x0=1.56；

σBe与E的关系中，R2=0.975 10，w=0.02，A=1.32，y0=63.26，x0=1.58；

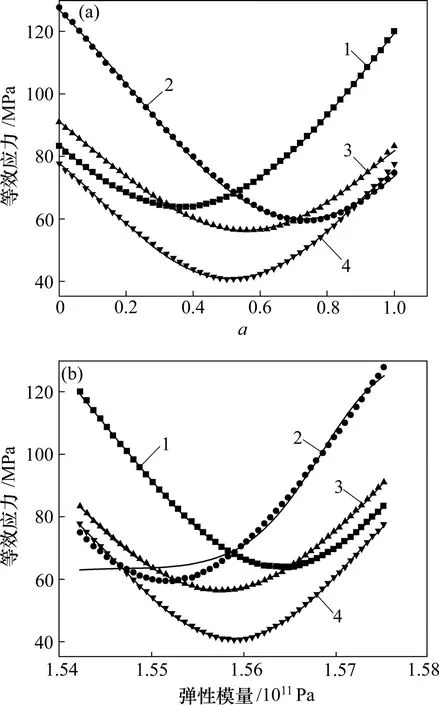
图4 颗粒边界平均等效应力及A，B和C 3点等效应力曲线图Fig.4 Equivalent stress curves of point A, B, C and average at grain boundary

σCe与E的关系中，R2=0.999 91，w=0.04，A=−3.98，y0=145.27，x0=1.56；

σAve与E的关系中，R2=0.999 27，w=0.03，A=−2.23，y0=108.10，x0=1.56。

2 讨论

岩石、矿物若长时间处于高温高压并有差应力下会发生蠕变变形，但对于某一特定的矿物或岩石，在不同温度和压力下，人们还不了解应变率与应力的确切关系式，如橄榄石在高温下的蠕变机制在岩石圈温度 900～1 200 ℃范围内与温度高于 1 200 ℃时不一样[23]，后者应变率与差应力呈幂律关系，而前者却呈指数关系。在一定温度和压力下，组成岩石的不同矿物颗粒之间可能发生化学反应或部分熔融，在矿物颗粒接触界面上生成新的物质，进而形成薄薄的矿物颗粒边界层或直接由不同矿物以某一比例组成的过渡层。由于边界层物质可能不同程度地含有孔隙[24]甚至熔体[25]等，即使是在相同的温度和压力下，其边界层的弹性参数也可能不一样[26]，从而影响岩石、矿物的力学性质与变形机制。

镁橄榄石、透辉石的熔点都高于1 000 ℃，本研究中采用800 ℃和1.6 GPa静水压条件，在上地幔—下地壳温度、压力条件范围内，两矿物集合体在加静水压瞬间必然会发生弹性变形。通过三维模拟计算，在完全弹性变形阶段(如图2 所示)，两矿物颗粒边界层有应力集中现象。为了找出其边界层应力分布规律，设定颗粒边界层为两矿物的过渡层，边界层(过渡层)的体积模量为两矿物的体积模量乘以1个变化系数后之和，依此计算得到边界层不同的泊松比、弹性模量，进行多次模拟计算，部分结果见表2。图4中拟合的高斯曲线方程，相关系数R2都在0.95以上。在静水压力作用下，当立方体结构的镁橄榄石与透辉石集合体在其颗粒内部与颗粒边界都处于完全弹性变形时，颗粒边界层的平均等效应力及其空间任意点的等效应力与颗粒边界层组分矿物的体积模量系数、边界层组成物质的弹性模量之间具有高斯分布规律，并且不同位置点拟合的高斯分布函数特征参数不同，说明在静水压下，处于弹性变形阶段的矿物颗粒边界层内部应力分布不均匀。

不同矿物颗粒边界的应力分布规律有助于从力学上解释岩石、矿物在高温高压下的一些微观变形特征，如位错、扩散、边界迁移、滑移等以及由矿物颗粒边界引起岩石、矿物的弹性波速的变化。岩石中的颗粒边界对应力敏感而导致在钻孔周围存在弹性波速与应力之间的非线性变化[27]；静水压试验测出P 波速度随着主应力(静水压)的增大呈非线性上升[28]；Ji等[29]通过对大别—苏鲁超高压变质岩层的研究，得出P波速度−压力非线性曲线可以用1个有4个参数的指数方程进行描述，并赋予了这4个参数的物理意义。尽管本文的模拟计算是在理想状态下进行的，只是模拟计算静水压力下立方体结构的镁橄榄石与透辉石集合体在完全弹性变形时的边界应力，但可以类推为静水压下2种立方体结构的不同矿物的集合体。计算结果表明：在矿物颗粒边界应力集中，边界层应力分布不均匀，颗粒边界层的等效应力与边界层组成物质的弹性模量之间具有高斯分布函数关系。这对于具有确切物质组成的矿物颗粒边界，根据其拟合的高斯分布函数进行化简，可以得到与弹性模量相对应的等效应力，再根据弹性模量与弹性波速的计算公式[30]，可以推导出静水压力下岩石、矿物内部的等效应力与弹性波速的关系式。

在高温高静水压下，立方体结构的2种不同矿物颗粒边界应力的这种高斯分布规律为矿物颗粒边界效应的研究提供了依据。在今后的研究中，有必要考虑非静水压条件、矿物颗粒内部及边界有蠕变变形、矿物颗粒之间的接触有摩擦和间隙等情况，并结合高温高压实验、分子动力学模拟精确确定计算模型中的弹性模量、泊松比等参数，进而综合模拟研究矿物颗粒边界效应对岩石的力学性质与变形机制的影响。

3 结论

(1) 在高温高静水压下完全弹性变形时，2种立方体结构的不同矿物颗粒边界具有应力集中现象，颗粒边界层内部应力分布不均匀。

(2) 2种立方体结构的不同矿物集合体在高温高静水压下完全弹性变形时，过渡边界层的等效应力与其组分矿物的体积模量系数及其组成物质的弹性模量之间具有高斯分布规律。

致谢：本文得到了湘潭大学机械学院龚曙光教授、中国科学院地质与地球物理所伍向阳研究员、中国地震局地质研究所何昌荣研究员、湘潭大学材料与光电物理学院毛卫国副教授的指导，在此一并表示衷心感谢！

[1] Holtzman B K, Kohlstedt D L, Zimmerman M E, et al. Melt segregation and strain partitioning: implications for seismic anisotropy and mantle flow[J]. Science, 2003, 301(5637):1227−1230.

[2] Holtzman B K, Kohlstedt D L, Morgan J P. Viscous energy dissipation and strain partitioning in partially molten rocks[J]. J Petrol, 2005, 46(12): 2569−2592.

[3] JI Shao-cheng, ZHAO Ping-lao, XIA Bin. Flow laws of multiphase materials and rocks from end-member flow laws[J].Tectonophysics, 2003, 370(1/4): 129−145.

[4] HE Chang-rong. ZHOU Yong-sheng, SANG Zu-nan. An experimental study on semi-brittle and plastic rheology of Panzhihua gabbro[J]. Science in China: Series D, 2003, 46(7):730−742.

[5] Dimanov A, Dresen G, Wirth R. High-temperature creep of partially molten plagioclase aggregates[J]. J Geophys Res, 1998,103(B5): 9651−9664.

[6] Jaoul O, Raterron P. High-temperature deformation of diopside crystal 3. influences ofpO2and SiO2precipitation[J]. J Geophys Res, 1994, 99(B5): 9423−9439.

[7] MEI Sheng-hua, Kohlstedt D L. Influence of water on plastic deformation of olivine aggregates 1. diffusion creep regime[J]. J Geophys Res, 2000, 105(B9): 21457−21469.

[8] MEI Sheng-hua, Kohlstedt D L. Influence of water on plastic deformation of olivine aggregates 2. dislocation creep regime[J].J Geophys Res, 2000, 105(B9): 21471−21481.

[9] Hier-Majumder S, Anderson I M, Kohlstedt D L. Influence of protons on Fe-Mg interdiffusion in olivine[J]. J Geophys Res,2005, 110, B02202, doi: 10.1029/2004JB003292.

[10] Hier-Majumder S, Mei Sheng-hua, Kohlstedt D L. Water weakening of clinopyroxenite in diffusion creep[J]. J Geophys Res, 2005, 110, B07406, doi: 10.1029/2004JB003414.

[11] 赵延林, 曹平, 文有道, 等. 渗透压作用下压剪岩石裂纹损伤断裂机制[J]. 中南大学学报: 自然科学版, 2008, 39(4):838−845.ZHAO Yan-lin, CAO Ping, WEN You-dao, et al. Damage fracture failure mechanism of compressive-shear rock cracks under seepage pressure[J]. Journal of Central South University:Science and Technology, 2008, 39(4): 838−845.

[12] 杨振涛, 宁杰远, 赵永红. 多矿物岩石流变性的有限元计算[J]. 岩石学报, 2004, 20(6): 1469−1476.YANG Zhen-tao, NING Jie-yuan, ZHAO Yong-hong. Finite element computation of rheology for multi-mineral rocks[J].Acta Petrologica Sinica, 2004, 20(6): 1469−1476.

[13] Madi K, Forest S, Cordier P, et al. Numerical study of creep in two-phase aggregates with a large rheology contrast:implications for the lower mantle[J]. Earth Planet Sci Lett, 2005,237(1/2): 223−238.

[14] Becker J K, Bons P D, Jessell M W. A new front-tracking method to model anisotropic grain and phase boundary motion in rocks[J]. Comput Geosci, 2008, 34(3): 201−212.

[15] Hier-Majumder S, Leo P H, Kohlstedt D L. On grain boundary wetting during deformation[J]. Acta Mater, 2004, 52(12):3425−3433.

[16] Hiraga T, Anderson I M, Kohlstedt D L. Grain boundaries as reservoirs of incompatible elements in the Earth’s mantle[J].Nature, 2004, 427: 699−703.

[17] de Ronde A A, Stünitz H. Deformation-enhanced reaction in experimentally deformed plagioclase-olivine aggregates[J].Contrib Mineral Petrol, 2007, 153(6): 699−717.

[18] Yoshino T, Takei Y, Wark D A, et al. Grain boundary wetness of texturally equilibrated rocks, with implications for seismic properties of the upper mantle[J]. J Geophys Res, 2005,110(B08205), doi: 10.1029/2004JB003544.

[19] Takei Y. Deformation-induced grain boundary wetting and its effects on the acoustic and rheological properties of partially molten rock analogue[J]. J Geophys Res, 2005, 110(B12203),doi: 10.1029/2005JB003801.

[20] 桑祖南, 夏斌, 周永胜, 等. 含矿辉长岩液态不混溶作用实验研究[J]. 中国科学: D辑, 2003, 33(4): 353−361.SANG Zu-nan, XIA Bin, ZHOU Yong-sheng, et al. Experimental study of ore gabbro liquid immiscibility[J]. Science in China:Series D, 2003, 33(4): 353−361.

[21] Anderson O L, Isaak D G. Elastic constants of mantle minerals at high temperature[C]//Ahrens T J. Mineral physics &crystallography: A handbook of physical constants. Washington:American Geophysical Union, 1995: 64−97.

[22] Bass J D. Elastic of minerals, glasses, and melts[C]//Ahrens T J.Mineral physics & crystallography: A handbook of physical constants. Washington: American Geophysical Union, 1995:45−63.

[23] Demouchy S, Schneider S E, Mackwell S J, et al. Experimental deformation of olivine single crystals at lithospheric temperatures[J]. Geophys Res Lett, 2009, 36(L04304), doi:10.1029/2008GL036611.

[24] Ciz R, Siggins A F, Gurevich B, et al. Influence of microheterogeneity on effective stress law for elastic properties of rocks[J]. Geophysics, 2008, 73(1): E7−E14.

[25] JIN Zhen-ming, Green H W, ZHOU Yi. Melt topology in partially molten mantle peridotite during ductile deformation[J].Nature, 1994, 372: 164−167.

[26] WANG Qian, JI Shao-cheng, SUN Sheng-si, et al. Correlations between compressional and shear wave velocities and corresponding Poisson’s ratios for some common rocks and sulfide ores[J]. Tectonophysics, 2009, 469(1/4): 61−72.

[27] Sayers C M. Effect of borehole stress concentration on elastic wave velocities in sandstones[J]. Int J Rock Mech Min Sci, 2007,44(7): 1045−1052.

[28] Scott T E. The effects of stress paths on acoustic velocities and 4D seismic imaging[J]. The Leading Edge, 2007, 26(5):602−608.

[29] JI Shao-cheng, WANG Qian, Marcotte D, et al. P wave velocities,anisotropy and hysteresis in ultrahigh-pressure metamorphic rocks as a function of confining pressure[J]. J Geophys Res,2007, 112(B9), doi: 10.1029/2006JB004867.

[30] 谢鸿森. 地球深部物质科学导论[M]. 北京: 科学出版社,1997:55−57.XIE Hong-sen. Introduction to materials science of the earth’s interior[M]. Beijing: Science Press, 1997: 55−57.