时间序列模型在税收预测中的应用＊

□ 张新波

(湖南韶山市国税局,湖南 韶山 411300)

时间序列模型在税收预测中的应用＊

□ 张新波

(湖南韶山市国税局,湖南 韶山 411300)

以往对未来税收收入预测主要采用对重点税源企业调查汇总的方式,这种预测方法工作量大且存在一定弊端,以韶山市税收收入为例用回归的思想将时间序列的方法应用于税收预测,能对未来税收预测提供一定参考。

税收预测;时间序列模型;应用

如何对未来税收进行合理预测,这是制定未来税收任务应该首先解决的问题。以往对一个地区税收预测主要是通过对重点税源调查,将数据进行整理汇总,来推测出一个地区税收的总收入,这种处理方法工作量大而且缺乏对纳税整体的把握,当一个地区税源比较复杂重点税源企业税收不能占绝对优势时,汇总预测精度往往不够高。而现有很多政策还受计划体制的影响,税收任务的制定很多时候都是行政式的,不能合理反映事物发展的趋势。

一个地区经济发展过程从较长时间看,在市场机制的作用下呈现比较明显的趋势,这为预测提供了依据;从短期看,由于受到宏观政策、市场即期需求变化等不确定因素影响,表现出一定的波动,这对预测造成了困难。目前预测经济运行一般采取的是时间序列方法,比较经典的有灰色理论、生长曲线、AR IMA模型等,这些模型对经济长期趋势一般把握比较准。在东部个别沿海发达城市已经将时间序列分析方法用作对经济发展指标的预测,并取得了很好的效果。当然在实际应用中选取何种时间序列模型要根据数据本身的特点作出具体分析。本文以韶山市税收收入为例,通过观察韶山市 2001至 2009年国税收入数据 (不含车购税和海关代征),用回归的思想,通过最小二乘法将时间序列指数曲线模型引入税收分析预测,希望能为以后税收政策和计划的制定提供一定参考。

一 最小二乘思想的简单介绍

最小二乘法 (又称最小平方法,Ordinary least Squares,简记OLS)是一种数学优化技术。以误差的平方和最小为准则,根据观测数据,估计线性模型中未知参数的一种基本参数估计方法。它的基本思路是选择估计量使模型(包括静态或动态的,线性或非线性的)输出与实测输出之差的平方和达到最小。这种求误差平方和的方式可以避免正负误差相抵,而且便于数学处理 (如用误差的绝对值就不便于处理)。最小二乘估计能使参数的真实值和估计值相差达到最小,而且在一定意义上没有比最小二乘估计更好的估计,该估计理论上比较优良,使用范围也比较广。

对模型参数的求解思想是借助数学方法实现的,其数学解释和实现过程相关参考文献都有详细介绍,这里不再体现。本文主要是运用可化为线性的曲线拟合问题,通过观测历年韶山税收数据的散点图,将模型y=aebx用变量替换Y=lny,X=x,将函数化为线性函数:y=lna+bx,从而求出预测方程,这里借助统计软件来计算参数的值,具体推导求解过程比较繁琐,此处省去中间过程。

二 回归模型在我市税收领域的应用

(一)数据的来源和描述

将韶山 2001-2009年税收收入数据整理得下表 1,并按数据次序作图 1。

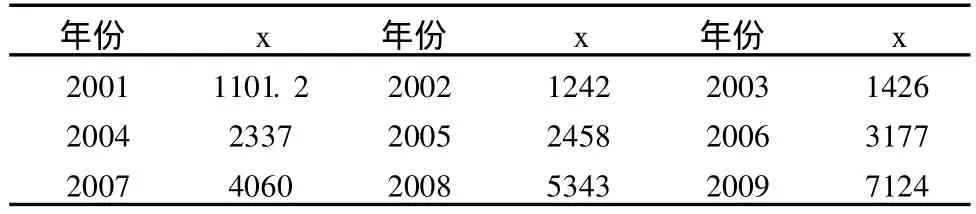
表一 韶山市 2001-2009年税收收入 (单位:万元)

通过图 1可以看出韶山今年税收具有明显长期上升的趋势,而且上升曲线很光滑,很适合做平滑曲线模型。这里通过对比选择了指数曲线,指数曲线中参数的求法运用的是最小二乘法,求解和作图的过程借助 SPSS统计分析软件,这里不再对求解的过程做数学推导,直接给出指数曲线的预测方程和拟合优度R2(0≾R2≾1)。

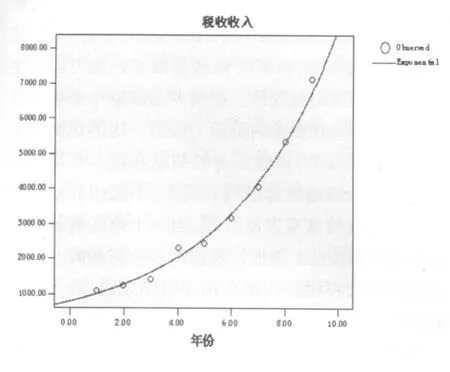
图一 韶山历年税收时序图

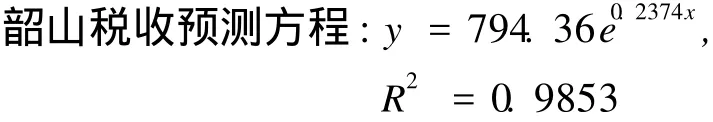
(二)对统计模型的的检验评判

统计分析中判断一个模型的好坏主要是通过假设检验来实现的,这里我们从三个角度来对模型作出评判:

1、判断数学模型的好坏,可借助拟合优度 R2来判断,R2越趋近于 1越好。R2越大,说明回归曲线拟合程度越好;R2越小,说明回归曲线拟合程度越差。由上可知,通过考察 R2的大小,我们就能粗略地看出回归线的优劣。

2、再次我们可以通过方差分析表来判定

表二 ANOVA

选用 95%的置信区间,做出假设检验。该指数模型的 F值为 467.763,显著水平小于 0.0001,说明这个回归方程具有统计意义。

3、可以通过对模型的回判,将历史真实值和预测值进行对比来判定模型的好坏。具体对比会在表2中体现。

三 预测和结论

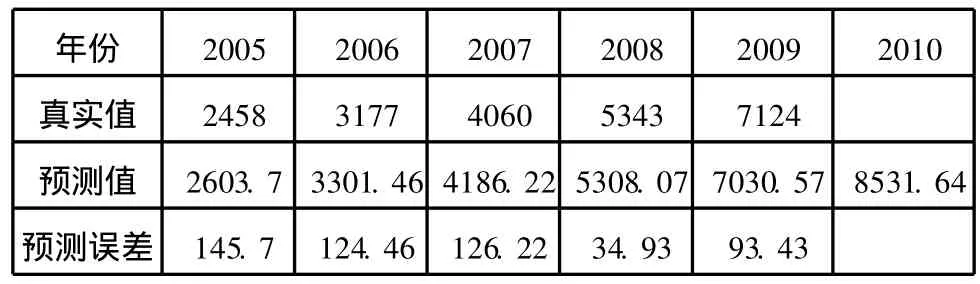
表三 韶山税收预测 (单位:万元)

通过预测值与真实值的对比可以看出模型的拟合效果还是比较好的,我们将 2010年参数代入预测方程,得出 2010年韶山税收收入为 8531.64万元。

时间序列预测方法是一种重要的预测方法,其模型比较简单,对资料的要求比较单一,在实际中有着广泛的适用性。但在应用中,应根据所要解决的问题及问题的特点等方面来综合考虑并选择相对最优的模型。

在实际运用中,由于税收收入总额的特殊性,时间序列模型提供了较好的预测效果,从表 2中不难看出,预测值和实际值之间的误差较小,说明回归方程的预测结果还是比较理想的。但时间序列模型随着预测的延长,预测误差会逐渐增大,这也是很多时间序列模型的缺陷。尽管如此与其他的预测方法相比,其预测的准确度还是比较高的,尤其在短期预测方面。

四 时间序列模型在我市税收领域应用的一些推广

(1)预测、决策功能。时间序列模型不仅可以对本市的税收做出预测,也可以将其推广到对各地区、各部门和各行业经济指标的预测。通过采集相应真实的指标数据,计算出对应参数。一方面对未来的发展趋势作出合理预测,另一方面为做出科学决策提供依据。

(2)这里可以将相应的统计预测方法应用于各个重点税源企业,通过观察企业各个时期生产指标数据和税收数据建立相应的时间序列模型,计算出对应参数,对企业未来的生产和税收数据作出预测。当企业上报的生产和税收数据与预测数据 (假设检验中的置信区间)出现较大偏差时,相关部门应及时深入企业调查,了解企业生产真实情况,降低纳税风险。同时也可以对税务部门内部税收数据做出相应的时间序列分析,如前所述,一个企业或地区经济发展在一定时期内呈现一定趋势,而且在短期内发生严重背离发展趋势的概率比较小,因此,一个地区税收收入在短期内突然呈现大幅增长,相关上级部门应及时了解,对该地区情况采取相应措施,及时控制和降低风险,同时该理念也可以引入对一个单位和干部相应的绩效考核中,避免不确定的非经济因素对税收收入的控制和影响。

五 模型的优点和不足

时间序列模型的优点在于它是通过对历史数据的研究来建立模型,得出经济发展的趋势,并对未来数据作出预测。而以前的预测主要是通过调查、整理然后汇总数据得到的,对于大的经济体,全面调查是不可能实现。

在使用最小二乘法时,我们并未要求得到的拟合曲线一定要经过所有的样本点,而只是要求了总偏差最小。当实际问题要求拟合曲线必须经过样本点时,我们可以选择其他的模型,应用数值逼近中的插值法,这种方法可以很轻松实现。

当然这里只是从数量经济学角度采用统计模型对韶山未来税收进行预测,模型的预测的准确性还依赖:

1、国家的经济形势是否平稳,模型的建立难以顾及突发经济危机对我市企业发展的影响,例如2008年世界经济危机对我国各省市经济发展的影响。当然经济发展过程中某些季节或者周期性的因素对经济发展数据也会造成影响,这些影响我们可以通过具体情况选择更合适模型将此因素消除。

2、是否有纳税大户从我市突然撤出或者进入,这也将极大影响我市的税收结构。例如韶山旭宁科技发展有限公司 2009年 11、12月税收额随着销售额的增长大幅度提升,对整个韶山全年税收收入影响很大,尽管很多地区受金融危机的影响税收收入下降,但韶山的税收仍然保持良好的趋势。

3、国家政策因素对税收的影响。国家通过调节税收政策对某些行业发展的扶持和限制都将对未来税收结构产生显著影响。例如今年将电力预征率从1.4%上调至 2.8%,电力企业的税收额在以往基础上肯定会出现同比例的上升,这都将影响到模型的预测的精度。

4、不确定的人为因素的影响。在现有体制下,人为因素在很大程度上会对税收收入产生很大影响,统计模型大都是刚性的,很难克服人为因素对其产生的不利影响,很多时候这些因素甚至可以完全决定一个模型的有效性。如很多地区多年来税收任务的制定都是在原来的基础上按照一定的比例制定来年的税收任务,税收任务的制定在很大程度上是为了满足上级地区总的税收需要,不能很好地体现经济与税收的真实发展情况,当一个地区税收收入提前达到或接近上级地区要求的税收任务时一些人为的因素会将税收控制在相应范围之内;而当税收收入小于当年税收目标时,一些人为因素又会通过一些措施增加部门税收收入,不至于使税收收入过大偏离上级要求的税收计划,这都是统计模型遇到的尴尬之处,如何使税收很好地反映和促进一个地区经济的和谐发展,这都是相关部门在很多方面需要思考的问题。

[1]陈家鼎,刘婉如,汪仁官.概率统计讲义[M].北京:高等教育出版社,1980.

[2]卢纹岱.SPSS forW indows统计分 [M].北京:电子工业出版社, 2006.

[3]刘新利,税收分析概论[M].北京:中国税务出版社,2000.

[4]湖南省国家税务局.湖南税务统计 2005[R].

F810.42

A

1008-4614-(2010)04-0030-03

2010-05-10

张新波(1982-),男,河南三门峡人,湘潭韶山市国税局副主任科员。