纵弯复合模式直线型超声波电机研究与实验
翁志刚
(皖西学院机械与电子工程系,安徽六安 237012)
纵弯复合模式直线型超声波电机研究与实验
翁志刚
(皖西学院机械与电子工程系,安徽六安 237012)
研究了纵-弯模式直线型超声波电机的驱动机理,设计制作了一台输出大力矩的纵-弯复合模式直线型超声波电机样机,并进行了实验测试,绘制了在一定的预压力、预紧力和驱动电压时候激励频率与速度的关系曲线,在一定的预紧力、预压力和激励频率下驱动电压与速度的关系曲线以及预紧力、激励频率和驱动电压一定情况下预压力与速度的关系曲线,并对实验结果进行了分析。实验结果表明,这种新型结构电机充分体现了超声波电机良好的性能特点,特别是能输出较大的转矩,具有良好的应用前景。
超声波电机;直线;纵-弯复合
引言
超声波电机(Ultrasonic Motor,USM)是一种基于压电陶瓷逆压电效应原理的新型电机。其工作原理是将超声频率的电信号加在压电陶瓷片上激发对应频率的振动,通过耦合或者复合在定子端部质点形成纳米级的椭圆振动轨迹,质点的椭圆运动在定转子之间有一定预压力的前提下,转子被定转子之间的摩擦力所驱动。与传统电磁电机相比,它具有响应快、低速大转矩、断电自锁、定位精度高、无电磁干扰、结构简单等优点[1]。
以往超声波电机基本上是单一模式的,例如纵向振动模式、扭转振动模式或弯曲振动模式。这种电机具有结构简单、重量轻、频率低、频率范围宽等特点,在一些新的超声应用中,对振动能量的传播方式及作用形式提出了不同的要求,例如超声旋转加工需要扭转或纵-扭复合模式,超声马达需要纵-弯或纵-扭复合模式,而外科手术用的超声手术刀,则需纵-弯复合模式中的弯曲振动产生有效的侧向分离力纵向振动完成组织的切除任务。另外,在一些应用的场合我们需要产生直线的运动,而利用传统的电磁电机要获得直线运动需要中间的转换装置(链条、钢丝绳、传动带、齿条或丝杆等),这样就使得整个设备存在着体积大、效率低、精度低等问题,鉴于此,本文以纵-弯复合模式直线型超声波电机作为研究对象,希望能为该类型的电机研究积累一点经验。
1 电机驱动机理与电机结构设计

图1 定子结构示意图
本次设计的超声波电机采用螺栓紧固的兰杰文(Langevin)振子结构,如图1所示,用一根螺栓将前盖板、陶瓷片、后盖板以及电极紧固在一起,这样的结构相比较黏结的结构不仅装配起来方便,而且可以通过螺栓来调节预紧力。中间的四片陶瓷片的极化方向和摆放方式如图2所示,其中弯曲振动陶瓷片极化方向沿厚度方向,极化时两个半圆的极化方向相反,这样在陶瓷片上两边加同一激励电压时就会产生沿厚度方向一边伸长一边缩短,从而使定子产生弯曲。当这个电压产生交变时,就会使定子产生相同频率的弯曲振动。当定子越细长的时候,在定子端部的弯曲振动振幅必然也越大。纵向振动陶瓷片极化方向也是沿着厚度方向,整个圆环沿厚度方向极化方向一致,在外加交变电压的情况下,陶瓷片沿着厚度方向伸缩,使定子端部产生上下的纵振动。在两组压电陶瓷片上施加两路同频率且相位差为90°的激励电压时,定子同时产生弯曲振动和轴向纵振动,则在定子端部形成椭圆运动,从而驱动移动子做直线运动。图3所示为定子分别在纵振和弯曲振动激励下的振型示意图。如激励的两相电压相位差为90°时电机正向做直线运动,而相位差为-90°时,电机做反向的直线运动[2][3]。

图2 陶瓷片极化方向与摆放顺序

图3 定子的一阶纵振和二阶弯振振型示意图
图4所示为本次设计的纵-弯复合模式直线型超声波电机的结构简图,一根螺栓将前盖板、陶瓷片和后盖板紧固在一起形成兰杰文振子,并固定在定子固定底座上。为了保证导轨左右做直线运动,陶瓷片摆放的时候弯曲振动的片的分极分界线应该垂直图4所示的纸面。图中前盖板设计成圆台形状的变幅杆,这样可以放大振幅从而获得较大的驱动力。而且采用这种连续变截面的变幅杆比突变截面的变幅杆在波以及能量的传输的过程中具有较小的损耗[4][5]。

图4 设计电机结构简图
2 电机样机驱动实验
根据图4的结构设计制作了一台样机。并与驱动电源、直流电源、示波器等组成试验平台。直流电源提供0-30V的直流电压,超声波驱动电源输出频率15-100KHz的交变信号,示波器用来监视电源输出的信号的波型、频率、峰-峰值等参数。
2.1 激励频率-速度输出特性
在电源输入电压12V、预压力为4.9N的条件下,测试了样机的激励频率-速度特性。实验测试曲线如图5所示。
从图5的曲线可以看出:电机的谐振频率为25. 82k Hz附近,此时速度最大。输入信号频率偏离谐振频率越大,速度越低,近似的成正态分布。但设计频率与实际测试的系统共振频率有一定的误差,主要是由于加工与装配等因素引起的,预紧力的大小对电机谐振频率也有一定的影响。

图5 样机的激励频率-速度曲线图

图6 样机的驱动电压-速度特性曲线图
2.2 驱动电压-速度特性
该项实验是在频率为25.82k Hz与预压力为4. 9N的条件下测试电机的输出速度随输入电压变化的情况。通过电压调节控制电机输出速度的变化,测得的输出速度和电源输入电压之间的关系曲线如图6所示。由图可见,电机的输出速度随驱动电压变化趋势有明显的近似线性关系。驱动电压增大,输出的速度随之增大。根据压电陶瓷材料的性质,由压电系数可知,当加在它上面的电压增大时,其变形也增大,使得整个超声振动系统的振幅也随之增大,引起弯曲挠度增大,从而输出速度也会增大。
2.3 预压力-速度特性
超声波电机定子和转子的接触状态一般取决于定转子间预压力大小和定子表面激励的纵振动振幅。预压力是影响超声波电机输出性能的重要参数之一。在电源输入电压为12V及输入信号频率25.82kHz条件下测试了样机的输出速度与预压力关系,如图7所示。

图7 预压力-速度曲线图
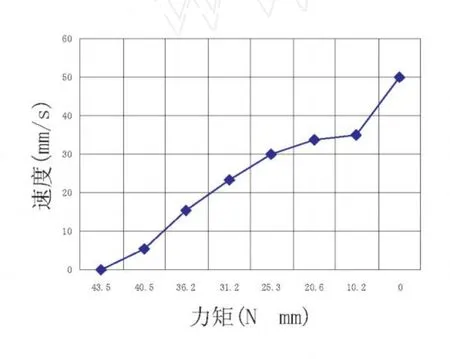
图8 转矩-速度曲线图
电机速度随着预压力的增大而上升,但当预压力大于一定值时,电机速度随着预压力的增大而下降。可见,预压力对超声波电机的输出特性有较大的影响。每一种超声波电机的最高输出速度对应不同的预压力最佳值。
2.4 力矩-速度特性
图8所示的是电机样机在激励频率为 25. 82KHz,电源输入电压为12V,预压力为4.9N的情况下电机样机输出力矩与速度之间的关系曲线。从图8可看出,当电机样机输出的转矩增大时速度减小,直至速度为零得到上述输入状态下的堵转力矩为49.8N·mm。空载的时候电机的速度最大,电机工作的时候可以计算出摩擦力f=μN=0.403×4.9= 1.97N,其中μ为滑动摩擦因数,其大小与材料、表面粗糙度、压力及对滑动速度有关。可见该类型电机可以输出比较大的转矩。
3 实验结果分析
超声波电机的性能既受到内部因素,如本身结构、材料等方面制约,同时也与外部因素如环境温度、负载情况、激励控制密切相关。本文测试实验探讨了几个输入参数(激励频率、驱动电压、预压力等)对电机输出性能的影响。
3.1 激励频率分析
由图5中可以看出,在驱动电源信号的激励频率由小到大变化的过程中,超声波电机的输出速度近似成正态分布的规律。超声波电机速度的最大值对应系统的共振频率处;偏离共振频率时,纵振动幅值减小,从而使超声波电机输出速度降低。驱动电源的激励频率越接近谐振频率,速度越快,当达到共振频率时,速度最大。从频率关系曲线图可以看出,随着频率的变化,超声波电机的速度变化比较明显,这表明利用频率调节超声波电机的速度的可调范围较小,约为1KHz范围内。
3.2 驱动电压分析
从电压-速度特性曲线可以看出随着输入电压的增加,输出的速度也随之增大,输出的速度随电压值呈现近似线性变化关系,这是由于电压增大,压电陶瓷的逆压电效应增强,振动幅值增大,但压电陶瓷片的耐压一定的限度,同时电源的变压器也有一定的电压上限,所以电压变化有一个允许的范围。由图5中可以看到,在一定的范围内,控制驱动电压可以近似线性地控制电机的速度。
3.3 预压力分析
超声波电机的定、转子之间所加预压力的大小直接影响到超声波电机的运行性能和输出特性。当预压力太大时,电机不能正常启动;预压力太小,定、转子之间的摩擦力较小,达不到电机理想的输出效果。预压力分布的不均匀会使摩擦界面的接触情况随时间变化,产生较大的颤振和噪声,造成输出速度和力矩的不理想。在保证输入电压、驱动频率不变的条件下,不同的预压力有不同的输出速度,输出速度随预压力变化存在一个最大值。另外,预压力越大,所需的驱动电压值也越大,输出的速度才能增大。预压力和电压这两种因素相互之间是有影响的。通过调整使两因素达到最合理的匹配,可以获得较好的输出特性。
综合上述分析可知,预压力存在一个最佳范围,要使超声波电机高效、稳定工作,需要合理调节所施加的预压力值,预压力的最优值在超声波电机设计时应给予充分的重视。
4 结束语
本文在研究了纵-弯模式超声波电机的驱动机理的基础上,设计制作了一台纵-弯复合模式直线型超声波电机的样机,并进行了实验测试,绘制了在一定的预压力、预紧力和驱动电压时候激励频率与速度的关系曲线,在一定的预紧力、预压力和激励频率下驱动电压与速度的关系曲线以及预紧力、激励频率和驱动电压一定情况下预压力与速度的关系曲线,并对产生的实验结果进行了理论分析,实验结果表明,这种新型结构电机充分体现了超声波电机良好的性能特点,特别是能输出较大的转矩,具有实际的应用前景。
[1]彭海军,王德石,杜贻群.压电超声微马达的研究新进展[J].机械设计与制造,2009,6(6):109-111.
[2]陈强,胡敏强,金龙,等.弯纵复合大推力直线超声波电机[J].电工技术学报,2007,22(11):35-40.
[3]原林.纵-弯振动换能器共振特性及有限元仿真[J].甘肃联合大学学报(自然科学版),2008,11(6):38-42.
[4]王时英,吕明,轧刚.圆锥过渡复合变幅杆动力学特性研究[J].太原理工大学学报,2007,38(2):95-97.
[5]姚志远,杨东,赵淳生.杆结构直线超声电机的结构设计和功率流分析[J].中国电机工程学报,2009,29(24):56 -60.
Research on Linear Ultrasonic Motor Using Longitudinal-Flexural Modes
WENG Zhi-gang
(Mechanical and Electronic Engineering Department,West Anhui University,L u’an237012,China)
The paper studied the driven mechanism longitudinal-bending mode ultrasonic motor,designed a longitudinal-bend complex model linear ultrasonic motors,and conducted laboratory tests have drawn a certain pre-pressure,preload,and drive voltage when the excitation frequency and the velocity curve,in a certain preload,pre-stress and motivate frequency drive voltage and speed curves as well as the preload force,excitation frequency and driving voltage under certain circumstances,the pre-pressure and velocity curve and the experimental results were analyzed,the results show that the new structure fully reflects the motor performance characteristics of ultrasonic motor,especially the larger torque can be output,there is experimental application prospects.
ultrasonic motor;linear;longitudinal-flexural
TM356
A
1009-9735(2010)02-0079-04
2009-12-11
翁志刚(1984-)男,安徽六安人,皖西学院机电与工程系教师,硕士,研究方向:机械系统设计与研究。

