关于土的几种模量的讨论

郭 焱 曹瑞钠

关于土的几种模量的讨论

郭 焱 曹瑞钠

介绍了弹性模量、压缩模量以及变形模量的概念及适用条件，指出压缩模量和变形模量之间的关系公式是理论上的，其适用性有待探讨；在数值分析过程中，参数的选取应根据本构关系试算调整。

数值模拟；弹性模量；压缩模量；变形模量

0 引言

在我们进行设计或者数值模拟工作过程中，需要定义各种各样的参数，很多时候模量采用弹性模量，而勘察报告中一般只有压缩模量，变形模量也很少有单位提供，这为设计者进行数值模拟的工作带来一些不便。本文本着讨论的原则，对现行理论进行收集、整理、分析，希望为设计工作者提供一些有益的思路。

1 3种模量概述

1.1 弹性模量E（Elastic Modulus）

模量的概念基于弹性力学。在弹性力学中，一个均质体，或者说理想材料的力学性能只需要它的弹性模量和泊松比。材料在弹性变形阶段，其正应力σ和弹性正应变εd符合胡克定律，其比例系数称为弹性模量。弹性模量是材料的抗弹性变形的一个量，是材料刚度的一个指标。一般采用三轴仪进行三轴重复压缩试验，得到应力应变曲线上的初始切线模量Ei或者再加荷模量Er作为弹性模量[1]，见图1。

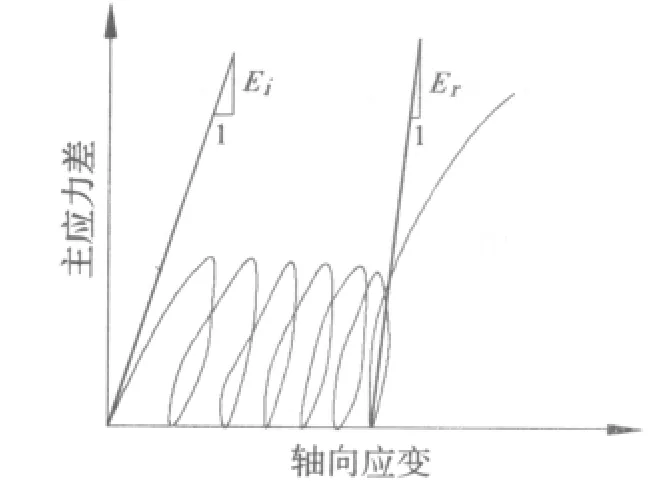
图1 室内三轴试验确定图的弹性模量

1.2 压缩模量 Es（Compression Modulus）

土的压缩模量指在侧限条件下土的垂直向应力与应变之比，是通过室内试验得到的，是判断土的压缩性和计算地基压缩变形量的重要指标之一。但是压缩模量不是个常数，首先，其大小和压力段有关系，通常的压缩模量指的是100 kPa～200 kPa压力段，这也是一个最常用的范围；其次，压缩模量的试验过程，本身就是一个排水固结的过程。

1.3 变形模量 E0（Deformation Modulus）

变形模量是根据现场荷载试验得到的，是指土在侧向自由膨胀条件下正应力与正应变的比值。从图2所示的p～s曲线可知，当荷载小于某数值时，荷载与沉降成近似直线关系，如图2中oa段，由弹性力学公式可以反算出变形模量。

图2 荷载试验p～s曲线

变形模量是把弹性模量的概念引用到土力学后衍生出的概念，在进行数值分析过程中，涉及到土体的弹性模量指的就是变形模量。

2 几种模量关系的讨论

①我国建筑地基基础设计规范指出，在计算地基变形时，地基内的应力分布可采用各向同性均质线性变形体理论。其最终变形量可按下式计算：

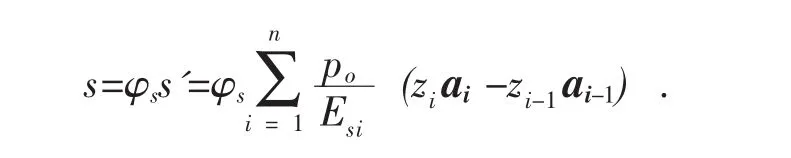
式中：s——地基最终变形量，mm；

s'——按分层总和法计算出的地基变形量；

φs——沉降计算经验系数，根据地区沉降观测资料及经验确定，无地区经验时可按规范取值；

n——地基变形计算深度范围内所划分的土层

数；

po——对应于荷载效应准永久组合时的基础底

面处的附加压力，kPa；

Esi——基础底面下第i层土的压缩模量，MPa，应取土的自重压力至土的自重压力与附加压力之和的压力段计算；

zi，zi-1——基础底面至第i层土、第i-1层土底面

的距离，m；

ai，ai-1——基础底面计算点至第i层土、第i-1层土底面范围内平均附加应力系数，可按规范采用。

由于分层总和法用的Boussinesq解是弹性解，如果按照理论的统一性，Esi用变形模量是比较合适的，但是由于变形模量参数的正确选取比较困难，而且分层总和法是基于一维压缩理论得到经验性公式的，由此规范给出了地区经验系数φs。

②土的变形模量和压缩模量都是判断土的压缩性和计算地基压缩变形量的重要指标。由于勘察报告中一般只有压缩模量，变形模量也很少有单位提供，为了建立变形模量和压缩模量的关系，在地基设计中，常需测量土的侧压力系数ξ和侧膨胀系数μ（泊松比）。

根据材料力学广义胡克定律推导求得ξ和μ的相互关系，ξ＝μ/(1－μ) 或 μ＝ε/（1＋ε）。土的侧压力系数可由专门仪器测得，但侧膨胀系数不易直接测定，可根据土的侧压力系数，按上式求得。

在土的压密变形阶段，假定土为弹性材料，则可根据材料力学理论，推导出变形模量E0和压缩模量Es之间的关系。

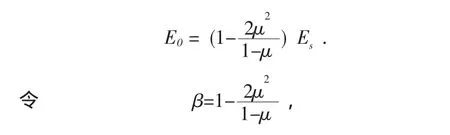
则 E0＝βEs,当 μ＝0～0.5 时，β＝1～0，即 E0/Es的比值在0～1之间变化，即一般E0小于Es。但是，实测资料表明，E0与Es的比值并不象理论得到的在0～1之间变化，而可能出现E0/Es超过1的情况，且土的结构性越强或压缩性越小，其比值越大。

③有资料指出，数值模拟中一般用E0，E（50），即达到峰值应力（应变） 50%时的割线模量。E0＝（2.0～5.0）Es。笔者认为，数值模拟采用何种参数应该因本构关系不同而有所区别，通过大量试算确定。以M-C准则为例，M-C准则是一个假设单元在弹性阶段为线弹性材料、在塑性阶段为理想塑性材料的弹塑性准则。此种假设正好与变形模量的假设相同，因此若仅计算弹性阶段的变形，采用理论公式计算变形模量是合适的；在塑性阶段，除了要考虑模量和泊松比，还要根据流动法则来确定，这时，黏聚力C、内摩擦角、剪涨角和抗拉强度都要参与进来。

3 一些结论和建议

弹性模量是弹性力学中的概念。在岩土工程中引入了弹性力学这个理论和手段，也就引进了弹性模量E。由于土体材料并不符合弹性力学的基本假定，土体的变形很大部分是不可恢复的，类似塑性变形，并且这个变形在受力开始阶段就有不可恢复部分，这样用弹性模量E的参数来衡量就概念上说不通了，因此便有了压缩模量、变形模量之说。这些概念的出现是和实际情况分不开的，并非闭门造车，因此，能够适宜的应用这些概念才是重点。本文通过整理分析，得到了一些心得。

①通过弹性力学理论得出的压缩模量和变形模量的关系是理论上的，其适用性有待探讨。

②根据各个参数试验手段不同，在土体模拟分析时，一维压缩问题推荐用压缩模量；如果是三维变形问题，推荐用变形模量。

③数值分析参数取值，应该根据本构关系不同而有所改变，同时要进行大量试算。

④造成实际中变形模量和压缩模量之比大于1，除了理论上的差别，现场试验的操作方法、土体的扰动以及试验时的排水固结条件也是重要的影响因素。

[1]高大钊主编.土质学与土力学 （第3版）.北京：人民交通出版社，2001.

[2]中华人民共和国建设部.GB50007-2002建筑地基基础设计规范.北京:中国建筑工业出版社，2002.

[3]东南大学，浙江大学，湖南大学，等.土力学.北京：中国建筑工业出版社，2005.

Discussion about Soil Modulus

GuoYan CaoRuina

This paper mainly talks about the concept of elastic modulus， compression modulus and deformation modulus，and also introduces the applicable conditions.Through this paper you can find out that the formula between compression modulus and deformation modulus is correct in theory，but may be not in practice，so in the process of numerical analysis we should choose the parameter based on the constitutive relation.

elastic modulus；compression modulus；deformation modulus

TU44

A

1000-4866(2010）04-0016-03

郭焱,女,1974年12月出生,1996年7月毕业于西安建筑科技大学（工民建专业）,2004年7月毕业于太原理工大学（土木工程专业）,现在大同煤矿集团设计研究有限责任公司工作,工程师。

曹瑞钠,男，1984年10月出生，沈阳建筑大学土木工程学院（岩土工程专业）硕士研究生。

2010-08-04

2010-08-18