基于序列二次规划算法的射孔水平井孔眼分布优化

刘 冰,徐兴平,李继志,石 强

(1.中国石油大学物理科学与技术学院,山东东营 257061;2.中国石油大学机电工程学院,山东东营 257061)

基于序列二次规划算法的射孔水平井孔眼分布优化

刘 冰1,2,徐兴平2,李继志2,石 强1

(1.中国石油大学物理科学与技术学院,山东东营 257061;2.中国石油大学机电工程学院,山东东营 257061)

基于Landman稳态渗流模型和 Su井筒压降模型,考虑射孔密度对水平井产能的影响,建立以水平井产能为目标函数、孔眼位置分布为优化设计变量的两类产能优化模型。采用序列二次规划算法求解优化模型,并对无限导流和有限导流水平井的射孔密度分布进行优化。结果表明:优化射孔能有效地改善沿井筒入流剖面;射孔水平井存在最佳的射孔密度分布;为得到最大产量,无限导流井的射孔密度呈“U”型分布,有限导流水平井的射孔密度沿跟部到趾部方向逐渐降低,约在井筒长度的 3/4位置处取得最小值;若要使沿井筒入流剖面尽可能均匀,则无限导流井的射孔密度呈“∩”型分布,有限导流井的射孔密度沿跟部到趾部方向逐渐升高,约在井筒长度的 3/4位置处取得最大值,但最大产量略有降低。

水平井;孔眼分布;优化模型;序列二次规划算法

水平井射孔完井是开发油气田提高采收率的一项重要技术。在水平井生产过程中,由于井筒趾部与跟部之间存在压差,导致井筒入流剖面不均匀,使得水平井段各部分对整个生产的贡献差别较大,这种现象在底水油藏中极易造成跟部的锥进,严重影响水平井开发效果。因此,合理地进行射孔完井水平井布孔,控制沿水平井井筒流入剖面,对射孔完井水平井控水稳油尤为重要。国内外研究者对水平井射孔完井参数优化进行了相关研究[1-8],但应用序列二次规划 (sequential quadratic programming,SQP)算法优化水平井射孔参数的研究较少。笔者基于Landman的渗流模型和 Su[9]的井筒内流体流动模型,对油藏渗流和井筒内流体流动进行耦合,建立以射孔位置为设计变量、产量为目标函数的水平井产能优化模型,利用 SQP算法[10]具有全局收敛性同时保持局部超一次收敛性的特点,对所建优化模型进行求解。

1 SQP算法的理论基础

SQP算法的基本思想是:在每个迭代点构造一个二次规划(QP)子问题,以这个子问题的解作为迭代的搜索方向,并沿该方向进行一维搜索,最终逼近约束优化问题的解。

对于水平井产能优化问题,可以描述为以下非线性规划形式:

式中,x∈Rn,目标函数f(x)、等式约束hi(x)和不等式约束gj(x)均为连续、可微函数。该问题的拉格朗日函数为

式中,λi和λj为拉格朗日乘子。

非线性规划问题(1)的求解可转化为求搜索方向 d的一系列二次规划子问题[8]。在第k次迭代点xk,二次规划子问题表示为

形成如下形式的新迭代方程:

其中步长参数αk通过不精确线性搜索过程确定[10]。矩阵 Hk为拉格朗日函数式(2)的 Hessian阵的正定近似,按BFGS算法公式[11]更新为

2 射孔完井水平井产能模型

2.1 油藏稳态渗流模型

考虑无限大均质各向同性油藏中的稳态单相渗流,其无限远处为恒压边界,且不考虑钻井污染和射孔压实损害的影响。射孔完井水平井长为L、管壁粗糙度为ε。N个射孔孔眼均看作长为Lp、半径为rp的小圆柱,rp≪Lp。

稳态渗流情况下,根据势理论和叠加原理,第i个孔眼处的压力等于第i个孔眼自身的入流与其他N-1个孔眼入流所产生的压力和,即

式中,pii为入流量为Qi的第i个孔眼在自身位置处产生的压力响应;pij为入流量为Qj的第j个孔眼在第i个孔眼位置处产生的压力响应;xi和xj分别为第i和第j个孔眼的位置坐标;μ为流体黏度;ko为油藏渗透率。

如果把N个孔眼处的压力和入流量看成N维向量,则式(6)可写为

矩阵A=[aij]完全由孔眼的尺寸和位置分布决定,

如果给定沿井筒的压力分布和孔眼分布,则孔眼的径向流入量为

由式(7),(8)看出,如果水平井定产量生产或给定水平井生产端压力降,可调整射孔位置或流入剖面,得到最小的压力降和最大产量,从而优化水平井产能。

2.2 射孔水平井井筒内流体流动压降模型

由于水平井段完全水平,重力损失为零,因此射孔完井方式下水平井段的压力损失就包括井筒管壁造成的摩擦损失Δpwf、油藏流体经孔眼流入水平井井筒造成的加速损失Δpa和混合压力损失Δpm。若沿水平井井筒第i个孔眼处的压力记为pwi,则

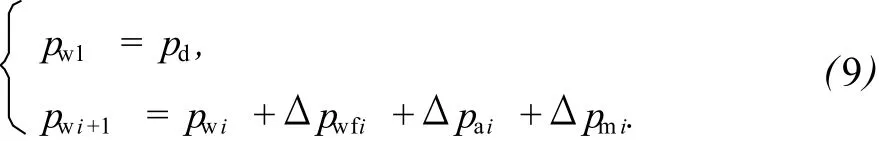
式中,pd为生产端流压。

(1)摩擦损失Δpwf的计算。沿水平井井筒第i个孔眼处的摩擦损失Δpwfi为

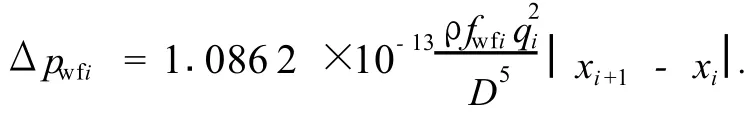
当水平井井筒的流体流动为层流(qi≤qc)时,井筒管壁摩擦系数fwf为

当水平井井筒的流动为紊流(qi＞qc)时,井筒管壁摩擦系数fwf为

式中,qc为水平井井筒内流体流动由层流向紊流转变的临界流量;Re为雷诺数,qi为累积流量;D为井筒直径。

(2)加速损失Δpa的计算。由加速度引起的沿水平井段第i个孔眼处的加速损失Δpai为

(3)混合压力损失Δpm的计算[9]。当水平井井筒的流动为层流(qi≤qc)时,沿水平井井筒第i个孔眼处的混合压力损失pmi为

式中,pp为射孔压力。

当水平井井筒的流动为紊流(qi＞qc)时,沿水平井井筒第i个孔眼处的混合压力损失Δpmi为

沿水平井井筒第i个孔眼射孔后的摩擦系数fpai和射孔前的摩擦系数fpbi间的关系式为

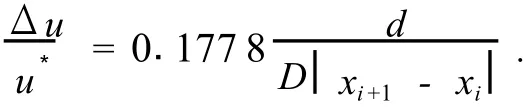
根据射孔水平井井筒内流体流动模型式(9),压力向量可表示为孔眼流入流量向量的函数形式

2.3 油藏渗流和水平井井筒内流体流动耦合模型

根据地层和水平井井筒的耦合条件,水平井井筒与地层处于同一压力系统中,因此该水平井井筒壁面压降应与地层模型中在该处的压降相等,井筒内该处流量应等于其上游孔眼流入流量之和。利用式(6),(8)～(10)对水平井井筒内流体流动和油藏渗流进行耦合,得到油藏渗流-井筒内流体流动耦合的有限导流水平井产能模型,其迭代格式为

给定初值d,i=1,2,…,N,利用式(11)进行迭代得到沿程流压和孔眼流入量,进而得到射孔水平井的产量。

3 孔眼分布优化模型

若给定射孔水平井生产压差,则以水平井产量为目标函数,以孔眼位置分布为优化设计变量,通过优化射孔分布得到水平井最大产量,可形成优化模型 Ⅰ和 Ⅱ。优化模型 Ⅰ可只对孔眼位置分布进行优化设计,减少油藏渗流阻力,使水平井产量最大化。优化模型 Ⅱ可合理地进行射孔完井水平井布孔,调控沿程入流剖面,使其在尽可能均匀的前提下达到产量最大化,从而实现控水稳油提高采收率的目的。

由于射孔数N一般较大,为减少计算量,采取分段数值计算的方法,沿跟部到趾部将水平井划分为J段,每段有I个孔眼(N=JI)分布在下列区间:

经过上述变换,优化模型中设计变量的个数由N个减少到J-1个。

3.1 优化模型 Ⅰ

若不考虑沿程压力损失,则压力向量为一常数,此时水平井为无限导流水平井,其产能优化模型Ⅰ为

考虑沿程压力损失,则有限导流水平井的产能优化模型Ⅰ为

3.2 优化模型 Ⅱ

如果考虑抑制水、气锥进问题,则水平井单位长度上流入量应尽可能均匀。因此,用水平井单位长度的均匀入流量对式(12)和(13)分别加以约束,可得无限导流井和有限导流井的产能优化模型 Ⅱ。

无限导流水平井产能优化模型 Ⅱ为

有限导流水平井产能优化模型 Ⅱ为

式(12)～(15)中,目标函数前加负号转化为负值是为了使产能满足最小值问题。

4 优化模型的 SQP算法求解

4.1 基础参数

胜利油田某井基础参数为:流体黏度μ=55 mPa·s;流体密度ρ=0.904 g/cm3;井筒有效直径D=0.1246 m;井筒粗糙度ε=0.001 m;井筒长度L=137 m;孔眼数目N=400;孔眼半径rp=0.011 m;孔眼长度Lp=0.525 m;油藏平均渗透率ko= 2.868μm2;供给压力pe=18.4MPa;井口压力pd= 0.5 MPa;水平井产量 50 m3/d。计算时水平井井筒分段数J=20,每段射孔数I=20。

4.2 优化模型计算结果分析

利用 SQP算法对优化模型进行求解,得到产量最大时无限导流井和有限导流井射孔密度和入流剖面对比图(图 1,2)。

图1 优化模型Ⅰ的计算结果Fig.1 Calculation results of opt im ization modelⅠ

从图 1可以看出,水平井井筒中的流动是流量逐渐增加的变质量流动,在趾部与跟部存在明显的端部效应。由于水平井趾部和跟部处的供给范围较大,地层流体集中流入水平井井筒,该处的壁面入流量较大。射孔渗流段的相互干扰由趾部和跟部向中部逐渐增强,水平井井筒中部供给范围小,壁面入流量较小。因此,为了得到最大产量,须在水平井跟部生产压差最大的地方多射孔。由于不存在井筒压降,无限导流井壁面入流量对称分布,则射孔密度也是对称的,呈“U”型分布。由于井筒压降的存在,有限导流井的壁面入流量沿水平井跟部到趾部的方向逐渐降低,则射孔密度沿水平井跟部到趾部的方向递减,约在距水平井跟部 3L/4处达到最小,在趾部处又有所增加。

图2 优化模型Ⅱ的计算结果Fig.2 Calculation results of opt im ization modelⅡ

图1说明,若要获得最大产量,需要在生产压差最大的地方多射孔,但如果考虑延缓水、气锥进问题,则应尽量使径向入流均匀。在径向入流均匀的条件约束下,径向入流量较高的地方应减少射孔密度,径向入流量较低的地方应增加射孔密度。如图 2所示,在径向入流量尽可能均匀的约束下,当产量达到最大时,无限导流水平井的射孔密度分布沿水平井中点处对称,呈现“∩”型分布,与其径向入流流量分布相反。由于井筒压降的存在,有限导流水平井跟部压降大,径向流量高。沿井筒跟部到趾部方向径向入流量逐渐降低,在趾部附近又升高。因此,有限导流水平井的射孔密度在跟部相当低,沿井筒方向增加,约在距水平井跟部 3L/4处取得最大值,在趾部处又降低,但对产量的影响不是很大。

表 1为水平井井筒内压降和总产量的计算结果对比。可以看出,无限导流井的优化模型估算的油井产量偏高。由于存在井筒压降,可通过变密度射孔方式优化产能,有限导流水平井最大产量比无限导流井降低约20%。尽管均匀入流剖面能有效地延迟水、气锥进现象,但通过变密度射孔方式获得均匀入流剖面优化产能时,井筒内压降损失最大,最大产量降低。

表1 压降和产量优化结果对比Table 1 Comparison of pressure drawdown and production from different opt im ization models

5 结 论

(1)优化射孔密度分布能有效地改善水平井段的入流剖面。要获得最大产量,无限导流井的射孔密度呈“U”型分布,有限导流水平井的射孔密度由跟部向趾部方向逐渐降低,约在其长度的 3/4处达到最小;要得到均匀的沿井入流剖面,无限导流井的射孔密度为“∩”型分布,而有限导流井的射孔密度则朝趾部方向逐渐升高,约在其长度的 3/4处取得最大值。

(2)受均匀入流剖面的约束,第二类优化模型的产量明显低于第一类优化模型的。

(3)SQP算法可用于水平井射孔分布优化研究。

[1] LANDMANMJ,GOLDTHORPE W H.Optimization of perforation distribution for horizontal wells[R]. SPE 23005,1991.

[2] 周生田,马德泉,刘民.射孔水平井孔眼分布优化研究[J].石油大学学报:自然科学版,2002,26(3):52-54.

ZHOU Sheng-tian,MA De-quan,LIU Min.Optimization of perforation tunnels distribution in perforated horizontal wells[J].Journal of the University of Petroleum,China (Edition ofNatural Science),2002,26(3):52-54.

[3] 周生田.射孔水平井孔眼分布优化分析[J].石油钻探技术,2007,25(5):55-57.

ZHOU Sheng-tian.Opt imization of perforation tunnels distribution in perforated horizontalwells[J].Petroleum Drilling Techniques,2007,25(5):55-57.

[4] MARETTB P,LANDMANMJ.Optimization of perforation distribution for horizontal wells in reservoirs with boundaries[R].SPE 25366,1993.

[5] 汪志明,徐静,王小秋.水平井两相流变密度射孔模型研究 [J].石油大学学报:自然科学版,2005,29 (3):65-69.

WANG Zhi-ming,XU Jing,WANG Xiao-qiu.Study on variable density perforating model of two-phase flow in horizontalwells[J].Journal of the University of Petroleum,China(Edition of Natural Science),2005,29(3): 65-69.

[6] 汪志明,魏建光,王小秋.水平井射孔参数分段组合优化模型 [J].石油勘探与开发,2008,35(6):725-730.

WANG Zhi-ming,WEI Jian-guang,WANG Xiao-qiu. Opt imization modelofperforation parameters for horizontal well[J].Petroleum Exploration and Development,2008, 35(6):725-730.

[7] 王瑞和,张玉哲,步玉环,等.射孔水平井产能分段数值计算 [J].石油勘探与开发,2006,33(5):630-633.

WANG Rui-he,ZHANG Yu-zhe,BU Yu-huan,et al.A segmentally numerical calculation for estimating the productivity of perforated horizontalwells[J].Petroleum Exploration and Development,2006,33(5):630-633.

[8] 王树平,李治平,罗勇.水平井射孔孔眼分布方式优化分析[J].钻采工艺,2007,30(2):39-41.

WANG Shu-ping,LI Zhi-ping,LUO Yong.Analysis of perforation tunnel distribution model in horizontal well [J].Drilling&Production Technology,2007,30(2): 39-41.

[9] SU Z,GUDMUNDSSONJS.Pressure drop in perforated pipes:experiments and analysis[R].SPE 28800,1994.

[10] 王才经.现代应用数学[M].东营:石油大学出版社,2001:9-11.

[11] 黄平,孟永钢.最优化理论与方法[M].北京:清华大学出版社,2009:85-87.

Opt im ization of perforation distribution of perforated horizontal well based on sequential quadratic programm ing algorithm

LIU Bing1,2,XU Xing-ping2,LIJi-zhi2,SH IQiang1

(1.College of Physics Science and Technology in China University of Petroleum,Dongying257061,China;2.College of Electromechanical Engineering in China University of Petroleum,Dongying257061,China)

Based onLandman modelof steady state inflow and Sumodel of pressure drawdown along thewellbore, two typesof optimization modelswere established considering the effectof perforation densityon productivity of horizontalwell,inwhich the production of the horizontalwellwas treated as an objective function and the perforation distribution as a decision-making variable.The sequential quadratic programming algorithm was applied to the optimizationmodelsof horizontalwell established under the conditionsof infinite and finite conductivity respectively.The results indicate that the profilesof inflow rate are improved effectively through optimizing perforation positions and there exists a reasonable perforation density distribution.For a given example,the perforation density distributionwith a shape of“U”leads tomaximum production for the infinite conductive horizontal well.However,the perforation density decreases from the heelof thewellbore to the toe and reaches theminimum at the location of 3/4 length of the well from the heel.Under the constraint of uniform inflow flux,the perforation density distribution shows a shape of“∩”for the infinite conductive horizontalwell.For the finite conductive horizontalwell,the perforation density increases toward the toe of the wellbore and reaches the maximum at the location of 3/4 length of the well.The constraint of uniform inflow flux leads to the decrease in the maximum production of the perforated horizontalwell.

horizontalwells;perforation distribution;optimization model;sequential quadratic programming algorithm

TE 257

A

10.3969/j.issn.1673-5005.2010.04.015

1673-5005(2010)04-0079-05

2010-01-22

国家自然科学基金项目(10805074);山东省自然科学基金项目(Y2008F17)

刘冰(1972-),男(汉族),山东临沭人,副教授,博士研究生,从事计算物理、渗流力学研究。

(编辑 李志芬)