操作风险损失的广义帕累托分布参数估计及其应用

谭德俊,邹敏烨

(湖南大学金融与统计学院,湖南长沙 410079)＊

操作风险损失的广义帕累托分布参数估计及其应用

谭德俊,邹敏烨

(湖南大学金融与统计学院,湖南长沙 410079)＊

极值理论表明大于某一阀值的样本服从广义帕累托分布,该结论在金融风险计量和保险精算中有着广泛的应用。然而,由于其参数没有可接受的估计方法,致使其应用受到限制。论文在推导出广义帕累托分布的条件矩的基础上,研究了基于操作风险损失的广义帕累托分布的参数估计问题。并且基于我国商业银行1994～2008年的操作风险损失数据对经济资本配置进行了算例分析。

极值定理;广义帕累托分布;参数估计;操作风险损失;经济资本

一、引言

极值理论是研究序列极端值分布特征的理论。Fisher和 Tippett(1928)证明了若独立同分布的序列的标准极大值收敛于某分布,则其极限分布就是广义帕累托分布。Gnedenko(1943)证明了序列极端值分布区域应用的极端损失尾部准则。Gumbel (1958)将上述研究成果进行了系统的总结,形成了以第一极值定理为重要结论的极值理论。Pickands,Balkema-De Haan证明了第二极值定理,得到了来自同一总体的简单随机样本,只要选择的临界值u足够大,超过该临界值的样本点近似地服从参数为ξ,μ,σ的广义帕累托分布[1,2]。自Jenkinson (1955)把极值理论应用于风险研究以来[3],极值理论开始逐步在保险和金融领域中广泛应用。Bekiros(2005),Brooks等针对股票市场、期货市场等的研究表明:极值理论方法比其他方法更准确地描述序列分布的尾部特征,是一种比较准确的分位数预测工具,尤其是仅采用较少的样本便能计算出比较准确的VaR值[4,5]。国内不少学者对风险计量以及利用极值理论进行风险计量作了有益的研究。彭建刚等利用有序多分类Logistic模型测量违约概率[6],周好文等对应用极值理论度量金融风险进行了实证研究[7],宋加山等对极值理论中阈值选取进行了研究[8],高洪忠对广义极值理论和它对金融风险的尾部分布进行了研究[9]。

国内外学者的研究都得到了一些有用的结论,然而,实际应用的研究中,由于超过临界值的样本并非所有的样本,尽管它们近似服从广义帕累托分布,但由于很难获得其参数的估计值,这使得极值理论的应用受到了严重的制约。就目前已有的国内外文献看,对形状参数ξ估计的研究取得了比较好的成果,平均余值函数法和Hill估计法是广泛接受的方法。而位置参数μ和尺度参数σ的估计尚未有可以广泛认可的结论,甚至在具体应用中对参数的估计方法是错误的。鉴于极值理论的应用日益广泛,以下试从分析广义帕累托分布的条件矩入手,研究广义帕累托分布的参数估计问题,并基于所搜集的中国商业银行操作风险损失数据,研究防范商业银行操作风险损失所需要配置的经济资本数量。

二、操作风险损失的尾部分布和参数的确定

设 X1,X2,…Xn是操作风险损失样本数据,用u表示阀值,假设超过阀值 u的样本个数为nu,用X1,X2,…Xnu表示超过阀值的样本观测值,设样本X1,X2,…Xnu独立同分布,分布函数为F(x),令:

定义 X相对u的超额值的分布函数为:

显然

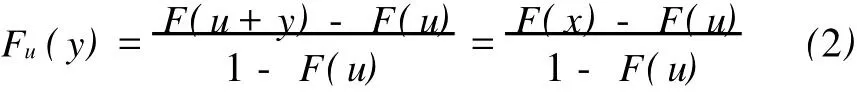
由定理 (Pickands(1975),Balkema-de Haan (1974))得,对充分大的阀值 u,超额值的分布函数近似地服从广义帕累托分布 Fξ,μ,σ(x)。其中:

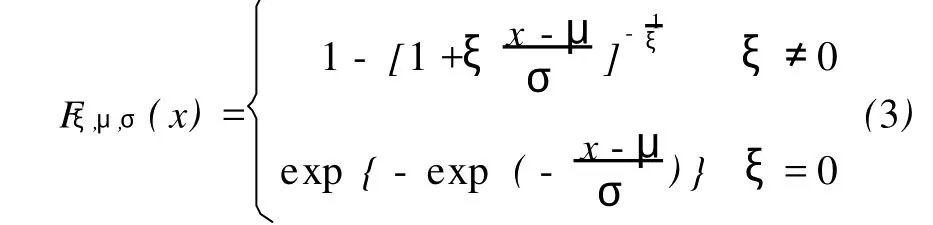
由 F(x)=[1-F(u)]Fu(y)+F(u)得出:

其中,ξ是重要的形状参数,μ是位置参数,而σ是分布的尺度参数。

从理论上讲,阀值应比较大。但阀值越大,用来估计尾部分布函数的样本观察值的数量就越少,估计的参数变化比较大,所以需要找到合适的阀值。在此先研究随机变量 X服从形状参数ξ>0的帕累托分布时的条件期望e(u)=E(X-u|X>u)。

由于 X的分布函数为:

下面考虑样本平均余值函数:

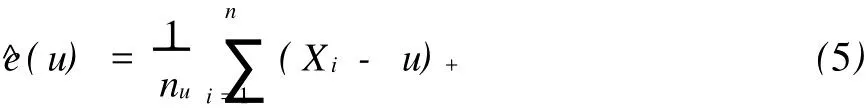
下面来研究操作风险损失的尾部分布的其它参数估计,为此先考虑条件一阶矩 E(X-u|X>u)和条件二阶矩 E[(X-u)2|X>u]。可以证明:

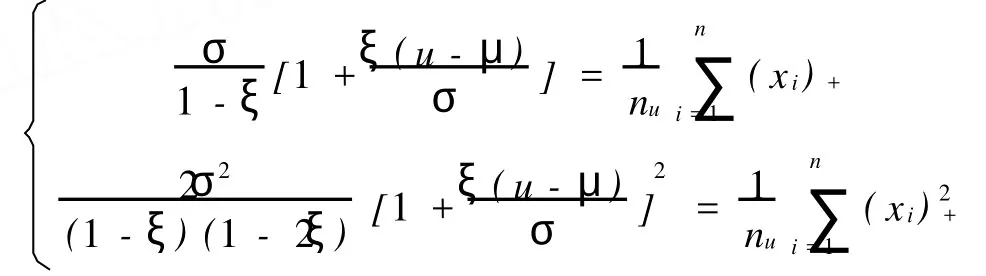
解得:

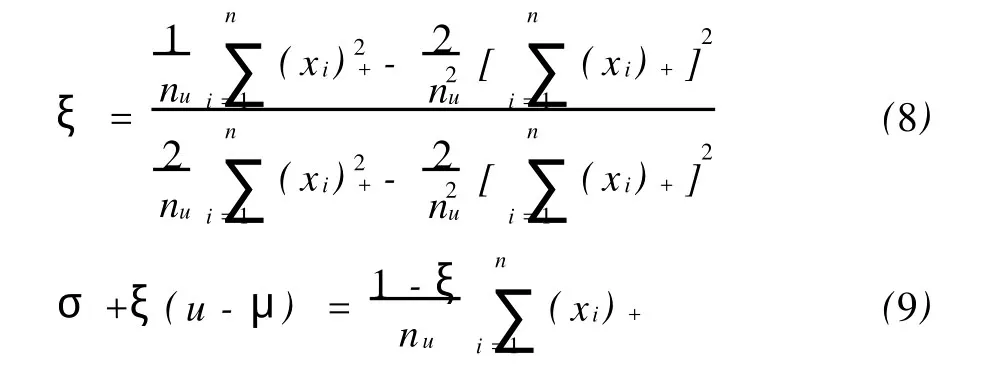
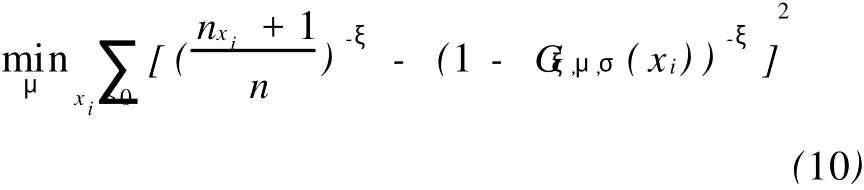
解得:

这样便得到基于条件样本的广义帕累托分布的参数估计值,即操作风险损失超出阀值 u的样本值的极端损失分布函数为:

三、操作风险损失分布及其应用的算例分析

(一)操作风险损失分布的算例分析

算例部分所用的数据来源于中国人民银行银监会网站和国内几大网站的财经新闻专栏及其他相关文献论文中收集到的中国商业银行1994～2008年间的各类操作风险的损失金额数据共计305个。虽然有国有商业银行和股份制商业银行的区别,但是他们的客户群体具有相似性,又处于同样的社会、文化、政治、法律与政策环境下,因此,这些商业银行可视为本质上是同质的,故把它们假设为同一个商业银行的数据,运用其作为案例分析,具有一定的合理性。为研究的方便,假设不同年度以及同一年度各类操作风险损失相互独立并有相同的分布。

根据前面的分析,可以用样本数据得出的平均余值散点图在超过某一特定临界值 u0时基本呈一条直线(或至少具有正斜率)来判定超过临界值 u0的损失值服从广义帕累托分布并据此估计 u0值。平均余值散点图(u,^e(u))见图1。

通过余值散点图(u,^e(u))可以看出,当 u0值取150 000万元左右时,除两点外其余所有的点均呈现明显的正斜率线性变化趋势。因此,选取阀值为150 000万元。从而易得 nu=7,(x299)+=17 920, (x300)+=27 000,(x301)+=50 000,(x302)+= 110 000,(x303)+=120 000,(x304)+=249 400, (x305)+=7 160 640。

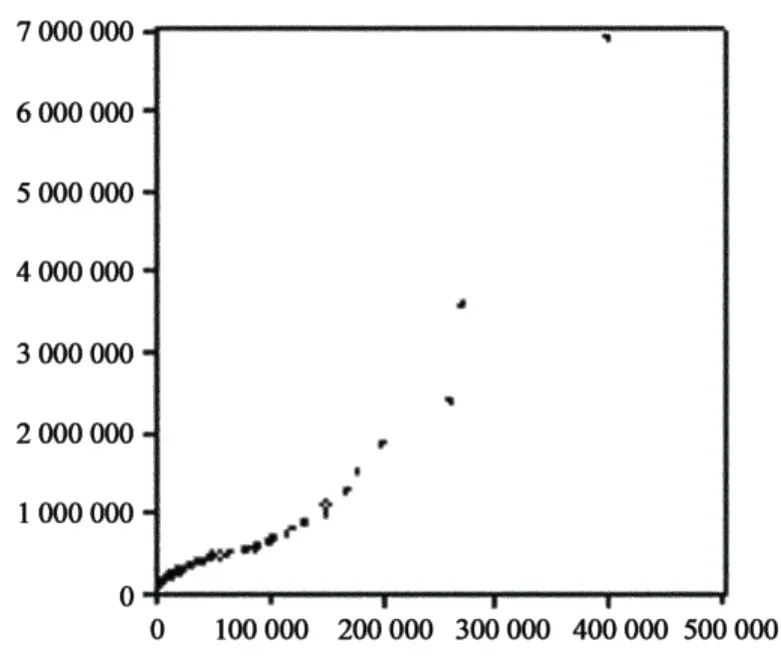
图1 平均余值散点图

将以上样本数据代入式(8)、(11)、(12)就可以得到广义帕累托分布各参数的估计值:^ξ=0.4002, ^μ=-861649.70,^σ=257919.02。将以上参数估计值代入式(13)便得到基于条件样本的广义帕累托分布的参数估计值,即操作风险损失超出阀值 u= 150000的样本值的极端损失分布函数为:

(二)操作风险的经济资本配置

经济资本是指在一定的置信度下,用来吸收或缓冲风险带来的损失的资本。VaR是指在正常的市场环境下,在一定的置信水平和期间内,最大损失的度量。若一定时间内,风险造成的损失为X,则置信水平 p下的VaR值VaRp由P{X VaRp}=p确定。因此,置信度 PF的经济资本便为V aRp,于是,如果风险损失 X的分布函数为 F(x),则VaRp= F-1(p)。

对于给定的置信度 p,VaR值可以由式(14)进行计算得出:

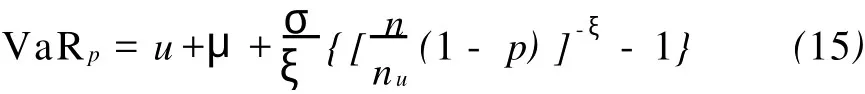
将超出VaRp的极端损失的期望值记为ESp, ESp和VaR的关系如下:

由于ESp是在VaR基础上衍生出来的风险度量方法,与VaR相比,它更能揭示尾部风险的极端情形,更稳定、准确。因此,对操作风险损失事件计算经济资本,选用ESp值比VaR值更为适合。

选取一年作为时间间隔,置信度99.9%来确定经济资本,即取 p=99.9%。根据式(15)即可计算操作风险在99.9%置信度下的最大损失,得:

根据式(16),超过99.9%置信水平的操作风险VaR的期望值为:

于是,在99.9%的置信度下,一年内抵御操作风险需要配置的经济资本约为2 409 102.852万元。

四、结语

极值理论不研究序列的整体分布,只关心序列的极端值分布,不用事先假设样本所来自的总体的分布类型,而是基于同一总体的样本数据本身得到样本极值的变化性质,因此,具有超越总体分布函数类型的估计能力,可广泛应用于信用风险、市场风险、操作风险损失的尾部分布近似,由于其参数没有有效的估计方法,其应用受到了严重的制约。以上在研究广义帕累托分布的条件期望与条件方差的基础上,提出了一种基于条件矩与误差最小相结合的综合估计方法,在利用极值理论分析极端事件损失的概率分布方面有着比较重要的应用,并且通过算例分析为利用广义帕累托分布计量金融风险和配置经济资本提供了一种可行的途径。

[1]Pickands,J..Statistical inference using extreme order statistics[R].Annals of Statistics,1975,3:119-131.

[2]Balkema,A.,and Laurens de Haan.Residual life time at great age[R].Annals of Probability,1974,2:792-804.

[3]Jenkinson A.F.The frequency distribution of the annual maximum(or minimum)values of meteorological elements[J]. Quarterly Journal of the Royal Meteorological Scoiety,1955, (87):158-171.

[4]Stelios Bekiros D,Dimitris Georgoutsos A.Estimation of value at risk by extreme value and conventional methods:a comparative evaluation of their predictive performance[J].International Financial Markets,Institutes and Money,2005,(7):209-228.

[5]Brooks C,Clare A D,Dalle Molle J W,Persand G.A comparison of extreme value teory approaches for determining value at risk[J].Empirical Finance,2005,(3):339-350.

[6]彭建刚,屠海波,何婧,周颖辉.有序多分类logistic模型在违约概率测算中的应用[J].财经理论与实践,2009,(4):2-7.

[7]周好文,杨旭,聂磊.银行操作风险度量的实证分析[J].统计研究,2006,(6):47-51.

[8]宋加山,李勇,彭诚,王彪,方兆本.极值理论中阀值选取的Hill估计方法改进[J].中国科学技术大学学报,2008,38(9):1104-1108.

[9]高洪忠.用POT方法估计损失分布尾部的效应分析[J].数理统计与管理,2004,(7):64-69.

Research on the Parameters Estimation and Application of Generalized Pareto Distribution:Based on Operational Risk Loss

TAN De-Jun,ZOU Min-ye

(College of Finance and Statistics,Hunan University,Changsha,Hunan 410079,China)

Extreme value theory(EV T)shows that the limiting distributions for the maximum of a very large collection of random observations which peak over threshold(POT)and from the same arbitrary distribution are distributed generalized Pareto distribution(GPD).The POT approach has been developed largely in financial risk measurement and actuarial insurance.But its application subjects to the parameters estimation.In this paper,after inferring the condition moments,the parameters estimation of GPD have been researched based on operational risk loss. With the operational risk loss data of Chinese commercial banks from 1994 to 2008,empirical research into economic capital allocation have been carried out.

Extreme Value Theory;Generalized Pareto Distribution;Parameter Estimation; Operational Risk Loss;Economic Capital

F830 文献标识码: A 文章编号:1003-7217(2010)06-0022-04

2010-06-10

教育部博士点基金项目(2006053211);湖南省研究生科研创新项目(CX2009B062)

谭德俊(1964-),男,湖南攸县人,湖南大学金融与统计学院副教授,金融管理与金融工程博士生,研究方向:数理金融与计量金融、数理统计。

(责任编辑:宁晓青)