多特征框架下的蛋白质相似性比较与分类
徐 占, 董洪伟
(江南大学信息工程学院,江苏 无锡 214122)
蛋白质在生物体内占有特殊地位,它是氨基酸通过肽键(peptide bond)互相连接而形成的大分子。由肽键连接氨基酸所组成的化合物称为肽,蛋白质就是一条或多条多肽链聚合而成的分子[1]。它是生物体的基本构件,也是生命活动的重要物质基础,几乎一切生命现象都要通过蛋白质的结构与功能而体现出来。因此,对蛋白质结构和功能的预测成为了当前生命科学中的重要研究内容。众所周知,结构决定功能。所以,蛋白质空间结构的相似性比较就成为了探明蛋白质结构和功能的重要分析手段。而对于两个或多个蛋白质分子而言,其相似性只能大体地说明蛋白质分子之间的相似程度。也就是说,其相似性比较是“模糊”的。这就为运用模糊数学的概念来分析蛋白质空间结构的相似性提供了可能。
此前,很多专家、学者都对蛋白质的空间结构的相似性做了大量的研究[2]。Taylor 等[3]早在1989 年就提出了基于距离矩阵的比较,他们将蛋白质的空间坐标转换成距离矩阵的量化表示,由组成该蛋白质链上的所有骨架原子Cα之间的距离构成一个方阵,然后通过一个相似度计分公式来进行相似性的判定。Holm[4]等在距离矩阵表示的基础上提出了刚性和弹性的相似度函数,通过设定经验阈值获得相似性判定。Choi 等[5]则将距离矩阵划分为许多具有重叠元素的子矩阵,从中抽取有代表性的局部特征的子矩阵集合,利用聚类分析获得K 类局部特征集合,由此将蛋白质结构抽象成K 维欧氏空间的特征点,并求得发生K类局部特征的频率(local feature frequency,LFF)。每一个蛋白质的距离矩阵在进行相似性比较之前先转换成LFF,然后通过计算LFF 之间的距离来获得相似性比较结果。Chi 等[6]则将每一个距离矩阵视为一个纹理图像,利用视觉技术中的图像分割技术定义一系列纹理图像特征值,以刻画蛋白质局部和全部结构特征;并将蛋白质的距离矩阵表示转换成多维图像特征矢量,通过索引技术加快蛋白质结构的相似性查询。浙江大学的胡敏、彭群生[7]提出了一种较为新颖的方法:围绕源结构和目标结构的中心位置进行同心球壳划分,通过计算源结构和目标结构在各划分区域的主要原子的密度来判断两蛋白质分子的相似度。而文献[8-9]都在同一基本原理(即相同立体结构中的各部分只需一个旋转矩阵就能将两者叠合在一起)的基础上对原有的结构比较方法做了进一步地改进。蛋白质的距离矩阵是三维结构的一种二维表示,包含了很多的重构三维结构的信息,但它也有一定的不足,即在很大程度上只是考虑的骨架原子Cα。本文提出一种基于模糊传递闭包理论的结合多特征信息的蛋白质结构相似性比较和分类方法,以提高蛋白质空间结构相似性比较和分类的准确度和效率。
1 理论基础
1.1 模糊等价关系
把论域U 上全体模糊子集所构成的一个集合称为U 的模糊幂集,记为f (U)。模糊等价关系必须满足自反性、对称性和传递性[10]。
定义1设R∈f (U×U),∀u、v、w∈U,若满足:
(1) 自反性 μR(u,u)=1
(2) 对称性 μR(u,v)= μR(v,u)
(3) 传递性 μR(u,w)≥μR(u,v)∧μR(v,w)
则称R 是U 上的一个模糊等价关系。
定义2对于有限论域的情形,U 上的模糊等价关系可表示为一个n×n 的模糊矩阵R=(rij)n×n,并满足:
(1) 自反性 rij=1(主对角线元素全为1),或R⊃I
(2) 对称性 rij=rji(对称矩阵),或R=RT
称此矩阵为模糊等价矩阵。
1.2 传递闭包
人们常常希望利用模糊等价关系(或矩阵)来处理问题,但实际应用中往往获得的是一个具有自反性和对称性的模糊关系(矩阵)——模糊相似关系(矩阵),传递性则较难满足。不过可以对其改造,通过寻找一个包含R 的最小传递矩阵(即传递闭包)来解决问题。
定义3设S,St,R∈Mn×n,t∈T。
(1) 若 ⊇S S oS,则称S 为模糊传递矩阵。
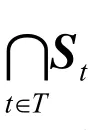
(2) 包含R 的最小模糊传递矩阵叫做R的传递闭包,记作t(R)。它满足:
传递性 t(R)⊇ t(R)ot(R)
包含性 t(R)⊇R
最小性 S⊇R,S⊇SoS⇒S⊇t(R)
下面的问题是如何找t(R)。有
1) 总存在有传递闭包,且
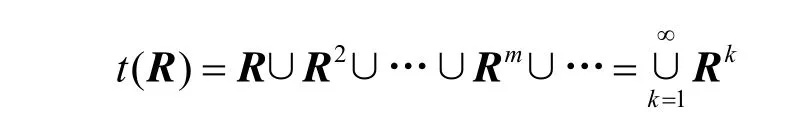
即求传递闭包只需n 次运算。
3) 若R 又是n 阶的模糊相似矩阵,则存在自然数k≤n,使得t(R)=Rk,且对于m>k 时,恒有Rm=Rk。
由此而得的t(R)= Rk是一个模糊等价矩阵。
上面之3)告诉人们:从模糊相似矩阵出发,逐次向后计算
R2, R4, …, R2k
当第一次出现R2k=RkoRk= Rk时(k=1,2,…,n), (1)
实验方法主要参照已发表文献[27]。药物作用足够时间后收集细胞,随后用流式细胞仪进行检测。细胞周期实验用PBS-PI液染色。凋亡实验用PE和7AAD进行染色(按Annexin V/PE凋亡试剂盒说明书进行)。自噬实验用Cyto-ID®进行孵育(按Cyto-ID®自噬检测试剂盒说明书进行)。
此Rk便是传递闭包t(R),即是要寻找的一个包含R 的最小模糊等价矩阵。
2 基于模糊传递闭包的蛋白质结构相似性比较和分类
2.1 基于模糊传递闭包的蛋白质相似性比较与分类
传统的聚类分析是把每个待分类的对象严格地划分到某个类中,体现了非此及彼的性质。因此,这种分类的类别界限是分明的。然而,客观事物之间的界限往往是不分明的,这就提出了模糊划分的概念。自Ruspinis于1969 年提出了模糊划分的概念以来,并在模糊聚类分析方面做出了开创性的工作以后,已经提出了很多基于模糊划分概念的模糊聚类方法,其中传递闭包法就是一种典型的模糊聚类方法。模糊聚类反映了对象属于不同类别的不确定程度,可以更客观地反映现实世界。目前,模糊聚类分析已经广泛地应用于经济学,生物学,气象学,信息科学,工程技术科学等许多领域[11]。传递闭包法聚类首先需要通过标定的模糊相似矩阵R,然后求出包含矩阵R的最小模糊传递矩阵,即R的传递闭包t(R),最后依据t(R)进行聚类。
传统的蛋白质相似性比较多考虑单一特征,且常常是两个蛋白质的相似性比较,而且比较算法复杂,效率不高。本方法基于模糊数学等价矩阵理论,采用多种低维的特征统计量,通过构造蛋白质相性模糊矩阵,运用模糊传递闭包对蛋白质结构相似性进行比较和分类,可以快速地对大量的蛋白质进行相似性标记和分类,可用于快速地对蛋白质进行粗分类和比较,这样就极大地提高了蛋白质相似性比较和分类的效率。
2.2 方法主要过程
基于模糊传递闭包的蛋白质相似性比较与分类方法,首先根据选取的特征参数建立蛋白质组的相似模糊矩阵,然后计算该模糊相似矩阵的传递闭包,最后根据用户指定的置信水平得到蛋白质的分类和相似性结果。具体过程如下:
(1) 确定多特性框架中的蛋白质特征参数,本文中选取骨架原子Cα数、突变原子数、亲水微粒数、螺旋数4 个参数作为刻画蛋白质的特征参数。
1) 骨架原子Cα数
作为蛋白质空间结构的骨架原子—— Cα一直是蛋白质相似性比较的主要研究对象,所以将它作为一个参量。
2) 突变原子数(HETEROGEN ATOMS)
随着基因工程的发展,氨基酸残基的定点突变技术已经广泛地用于蛋白质工程研究中。这一技术在对蛋白分子进行结构与功能的预测和改造中,以及在设计新功能蛋白分子中发挥着不可替代的作用[12]。
3) 亲水微粒数(SOLVENT ATOMS)
相对于亲水微粒数而言,疏水微粒数在蛋白质相似性比较中所起的作用更大,但前者更易获得,故取前者为一个参量。
4) 螺旋数(HELIX)
作为蛋白质二级结构中最主要的结构,将其作为一个参量来进行蛋白质的相似性比较和分类可以极大地提高相似性比较和分类的准确度。
(2) 运用上文中提到的方法建立模糊关系矩阵,然后借助模糊传递闭包求得模糊等价矩阵t(R)。设论域U={Xi|i=1, 2, …, n} 表示待比较的蛋白质集合,其中每个蛋白质向量Xi= (xi1, xi2, xi3, xi4) 表示上述的4 个特征参数,可以构造蛋白质组的特征参数矩阵A = (X1, X2, …, Xn),从该特征参数矩阵A,可用下述的相似度公式构造模糊关系矩阵R = {rij| i, j = 1, 2, …, n }。
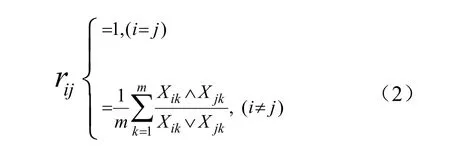

根据公式(1)来计算模糊关系矩阵R 的传递闭包t(R)时,对Xij的取值是这样规定的:对i行j 列的对应元素先进行∧(取小)运算,然后再对所得元素进行∨(取大)运算,直到满足式(1)为止。
(3) 对所得到的不同的λ(置信水平)确定合适的数值,完成对蛋白质的相似性比较和分类。由于所得到的λ(置信水平)在很大程度上取决于构造模糊关系矩阵R 的公式,因此可以根据需要,灵活地选用合适的公式来实现对λ 的获取。一旦确定了λ 的值,就可以返回到t(R)中,对所有的对象进行比较和分类。具体做法为:
1) 将t(R)中所有不同的数值按照从大到小的顺序依次列出,从中选取数值较高的一个λ 值作为对比标准。
2) 找出t(R)中所有大于或等于上述λ 的数值。
3) 对所找到的每一个符合2)条件的数值,找到它所在的行i 和列j,即得到第i 个和第j 个比较对象同属一类,而此处的Rij就作为比较对象的相似度。
4) 将含有交集的分组进行合并,得到最终的分类结果。
3 实验与比较
作者从蛋白质结构数据库PDB 中取ID 号分别为1J4R、102M、2HBF、101M、2HBD、103M的6 个蛋白质分子为研究对象验证上述方法的可行性。
设论域U={X1, X2, X3, X4, X5, X6}表示这6 个蛋白质分子所组成的集合,已知每个蛋白质分子都有4 个参数(骨架原子Cα数、突变原子数( HETEROGEN ATOMS ) 、 亲 水 微 粒 数(SOLVENT ATOMS)、螺旋数(HELIX)),即Xi={ Xi1, Xi2, Xi3, Xi4}。这样就可以得到下面的一个矩阵
利用公式(2)对上述矩阵进行标准化,得到
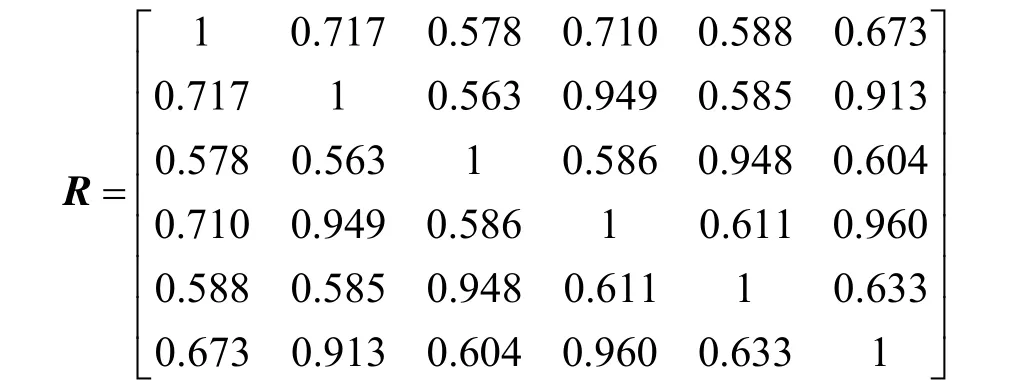
然后,按照公式(1),求得
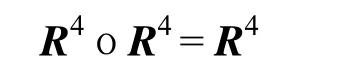
因此,传递闭包为R4,即t(R)= R4。所得结果如下
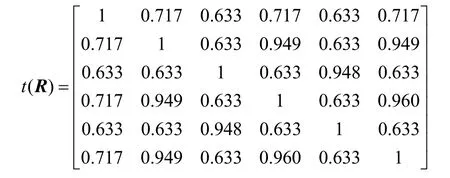
这样,就得到了λ(置信水平)的6 个不同的取值(1、0.960、0.949、0.948、0.717、0.633)。然后依据这6 个数值就可以对上述6 个蛋白质分子进行分类。比如,当取λ(置信水平)=0.948时,分类如下:
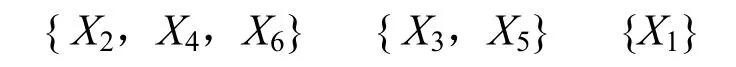
即第2 个、第4 个和第6 个蛋白质分子属于同一类(或者说相似性非常高),第3 个和第5个蛋白质分子属于同一类,第1 个蛋白质分子单独一类。事实上,所选择的6 个蛋白质分子中X2、X4、X6均为肌红蛋白,X3、X5为氧合血红蛋白,X1为一种异构酶。这说明,通过本方法所得到的实验结果与事实是一致的。而且通过与文献[7]方法的比较,如图1、图2 所示,可以得到更高的相似度值。另外,将此方法应用于蛋白质结构的相似性比较,还可以改变4 个参数(数量或内容)来获得更好的实验结果。图3 是运用上述方法计算得到的另外三组蛋白质的比较结果。
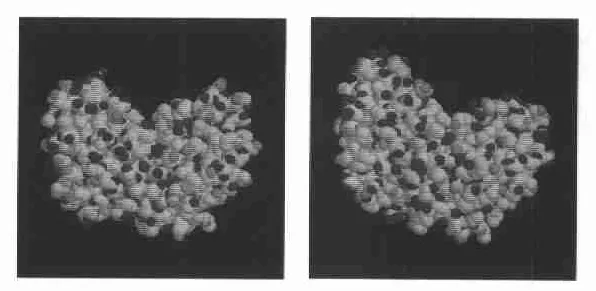
图1 氧合血红蛋白2HBD-2HBF 相似度值
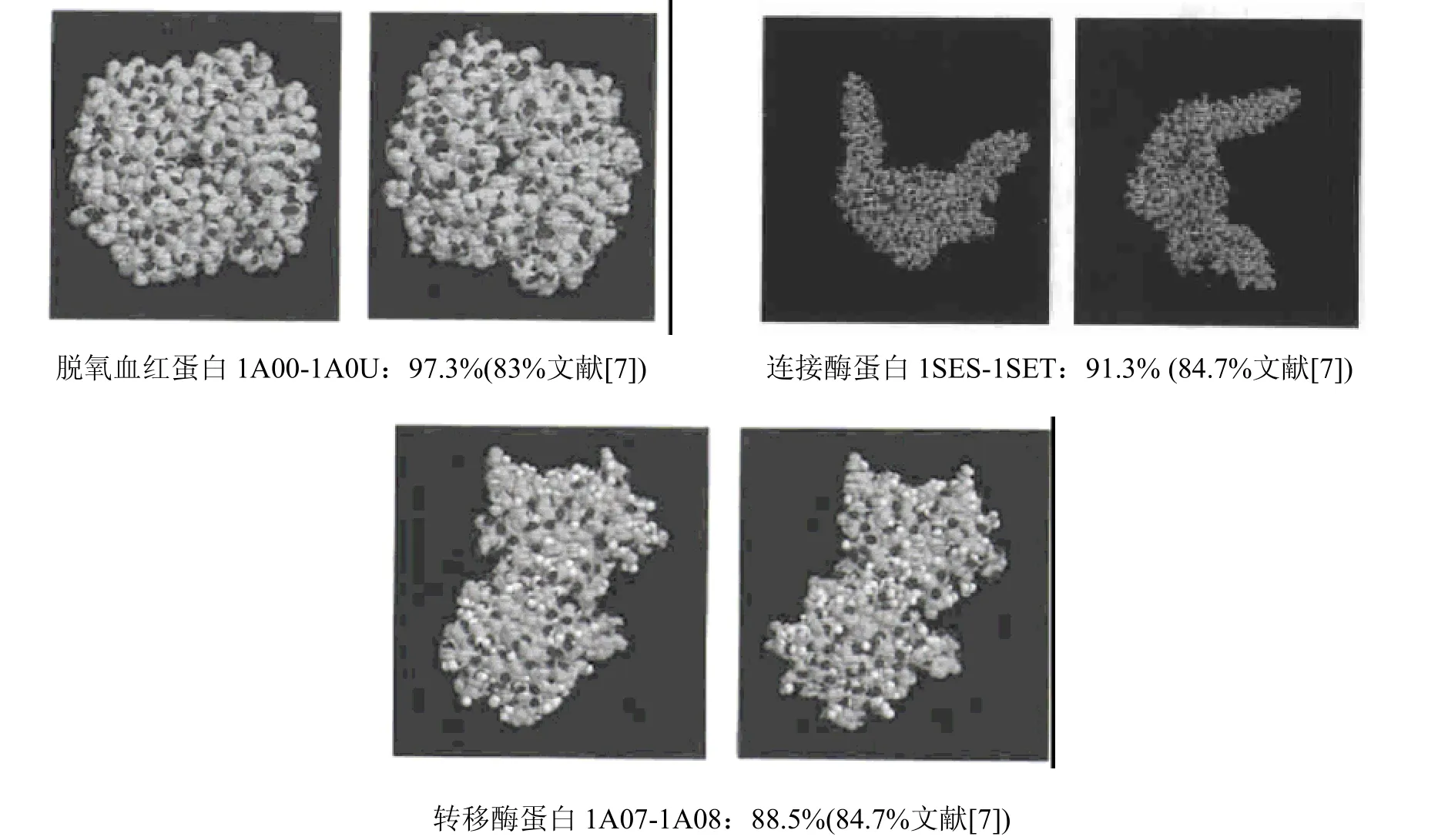
图3 脱氧血红蛋白、连接酶蛋白、转移酶蛋白的比较结果
4 结 论
传统的方法一般利用蛋白质的单一结构表示获取多维特征矢量,通过每种特征的加权平均获得最后的计算结果,在计算过程中常常产生维数很高的特征矢量,使得计算复杂化。与传统的多种属性加权比较的方法不同。本方法采用多种低维的特征统计量,然后运用模糊数学等价矩阵的理论从以下4 个方面:骨架原子Cα数、突变原子数(HETEROGEN ATOMS)、亲水微粒数(SOLVENT ATOMS)、螺旋数(HELIX)等进行综合评判。与基于距离矩阵等其他方法相比,本文所提出的方法具有两大优势:一方面,综合考虑到了蛋白质分子组成的4 个重要方面,而非单纯研究其骨架原子Cα,又加上各种特征之间有一定的相互弥补的作用,这样大大提高了相似性判断的准确度;另一方面,利用该方法不但可以对两个蛋白质分子进行相似性比较,更可以同时比较多个蛋白质分子的相似性,极大地提高了相似性比较的效率。
[1] 陶士珩. 生物信息学[M]. 北京: 科学出版社, 2007. 151-159.
[2] 彭群生, 胡 敏. 蛋白质三维结构相似性比较方法综述[J]. 计算机辅助设计与图形学学报, 2006, (10): 1466-1469.
[3] Taylor Willim R, Orengo Christine A. Protein structure alignment [J]. Journal of Molecular Biology, 1989, 208(1): 1-18.
[4] Holm Liisa, Sander Chris. Protein structure comparison by alignment of distance matrices [J]. Journal of Molecular Biology, 1993, 233(1): 123-138.
[5] Choi In-geol, Kwon Jaimyoung, Kim Sung-hou. Local feature frequency profile: a method to measure structural similarity in protein[C]//Proceedings of the National Academy of Sciences of the United States of America, 2004: 3797-3802.
[6] Chi Pin-hao, Scott Grant, Shyu Chi-ren. A fast protein structure retrieval system using image—— based distance matrices and multidimensional index[C]//Proceedings of IEEE Symposium on Bioinformatics and Bioengineering (BIBE’04), Taichung, 2004: 522-529.
[7] 胡 敏, 彭群生. 一种基于空间密度特征的蛋白质结构相似性判定方法[J]. 工程图学学报, 2005, 26(1): 91-93.
[8] 徐建平, 方慧生, 相秉仁. 一种快速比较蛋白质结构预测模型相似性的方法[J]. 中国药科大学学报, 2006, 37(3): 281-283.
[9] 陈克宾, 黄文奇. 蛋白质三维连续结构模型结构预测的高效算法[J]. 计算机工程与科学, 2007, 29(4): 68-71.
[10] 曹谢东. 模糊信息处理及应用[M]. 北京: 科学出版社, 2003. 30-31.
[11] 罗兰星. 模糊聚类分析中传递闭包法及其应用[J].四川省卫生管理干部学院学报, 2005, 24(2) : 108-109.
[12] 林英武, 黄仲贤. 血红素蛋白的分子设计新趋向[J].化学进展, 2006, 18(6): 795-797.

