怎样在数学教学实践中培养学生的创新能力
陈冬云
[摘要]数学教育作为中学教育中的一门最普通、最基本的学科教育,它在人的素质养成上具有其它学科不可替代的作用。在数学教学中培养学生的创新能力要从多方面入手:(1)鼓励学生参与讨论、发现,激活创造思维。数学教学,本质上是一种数学活动。通过活动,让学生学习自行获取数学知识的方法,学习主动参与数学实践的本领;进而获得终身受益的数学基础能力和创造能力。(2)设置情境,让学生参与猜想,培养直觉思维。这样的思维训练,可使学生今后主动迁移到新知识的学习中去,这对学生走入社会后的工作、研究无疑是大有裨益的。(3)创造时机,激发学生参与数学活动,培养实践创造能力。
[关键词]数学教学 学生 创新能力
数学教育作为中学教育中的一门最普通最基本的学科教育,它在人的素质养成上具有其它学科不可替代的作用,为了体现数学教育在素质教育中的特殊功能,教师应设法使学生在学习过程中极大地体现出创新精神。学生创新能力的培养是多方面的。在课堂教学中应注重从多方面培养学生的创新能力。
一、营造自由和谐的气氛,鼓励学生参与讨论、发现,激活创造思维
数学教学,本质上是一种数学活动。通过活动,让学生学习自行获取数学知识的方法,学习主动参与数学实践的本领;进而获得终身受益的数学基础能力和创造能力,教师要营造自由和谐的气氛,鼓励学生积极思考、大胆质疑、不断产生新设想。
例如,在对“等腰三角形的判定”进行教学设计时,我通过具体问题的解决创设出如下问题情境:
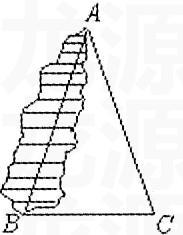
如图,△ABC中,AB=AC,倘若不留神,它的一部分被墨水涂没了,只留下了一条底边BC和一个底角∠C,请问有没有办法把原来的等腰三角形重新画出来?学生先画出残余图形并思索着如何画出被墨水涂没的部分。各种画法出现了:有的学生是先量出∠C的度数,再以BC为一边,B点为顶点作∠B=∠C,与∠C的边相交得顶点A;也有的是取BC中点D,过D点作BC的垂线,与∠C的一边相交得顶点A;也有的是用对折得到。这些画法的正确性要用“判定定理”来判定,而这正是要学的课题。于是我便抓住“所画的三角形一定是等腰三角形吗?”引出课题,再引导学生分析画法的实质,并用几何语言概括出这个实质,即“△ABC中,若∠B=∠C,则AB=AC”。这样,就由学生自己从问题出发获得了判定定理。接着,再引导学生根据上述实际问题的启示思考证明方法。
二、设置情境,学生自觉参与猜想,培养直觉思维
直觉思维又叫猜想,是一种整体的粗线条的跃进式的思维。这种思维在遇到问题时,往往对事物直接感知、整体把握,通过一阵紧张思考,会接触到问题的实质,找到答案。数学中许多性质往往是从特殊到一般,教学中应有意识带着学生归纳总结,使他们养成从特殊现象中发现一般规律的习惯。以下是一课堂案例:
在学习完了平行四边形判定定理之后,如何进一步运用这些定理去判定一个四边形是否为平行四边形?我首先提问学生平行四边形的定义以及四条判定定理,然后分析这五条判定方法的结构:平行四边形的定义和前三条判定定理的条件较单一:相等、或平行,而第四条判定定理是相等与平行二者兼有,如果将它看作是定义和判定(1)中各取条件的一部分的话,那么从定义和前三条判定定理中每两个取其中部分条件是否都能构成平行四边形的判定方法呢?这样我创设了问题情境,根据对第四条判定定理的剖析,使学生用类比的方法提出了猜想:
1.一组对边平行且另一组对边相等的四边形是平行四边形。
2.一组对边平行且一组对角相等的四边形是平行四边形。
3.一组对边平行且对角线交点平分某一条对角线的四边形是平行四边形。
4.一组对边相等且对角线交点平分某一条对角线的四边形是平行四边形。
5.一组对边相等且一组对角相等的四边形是平行四边形。
6.一组对角相等且连结两顶点的对角线平分另一对角线的四边形是平行四边形。
7.一组对角相等且连结两顶点的对角线被另一对角线平分的四边形是平行四边形。
在启发学生得出上面的若干猜想之后,我又进一步强调证明的重要性,以使学生形成严谨的思维习惯,达到提高学生逻辑思维能力的目的,要求学生用所学的5种判定方法去一一验证这七条猜想结论的正确性。经过全体师生一齐分析验证,最终得出结论:七条猜想中有四条猜想是错误的,另外三个正确,猜想中的一个尚待给予证明。学生在老师的层层设问下,参与了问题探究的全过程。不仅对知识理解更透彻,掌握更牢固,而且从中受到观察、猜想、分析与转换等思维方法的启迪, 思维品质获得了培养,同时学生也从探索的成功中感到喜悦,使学习数学的兴趣得到了强化,知识得到了进一步发展。通过对教材的独特处理,把学生的学习过程设计成一个模拟性的“科研”活动。这样的思维训练,可使学生今后主动迁移到新知识的学习中去,这对学生走入社会后的工作、研究无疑是大有裨益的。
三、创造时机,激发学生参与数学活动,培养实践创造能力
在教学活动中,我注意提供各种机会让学生参与活动,亲手操作实践 。教育家陶行知说过:“人生两个宝,双手和大脑。”动手、动脑是培养学生创新能力,促使他们通过操作形成表象、直接感知和体验,从而发展学生的形象思维,通过创设问题情境,激活学生的“最近发展区”,启动学生思维,学生更加乐意投入到新的学习情境中去了。例如教“三角形内角和定理”就可以通过实践操作的办法来创设教学情境。学生的认知结构中,已经有了角、三角形的概念,还具有了有关平行线的性质。这些都是学习新知识的“联系点”,但大部分同学都难以想到对三角形内角之和进行研究,这种情况下,我创设这样的问题情境:
在回顾三角形概念的基础上,提出:“三角形的三个内角会不会存在某种关系呢?”这是纲领性提问,对学生的思维还达不到确定的导向作用,我适时地提出:“三个内角的和是否有一定的规律?”他们的思维可能会指向“三个内角的和是否有一定的规律?”接着“请同学们画一个三角形,再用量角器量出三个角,观察一下三角形的三个内角有什么联系?”经测量、计算,学生发现三个内角的和在180°左右。我再进一步提出:“由于具体测量会有误差,但和数都在180°左右,三角形的三个内角之和是否为180°呢?请同学们把三个角拼在一起,看一看,构成了一个怎样的角?”学生在完成这一实验后发现,三个内角拼在一起构成一个平角。经过上述两步实验,提出“三角形的三个内角之和为180°”的猜想就水到渠成了。接着,我指出了实验操作的局限性,并要求学生给出严格的逻辑证明。在寻找证明方法时,我提出:“观察拼接图形,从中能得到什么启示?”学生可凭借实践操作时的感性经验,找到证明方法。实践操作不但使学生获得了定理的猜想,而且受到了证明定理的启发,显示了很大的智力价值。
教育的核心是创造教育,教师在教育教学过程中应不断激发和培养学生获取知识的能力,让学生以主人翁态度参与学习,通过动口、动手动脑等多种形式培养学生自身实践能力和创造才能。

