对勾股定理一种推广方式的探究

李俊永

勾股定理有着各种不同形式的推广,其推广所用的方式也是不同的,本文所介绍的一种推广是用所谓联系拓广的方式,它是探索新的教学命题的一种重要方法.

我们知道,在直角△ABC中,设∠C=90°,则有结论:AB²=AC²+BC².这就是大家熟悉的勾股定理,如果我们将它和圆联系起来考虑,就可以把这一定理推广.

一、问题的提出

作直角△ABC的外接圆,如图1所示,再延长两直角边AC、BC,如图2所示,这时直角△ABC可看作是过圆一直径的两端点A、B作两直线,当其交点C在圆周上时所形成的图形.用这种观点来看,过直径两端所作的两相交直线其交点在圆周上,这仅是一种特殊位置,交点还可以在圆内,也可以在圆外.因此,从圆与过圆直径两端点所作的两相交直线的关系来看,可将勾股定理加以推广.

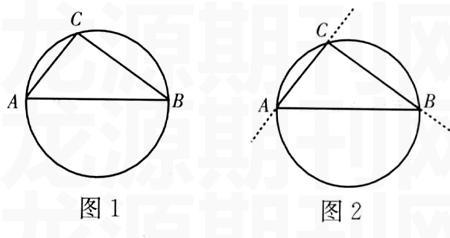
二、问题的猜想

在图2的基础上,如果以A为固定点,将AC顺时针旋转一个角度,这时两直线AD、BC在圆内相交于E,如图3所示,当AC旋转时,AE•AD比AC²越来越大,而BE•BC比BC²越来越小,这时AE•AD+BE•BC可猜想为常量AB²,即AE•AD+AC•BC=AB².①

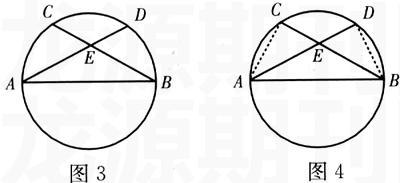
三、问题的解决

之所以这样猜想,是因为通过以上分析我们知道,当AC处于两种特殊位置时,一种是图2所示的位置,一种是当AC旋转到与AB重合时,①式都是成立的.

下面证明对于一般情况①式也是成立的.

连结AC、BD,如图4所示,于是有

AB²=AC²+BC²,

AB²=BD²+AD²,

而AC²=AE²-EC²=AE²-(BC-BE)²,

BD²=BE²-ED²=BE²-(AD-AE)²,

所以2AB²=AE²-(BC-BE)²+BC²+BE²-(AD-AE)²+AD²=2(AE•AD+BE•BC).

故①式得证.

四、问题的推广

通过以上讨论,我们对勾股定理可作如下推广:

定理1 从圆的直径AB的两端引两弦AD、BC,在圆内交于E,则有

AB²=AE•AD+BE•BC.

在图3中,如果AD逆时针方向旋转,①式右端第一项逐渐减小,第二项逐渐增大,当其交点在圆外相交于E时(如图5所示),第二项BE•BC继续增大,第一项AE•AD逐渐减小,我们可以继续旋转到当AD=0时,也就是说AE与圆相切于A时(如图6所示),这时①式变成AB²=BE•BC,这是大家所熟知的射影定理.由此可猜想如图5所示的位置,①式也成立.其证明与上面类似.

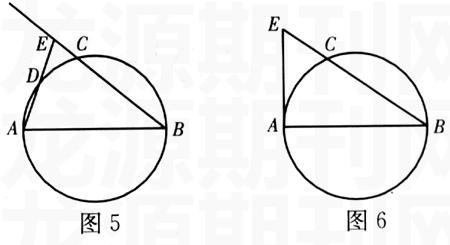
定理2 以△EBA的AB边为直径作圆,分别交AE、BE边于D、C,则有AB²=AE•AD+BE•BC.

在图6中,当AE继续逆时针方向旋转时,这时BE•BC就要大于AB²,连结AC、BD,如图7,AB²=AC²+BC²,AB²=BD²+AD²,

而AC²=AE²-EC²=AE²-(BE-BC)²,

BD²=BE²-ED²=BE²-(AE+AD)²,

所以2AB²=AC²+BC²+BD²+AD²=AE²-(BE-BC)²+BC²+BE²-(AE+AD)²+AD²=2(BE•BC-2AE•AD).

故AB²=-AE•AD+BE•BC.②(如图7所示)

对称地,如图8所示有AB²=AE•AD-BE•BC.③

参考文献:

[1]吕峰.一堂开放式探究习题课[J].中学数学教学参考,2005,(7).

[2]程新林.一道几何题的联想[J].中学教研,1989,(2).

[3]严士健等.普通高中数学课程标准(实验)解读[J].南京:江苏教育出版社.2004.

(责任编辑:金 铃)