盾构隧道错缝拼装衬砌计算模型研究

杨 钊，潘晓明 同济大学地下建筑与工程系，上海 230092 岩土及地下工程教育部重点实验室(同济大学)，上海 200092

王丽欣 (沙市大学土木工程系，湖北 荆州 434000)

盾构隧道错缝拼装衬砌计算模型研究

杨 钊，潘晓明 同济大学地下建筑与工程系，上海 230092 岩土及地下工程教育部重点实验室(同济大学)，上海 200092

王丽欣 (沙市大学土木工程系，湖北 荆州 434000)

针对盾构隧道错缝拼装的特点，提出了一种新型的错缝拼装环间接头模型，并给出了模型中参数的确定方法与取值范围。利用该模型建立了盾构隧道错缝拼装管片结构受力分析的拟三维仿真模型，分析了上海某过江输水隧洞的通水运营工况，结果表明，错缝拼装衬砌比通缝拼装结构的相对变位要小，结构内力值要大，环间接头模型可以较好地反映错缝拼装在隧道三维工作状态中的约束作用。

错缝拼装；螺栓；剪切弹簧；双线性剪切模型

通缝拼装是一种柔性设计理念。在通缝拼装方式下衬砌结构获得较好的柔性，在良好地层中采用这种拼装方式，能够充分调动周围土层的抗力，在保证衬砌结构满足使用要求的前提下使衬砌设计更加经济合理。相对于通缝拼装，错缝拼装能使圆环接缝刚度分布均匀，减小接缝以及管片环的变形。因此在防水要求较高的盾构法隧道(如过江，海底隧道)或软土地区盾构隧道中，往往采用错缝拼装的方式，以取得较好的空间刚度，达到长期防水的目的[1～3]。错缝设计的难点在于采用何种计算模型来计算环与环之间的剪力传递(即环与环之间的相互约束)。这种相互约束主要体现在环面之间的摩擦、纵向螺栓的抗剪以及榫头与榫槽的咬合等。国内外众多学者针对环间接头提出了多种模型。文献[4]的计算模型中，忽略环面的摩擦作用以及螺栓与螺栓孔之间的空隙，假定环间接头处没有相对位移，即认为环间传递剪力的剪切刚度为无穷大，但在实际工程中螺栓与螺栓孔之间存在间隙，环间的相对位移存在。文献[5]在环向接头处设置径向剪切弹簧与切向剪切弹簧来模拟纵向接头的有限刚度，并给出了弹簧刚度的理论计算公式，这种模型忽略了环面与环面之间摩擦力对剪力传递的贡献，其理论计算公式中一些参数缺少理论依据且难以确定，实际设计中应用不方便。笔者在综合考虑环面之间摩擦与纵向螺栓抗剪的基础上，提出了一种新型的环间接头模型——双线性剪切弹簧模型，并基于理论推导给出了双线性剪切弹簧模型的刚度系数。

1 环间接头模型——双线性剪切弹簧模型的建立

图1 环向接头抗剪刚度

当纵向螺栓与螺栓孔之间不发生接触时，环间剪力由相邻环面之间的摩擦力来传递，摩擦力的方向与相邻环面相对位移方向相反。因环间摩擦力相对较小，因此可以假定剪力作为集中力作用在纵向螺栓处，剪力的方向与环向接头之间相对位移方向相反。当纵向螺栓与螺栓孔之间发生接触时，环间剪力主要通过纵向螺栓的抗剪来传递，即剪力以集中力形式施于纵向螺栓处，剪力的方向与环向接头之间相对位移方向相反。因此可以在纵向螺栓处设置剪切弹簧用于模拟错缝拼装衬砌的环间剪力传递，其中剪力的方向与环向接头之间相对位移方向相反。

根据上面分析，剪切弹簧的刚度分为2个阶段(见图1)：第1阶段，纵向螺栓与螺栓孔之间未发生接触，弹簧的抗剪能力主要取决于环间的摩擦力，弹簧的刚度系数取为K1；第2阶段，纵向螺栓与螺栓孔相接触，弹簧的抗剪能力主要取决于螺栓的抗剪能力，弹簧的刚度系数取为K2。

1.1第1阶段弹簧剪切刚度

假定盾构衬砌的内半径为r，外半径为R，一个衬砌环有n根纵向螺栓，每根纵向螺栓的预紧力为T，螺栓与螺栓孔之间的间距为d(理想状态为螺栓孔的直径减螺栓杆的直径)，环与环面之间的摩擦系数为μ。则第1阶段剪切刚度K1可按下式计算：

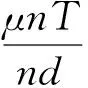
(1)

1.2第2阶段弹簧剪切刚度

第2阶段弹簧的剪切刚度即为螺栓的抗剪刚度。螺栓剪切刚度是一个综合量，它是螺栓的剪切变形、拉伸变形和孔壁挤压变形等因素的综合结果。到目前为止，尚未有文献给出严格的螺栓剪切刚度理论计算公式。螺栓的剪切刚度研究主要采用试验与数值模拟的方法[6～10]，根据大量的试验数据与数值模拟结果，螺栓的抗剪刚度量级应取为107N/m。

2 拟三维有限元模型的建立

2.1模型基本假定

隧道衬砌结构沿隧道纵向可以认为是一个无限长的结构体，在不考虑纵向变形的条件下，且假定环与环之间只传递剪力作用，则剪力的作用施加在管片上，只会引起平面内内力的变化，而不会引起空间内内力的变化。管片环的内力不沿纵向发生变化，因此在计算过程中，可以将每一环管片作为一个平面应变状况考虑。在计算错缝拼装时，取2个平面应变的错缝拼装环计算即可。此方法即为用平面应变问题替代计算空间问题的简化计算方法。

2.2土体结构的有限元模拟

笔者采用ABAQUS程序中的二维4节点等参单元模拟土体结构。考虑到土体材料的弹塑性，选用Drucker-Prager屈服准则和相关联流动法则来模拟土体材料的非线性应力-应变特性[11]。工程实践与理论研究表明：当隧道上覆土层为砂性土时，采用水土分算[12,13]，水压力直接作用于管片上，土体的容重采用浮容重计算，土体的侧压力系数取k0。

2.3管片结构有限元仿真

探讨衬砌管片在错缝拼装方式下的受力特征及规律，由于不需要考虑管片的强度及破坏问题，因此可将管片用线性梁单元来模拟。纵向接头对管片受力的影响，通过在接头处设置抗弯、抗压、抗剪3根弹簧来实现。环向接头对管片受力的影响通过在环向螺栓位置处布设剪切弹簧来模拟，剪切弹簧的抗剪刚度模型采用笔者提出的双线性剪切弹簧模型。

2.4管片与土体之间的接触模型

地层与管片之间采用无厚度的Goodman接触单元模拟。接触面的径向力学行为采用“硬接触”模拟，即接触面之间可以传递无穷大的径向压应力，但不能传递径向拉应力(在径向拉力的作用下接触面脱开)。接触面的切向力学行为采用库仑摩擦模拟。库仑摩擦模型用于判断接触面是否发生相对滑移，同时也用于分析相对滑移对管片衬砌应力场的影响。

库仑摩擦模型可以定义如下：

|τtrue|≤τmax=μP

(2)

式中，τtrue为计算所得的真实剪应力；τmax为最大允许剪应力；μ为摩擦系数；P为接触面法向压力。

接触面之间传递的剪应力不能大于接触压力乘以库仑摩擦系数。当迭代计算出的剪应力值大于接触压力乘以库仑摩擦系数时，判定接触面之间产生相对的剪切滑移进入下一步迭代计算。

3 工程实例

图2 有限元计算模型图

上海市某越江输水隧道衬砌外径6.8m，内径6.0m；采用管片的厚度为400mm，宽度为1500mm；每环由一块插入块F，2块邻接块L1、L2和3块标准块B拼装而成；采用2环1循环的错缝拼装方式，2环之间相互错开180°。纵缝接头采用2根M39的直螺栓连接，为平面接头。环缝采用16根M30的直螺栓连接，螺栓沿圆周方向均匀布置。

有限元计算范围为盾构隧道左右各取30m，地表往下取60m。假设边界左右两侧存在水平约束，下部存在竖向约束，上部边界自由。有限元计算模型图如图2所示。

纵向接头的正、负抗弯、抗压、抗剪刚度系数分别取为：kθ+=4.0×107N/m·rad，kθ-=4.0×107N/m·rad，Kn=5.0×1012N/m，KT=5.0×1011N/m。纵向螺栓的预紧力为100kN，螺栓与螺栓孔之间的间距为8mm，环面与环面之间的摩擦系数为0.3。环向接头的抗剪刚度系数：第1阶段取为0.375×107N/m，第2阶段取为3.0×107N/m。

管片的弹性参数为：

E=3.55×104MPaμ=0.167

其中，E表示弹性模量；μ表示泊松比。

隧道中心处外水压：0.351MPa；隧道内水压：0.31MPa。

土层参数见表1。

表1 土层参数表

4 计算结果分析

在错缝拼装设计的计算中，由于2环的荷载与几何结构均关于竖向轴对称，因此计算所得的管片内力与变位均关于竖向轴对称。

从图3可知，考虑错缝拼装效应与不考虑错缝拼装效应(即通缝拼装)的2种模型所得的管片变位规律相似。管片最大变位位置相同。错缝拼装方式下管片最大水平相对变位为19.2mm，小于通缝拼装方式下的最大水平相对变位(21.7mm)。

从图4可知，2种计算模型所得的管片变位规律相似。管片最大变位位置相同。错缝拼装方式下管片最大竖向相对变位为22.8mm，小于通缝拼装方式下的最大竖向相对变位(25.6mm)。

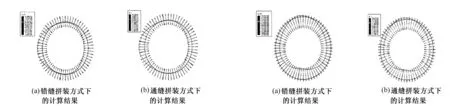
图3 不同拼装方式下管片水平变位图 图4 不同拼装方式下管片竖向变位图

从图5可知，通过2种计算模型所得的管片截面弯矩图变化规律相似。管片截面最大正、负弯矩位置相同。错缝拼装方式下管片最大正、负弯矩分别为233.2kN·m、-245.4kN·m，大于通缝拼装方式下的最大正、负弯矩(分别为230.0kN·m、-187.0kN·m)。

从图6可知，通过2种计算模型所得的管片截面轴力图变化规律相似。管片截面最大轴力位置相同。错缝拼装方式下最大轴力为313.0kN，大于通缝拼装方式下的最大轴力(310.5kN)。在管片两腰处的环与环之间的相互约束主要表现为径向约束，传递的主要为径向剪力，不同拼装方式下最大轴力值变化不大。

图5 不同拼装方式下管片截面弯矩图 图6 不同拼装方式下管片截面轴力图

5 结 论

1)错缝拼装方式下，管片变形受到相邻环的约束作用，管片整体空间刚度增大。管片最大变位值与接头张开量减小，最大内力值增大。

2) 环与环间管片两腰处相对变形最大。其原因主要是由于水平方向的变形不协调，而管片两腰处的竖向方向的变形不协调可以忽略。因而环与环之间传递的剪力值在管片两腰位置处，其竖向分量大而水平向分量小(可以不计)，在管片两腰位置处的轴压值变化较小，而负弯矩最大值变化则较大。

3) 采用笔者提出的错缝拼装环间剪切模型计算所得的管片变位、截面内力均与实际测相吻合。

4)笔者提出的错缝拼装拟三维计算模型建模简单、计算代价小并能反映出错缝拼装衬砌结构受力特征，可以广泛应用于工程实例设计。

[1]刘建航，候学渊.盾构法隧道[M].北京：中国铁道出版社，1991.

[2] 黄钟晖.盾构法隧道错缝拼装衬砌受力机理的研究[D].上海：同济大学，2001.

[3] Blom C B M, Van der Horst E J, Jovanovic P S. Three-dimensional Sturctural Analyses of the Shield-Driven “Green Heart” Tunnel of the High-Speed Line South[J]. Tunnelling and Uderground Space Tchnology, 1999，14(2)：217～224.

[4] 日本隧道协会.日本隧道标准规范(盾构篇)及解释[M].刘铁雄 译.成都：西南交通大学出版社，1993.

[5] 黄钟晖，廖少明，候学渊.错缝拼装衬砌纵向螺栓剪切模型的研究[J].岩石力学与工程学报，2004，23(6)：952～958.

[6] 徐建设，陈以一，韩琳，等.普通螺栓和承压型高强螺栓抗剪连接滑移过程[J].同济大学学报，2003，31(5)：510～514.

[7] 徐建新，王殿春，魏志毅.螺栓配合间隙对剪切刚度的影响[J].机械科学与技术，2000，19(4)：556～558.

[8] 徐建新，夏道家.螺栓剪切刚度可靠性实验研究[J].实验力学，1999，14(4)：533～538.

[9] 张永杰，孙秦.带预应力受剪螺栓刚度研究[J].强度与环境，2007，34(4)：22～25.

[10] 科洛瓦洛夫.剪切螺栓或铆钉连接件的被连接元件孔区内的应力集中[J].朱燕贞 译.紧固与技术，2002，93(1)：22～26.

[11]王仁，黄文彬，黄筑平.塑性力学引论[M].北京：北京大学出版社，2003.

[12] 钟登华，佟大威，王帅，等.深埋TBM施工输水隧洞结构的三维仿真分析[J].岩土力学，2008，29(3)：609～613.

[13] 朱合华，丁文其，李晓军.盾构隧道施工力学性态模拟及工程应用[J].土木工程学报，2000，33(3)：98～103.

[编辑] 李启栋

U451

A

1673-1409(2009)02-N100-04

2009-03-23

杨钊(1984-)，男，2004年大学毕业，博士生，现主要从事盾构隧道仿真与施工方面的研究工作。