线性回归模型系数有偏估计研究

杨 斌 (海军工程大学管理工程系，湖北 武汉 430033)

张建军,瞿 勇 (海军工程大学理学院，湖北 武汉 430033)

线性回归模型系数有偏估计研究

杨 斌 (海军工程大学管理工程系，湖北 武汉 430033)

张建军,瞿 勇 (海军工程大学理学院，湖北 武汉 430033)

针对引起线性回归模型LS估计性能变坏的根本原因，提出了回归系数的广义c-K估计，将众多经典的有偏估计结合在一起，对有偏估计的改进进行了研究，分别证明了最小化均方误差和数量化矩阵K均可对Stein估计进行改进，给出了参数的最优值，为病态线性回归模型系数有偏估计的改进提供了有效途径。

有偏估计；广义c-K估计；岭估计；Stein估计；均方误差；可容许性

考虑线性回归模型:

Y=Xβ+eE(e)=0 Cov(e)=σ2I

(1)

的系数估计问题，其中，I为n×n单位矩阵；Y为n×1观测向量;e为n×1 随机误差向量；X为n×p的设计矩阵，且已中心标准化，且R(X)=p；β为p×1未知参数向量，称为回归系数。

对于p阶的正定方阵S=XTX，必存在正交矩阵Q，使:

QTXTXQ=A

其中，A=diag(λ1,λ2,…,λp),λ1≥λ2≥…≥λpgt;0为S的特征值。假定σ2gt;0，并记Z=XQ，且α=QTβ，则模型(1)可改写为:

Y=Zα+eE(e)=0 Cov(e)=σ2I

(2)

则α的LS估计(Least Squares Estimate，最小二乘估计)为:

针对引起LS估计性能变坏的根本原因，笔者提出了一种新的有偏估计类，研究了有偏估计的改进。

1 广义c-K估计及其基本性质

定义1对模型(2)，定义α的广义c-K估计为:

相应地，定义模型(1)的系数β的广义c-K估计为:

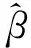
其中，K=diag(k1,k2,…,kp),k1,k2,…，kp≥0称为广义岭参数；参数c≥1称为压缩因子。

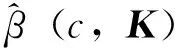
广义c-K估计具有如下性质：

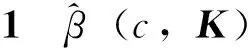
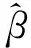
证明只证明性质3，性质1，2可从性质3的证明中得出。

事实上：

再由Q的正交性，得：

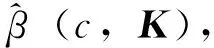
2 对Stein估计的改进

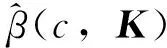
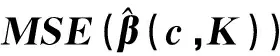
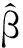
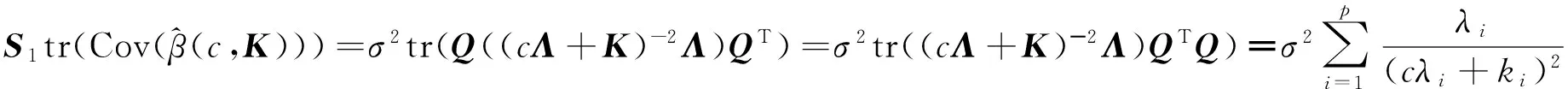
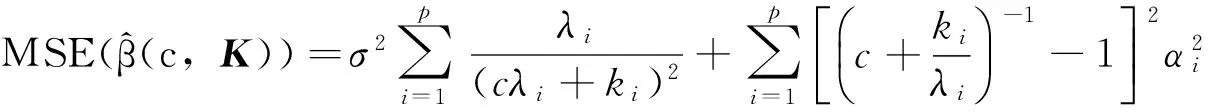
(3)

对该函数最小化，可得以下结果。

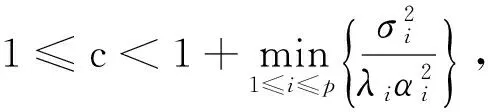
证明由式(3)，有:

将上式分别对k1,k2,…,kp求偏导数，并令其为零，得:

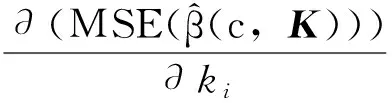
(4)

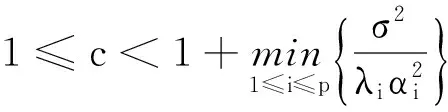
(5)

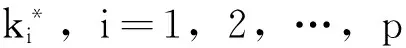
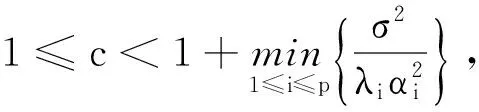
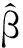
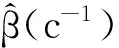
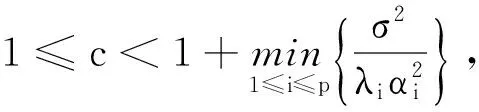
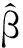
2.2数量化矩阵K以改进Stein估计

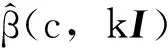
(6)

与式(4)不同，由式(6)直接解出的最优值非常困难，但是，可以研究最优值k*的存在性及其范围。

从而，有下面的结果。

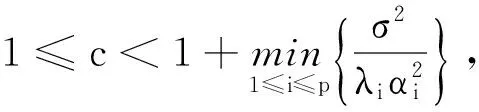
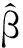
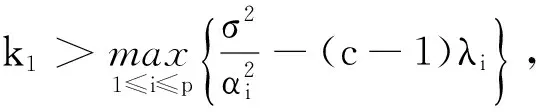
由定理3，还可得到以下结论。

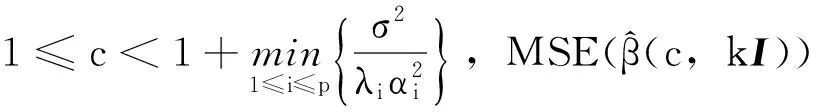
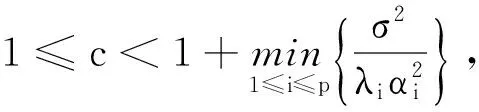
特别重要的是，由上述推论2，再结合文献[9]中的结果，可得以下结论。

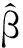
2.3广义c-K估计的偏差

定理6对任意cgt;1及kgt;0，有：

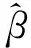
3 广义c-K估计的可容许性

关于可容许性，有如下充要条件:

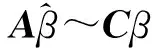
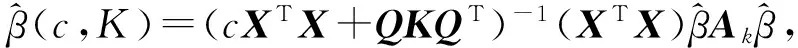
(cXTX+QKQT)-1(XTX)(XTX)-1(XTX)(cXTX+QKQT)-1≤(cXTX+QKQT)-1(XTX)(XTX)-1I

⟺(cXTX+QKQT)-1((c-1)XTX+QKQT)(cXTX+QKQT)-1≥O

(7)

注意到c≥1且K≥O，可知(c-1)XTX+QKQT≥O，从而存在矩阵B，使(c-1)XTX+QKQT=BTB，因而有：

(cXXT+QKQT)-1BT(cXTX+QKQT)-1B≥O

4 结 论

针对引起LS估计性能变坏的根本原因，首次提出了广义c-K估计类，研究了有偏估计的改进问题，分别给出一种最小化广义c-K估计的均方误差和选择数量矩阵K以改进Stein估计的方法，给出了参数的最优值。笔者提出的方法处理工程应用问题中的病态经济模型时，能使某些现象得到更合理的解释。具体的例子，可以参见文献[2]中关于特殊的广义c-K估计的实例。

[1]王松桂. 线性模型的理论及其应用[M]. 合肥: 安徽教育出版社, 1987.

[2] 张建军. 线性回归模型系数岭估计的改进研究[J]. 海军工程大学学报, 2005, 17(1): 54～57.

[3] 张建军. 线性回归模型系数Stein估计的改进研究[J]. 海军工程大学学报, 2004, 16(4): 22～25.

[4] Deng W S, Chu C K, Cheng M Y. A study of local ridge regression estimators[J]. Journal of Statistics Planning and Inference, 2001, 93: 225～238.

[5] Wan A T K. On generalized ridge regression estimators under collinearity and balanced loss[J]. Applied Mathematics and Computation, 2002, 129: 455～467.

[6] Hawkins D M, Yin X Y. A faster algorithm for ridge regression of reduced rank data[J]. Computational Statistica amp; Data Analysis, 2002, 40: 253～262.

[7] Ohtani K. Inadimissibility of the Stein-rule estimator under the balanced loss function[J]. Journal of Econometrics, 1999, 88: 193～201.

[8] Hoeral A E, Kennard R W. Ridge regression: biased estimation for non-orthogonal problems[J]. Technometrics, 1970, 12: 55～67.

[9] Stein C M. Multiple regression contributions to probability and statistics[A]. Essays in Honor of Harold Hotelling[C]. Stanford: Stanford University Press, 1960.

[10] Hocking R R, Speed F M, Lynn M J. Aclass of estimators in linear regression[J]. Technometrics, 1976, 18: 425～437.

[11] 凌晨飞. 病态线性回归模型系数的0-k型岭估计[J]. 湖南大学学报, 1990, 17(1): 54～57.

[编辑] 洪云飞

O212

A

1673-1409(2009)02-N019-04

2009-02-27

国家自然科学基金资助项目(60774029); 海军工程大学科学研究基金资助项目(HGDJJ05005, HGDJJ07007)。

杨斌(1968-)，男，1990年大学毕业，硕士，讲师，现主要从事多元统计分析、并行与分布式计算和运筹优化等方面的研究工作。