一种改进的二阶半隐式时间离散格式及稳定性分析

艾莉萍 (长江大学信息与数学学院，湖北 荆州 434023)

一种改进的二阶半隐式时间离散格式及稳定性分析

艾莉萍 (长江大学信息与数学学院，湖北 荆州 434023)

对二阶半隐式时间的离散格式进行了改进，提出了一种可使用较大时间步长的高稳定性格式，并对其稳定性进行了分析。研究结果表明，在经典逼近格式上增加一个与时间离散格式阶数相一致的项可以明显增强计算的稳定性。

二阶半隐式时间离散格式；时间步长；稳定性

分子束外延(Molecular Beam Epitaxy，MBE)是一种新的晶体生长技术[1]。笔者讨论的MBE模型如下：

ht=-δΔ2h-((1-|hx|2)hx)x-((1-|hy|2)hy)y(x,t)∈Ω×(0,T]

(1)

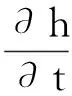
为在数值模拟的过程中使用较大步长，笔者在现有的二阶半离散格式的基础上[2,3]加以改进，给出了高稳定性的二次曲面形式的二阶方法。

1 二阶半隐式时间离散格式

由MBE模型(1)可得如下经典二阶半隐式时间离散格式：

(2)

式中，hn≡hn(x)是h(x,t)在t=tn的逼近；h0(x)由初始条件给出；h1(x)则由一阶方法：

(3)

计算得到。

2 改 进

2.1改进的迭代格式

在经典二阶半隐式时间离散格式中，当δ较小时不能使用较大的时间步长。为提高计算的稳定性，可以构造如下形式的二阶半隐式时间离散格式：

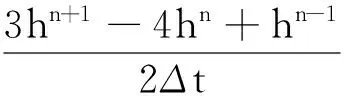
(4)

为方便迭代，将式(4)改写为：

式中，A是一个正数。与经典迭代格式相似，h0(x)由初始条件给出，h1(x)由改进的一阶方法：

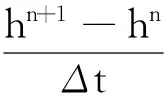
(6)

计算得到。

2.2稳定性分析

为研究算法稳定性，需使用离散能量估计。

引理1[1]若h(x,t)是模型(1)的解，则有如下能量等式成立：

(7)

(8)

式中，‖·‖是Ω上的标准L2范数；‖·‖Lp则是标准Lp范数，且：

(9)

定理1若式(5)中的常数A足够大，则有：

(10)

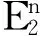
(11)

更进一步还可以得到：

E1(hn)≤E1(h1)+O(Δt)

(12)

式中，E1(h1)由式(9)定义。若式(5)的数值解是收敛的，则在选择A时只需使其满足:

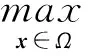
(13)

即可，其中，h(x,t)是模型(1)的解。

证明为表述简便，记δthn=hn+1-hn，δtthn=hn+1-2hn+hn-1，则有：

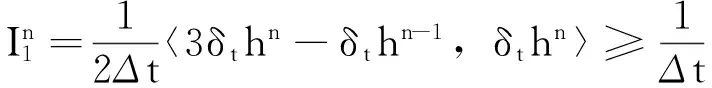
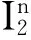
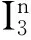
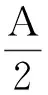
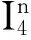
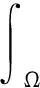
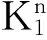
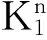
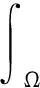
即有：

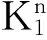
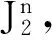
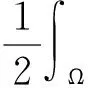
由以上分析可知：

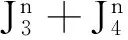
综上所述，有：

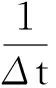
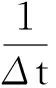
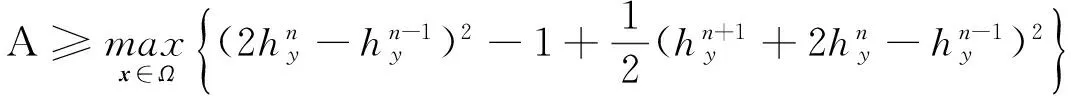
同时成立时，式(10)成立。又由E1的定义式，可得式(12)。

[2]Xu Chuanju, Tang Tao.Stability analysis of large time-stepping methods for epitaxial growth models[J]. SIAM J Numer Anal,2006,(44):1759～1779.

[3]艾莉萍.Cahn-Hilliard方程的大时间步长方法的稳定性分析[D].厦门：厦门大学，2006.

[编辑] 洪云飞

O241.82

A

1673-1409(2009)02-N007-03

2009-02-23

艾莉萍(1983-)，女，2003年大学毕业，硕士，助教，现主要从事偏微分方程数值解方面的教学与研究工作。