持久性有机污染物多氯联苯(PCBs)生物毒性的灰色理论研究

张 旭，谢修银 (长江大学化学与环境工程学院，湖北 荆州 434023)

持久性有机污染物多氯联苯(PCBs)生物毒性的灰色理论研究

张 旭，谢修银 (长江大学化学与环境工程学院，湖北 荆州 434023)

运用灰色理论对10种多氯联苯(PCBs)的生物毒性与其结构参数的定量构效关系进行了研究，建立了其灰色预测模型，通过构建灰色预测模型，计算了各化合物的生物毒性值，并对模型进行了精度检验和分析。研究结果表明，所建立的模型精度为一级(好)，且该模型较一般的线性回归模型具有更好的预测能力，为定量构效关系研究提供了一种新的方法。

持久性有机污染物；多氯联苯(PCBs)；灰色理论；定量构效关系(QSAR)； 生物毒性

持久性有机污染物多氯联苯(Polychlorinated biphenyls，PCBs)是人工合成有机物，PCBs的全部异构体有209个，已确定结构的有102种；PCBs易溶于脂肪、有机溶剂，极难溶于水，极难分解，易在生物体的脂肪内大量富集。全世界已生产和应用的PCBs有1百万吨，其中1/4～1/3已进入人类环境造成公害。1968年，日本发生的米油糠污染就是多氯联苯的污染造成的，PCBs可经皮肤、呼吸道和消化道而被有机体吸收，消化道的吸收率最高。PCBs的毒性因动物种属、健康状况等的不同而异，也与其本身的含氯量、化学结构、各种异构体的混合比以及其他杂质的存在与否而有很大差别。

PCBs在生物体内的降解速率很低，只通过生物降解实验来收集能反映PCBs在生物体内降解转化的速率数据是不容易的。目前的研究重点可以放在降解模型的建立，即利用生物、物理和化学等学科的知识和现代化的模拟、计算手段把一些多变的信息综合成生物降解动力学速率常数，建立有效的生物降解模型。

灰色系统理论用崭新的科学方法对系统信息进行处理、分析和建模。灰色建模方法是通过处理灰信息来揭示事物内部的物征和规律。它利用系统信息，使抽象概念量化，量化的概念模型化，最后进行模型优化。它不但考虑通过输出信息去同构系统模型，同时十分重视关联分析。下面，笔者将运用灰色理论对10种多氯联苯(PCBs)的生物毒性与其结构参数的定量构效关系进行了研究。

1 灰色理论

1.1GM(1,1)模型

GM(1,1)模型是最常用的一种灰色模型，它是由一个只包含单变量的一阶微分方程构成的模型。下面笔者利用连续非等时空距GM(1,1)灰色模型[1,2]来进行建模和预测。具体方法如下：

设自变量x具有指数连接性，原始数据列为：

Y(0)(x)={Y(0)(x1)，Y(0)(x2)，…，Y(0)(xn)} (x=1，2，…，n)

用AGO[3]生成一阶累加生成模块Y(1)(x)：

dY(1)/dx+aY(1)=u

响应方程为：

(1)

式(1)即为GM(1,1)模型灰色预测的具体计算公式。式中的参数a、b、c采用2步最小二乘法即可求出。

1.2模型精度检验

模型精度[4]由后验差比值C和小误差概率P共同确定：

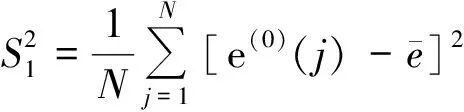
一般将模型精度等级[5～8]分为4级，Ⅰ级最好，Ⅳ级最差。当C≤0.35且P≥0.95时模型精度为Ⅰ级。

2 PCBs生物毒性的研究

2.1数据来源及关联分析

PCBs半效应浓度的负对数(-logEc50)实验数据来源于文献[9]，相关参数logKow(正辛醇/水分配系数)，Vmc/100(分子范德华体积)， π1(极化比率分子)，εB(共价键)，q-(静电碱性电荷)，q+(静电酸性电荷)均来源于文献[10]。相关数据及关联度计算结果见表1。

表1 多氯联苯类化合物的化学结构参数及关联度

从表1很容易看出，表中各化学结构参数与半效应浓度的负对数的关联度大小顺序依次为:

r-logEc50-logKowgt;r-logEc50-Vmc/100gt;r-logEc50-q+gt;r-logEc50-εBgt;r-logEc50-π1gt;r-logEc50-q-

将logKow参数值与-logEc50值作灰色关联分析图，如图1所示。

2.2PCBs实验数据及模型计算结果

利用表1中10种PCBs化合物的-logEc50值与正辛醇/水分配系数的对数值logKow建模得到的系数a的值为0.000147，同时计算出c和b的值为-6072.23和6071.753。

将数据代入式(1)，得：

按模型方程计算得出10种多氯联苯类化合物的-logEc50的计算值、误差和平均值，以及文献的预测值、误差和平均值与实验值的比较列于表2中。-logEc50的实验值、文献预测值与计算值关联分析见图2。

2.3模型精度检验

利用表2中数据计算得S1=0.196028，S2=0.741351，则后验差比值C和小误差频率P为：

C=S1/S2=0.264421lt;0.35

故该模型为Ⅰ级(好)。

注： -logEc50的exp、cal*来源于文献[7] ；cal△为模型计算值。

图1 -logEc50与logKow的关联度分析 图2 -logEc50计算值与实验值、文献值的关联分析

2.4误差分析

根据表2中列出的文献预测值和计算值可得2种方法计算结果的误差，如表3。

表3 多氯联苯类化合物2种方法预测结果误差

由表3可知，笔者所建模型的最大绝对误差、平均绝对误差、最大相对误差、平均相对误差和均方根误差均小于文献[9,10]方法，可见建立的模型明显优于文献方法，具有很好的预测能力。

[1]谢武明，胡勇有，刘焕彬，等.持久性有机污染物的环境问题与研究进展[J].中国环境监测，2004，20(02):58～61.

[2]张素萍，孙兆林.色谱灰色数模的建立及应用研究(Ⅵ)——CGM(1，1，N)模型的建立及烷基苯异构体保留行为的预测[J].高等化学学报，1999，(10):1528～1532.

[3]王岳松，张军，林乐明.苯酚和苯胺类衍生物的结构与薄层色谱保留值关系的研究[J].色谱，1999，17(1):18～20.

[4]张苗云，项成龙.环境预测中灰色模型的Excel解法[J]. 干旱环境监测，2001，15(3)：171～172.

[5]曹军，胡万义.灰色系统理论与方法[M].哈尔滨：东北林业大学出版社，1993.6～44.

[6]傅立.灰色系统理论及其应用[M].北京：科学技术文献出版社，1992.

[7]曾小兰.部分持久性有机污染物的定量结构——性质关系研究[D].桂林：桂林工学院，2007.

[8]张小吐,王朝辉. 非等时空距灰色模型在液相色谱保留值研究中的应用[J].中国国境卫生检疫杂志,1996,19(1):18～21.

[9]Richard D Beger， Dan A Buzatu，Jon G Wilkes. Combining NMR spectral and structural data to form models of polychlorinated dibenzodioxins, dibenzofurans, and biphenyls binding to the AhR[J]. Journal of Computer-Aided Molecular Design,2002,16:727～740.

[10] HUANG Jun, Yu Gang, ZHANG Zu-lin,etal.Application of TLSER method in predicting the aqueous solubility and n-octanol/water partition coefficient of PCBs，PCDDs and PCDFs[J].Journal of Environmental Sciences,2004,16(1):21～29.

[编辑] 洪云飞

O621.13

A

1673-1409(2009)01-N041-03

2008-12-25

张旭(1979-)，男，2001年大学毕业，讲师，硕士生，现主要从事构效学方面的教学与研究工作。